Boost 电路右半平面零点 (RHPZ) 的仿真与解析
在调试 Boost 电路的控制环路时，我们通常会遇到右半平面零点 (RHPZ) 问题，这给环路调试带来很大挑战。RHPZ 对环路会产生 \(90^\circ\) 的相位滞后，常常导致相位裕量不足，成为提升系统性能的主要瓶颈。
1. 右半平面零点 (RHPZ) 来源解析
Boost 电路的传递函数为：
\[\begin{align}
H(s) = \frac{V_g}{D'^2} \frac{D'^2 R - sL}{s^2 LCR + sL + RD'^2} \nonumber
\end{align}
\]
该传递函数的零点位于 \(s = \frac{D'^2 R}{L}\)，由于零点符号为正，因此属于右半平面零点。
为了深入理解右半平面零点的物理起源，我们需要回顾其推导过程。在连续导通模式 (CCM) 下，Boost 电路传递函数的推导基于电感和电容在稳态下的状态方程。在一个开关周期内，根据电感伏秒平衡和电容安秒平衡原理，可列出以下方程：
\[\begin{align}
\langle v_L \rangle &= L\frac{d\langle i_L \rangle}{dt} = d\langle v_g \rangle - (1-d)\langle v_o \rangle \nonumber\\
\langle i_C \rangle &= C\frac{d\langle v_o \rangle}{dt} = (1-d)\langle i_L \rangle - \frac{\langle v_o \rangle}{R} \nonumber
\end{align}
\]
其中：
- \(d\) 是开关管占空比
- \(\langle v_g \rangle\) 是输入电压平均值
- \(\langle v_o \rangle\) 是输出电压平均值
- \(\langle i_L \rangle\) 是电感电流平均值
- \(\langle \cdot \rangle\) 表示一个开关周期内的平均值，即 \(\langle x(t) \rangle = \frac{1}{T_s}\int_{t-T_s}^{t+T_s} x(\tau) d\tau\)
将各平均量分解为直流分量和交流小信号分量：
\[\begin{align}
\langle i_C \rangle &= I_C + \hat{i}_C = \hat{i}_C \nonumber\\
\langle i_L \rangle &= I_L + \hat{i}_L \nonumber\\
\langle v_i \rangle &= V_i + \hat{v}_i \nonumber\\
\langle v_o \rangle &= V_o + \hat{v}_o \nonumber\\
d &= D + \hat{d} \nonumber
\end{align}
\]
将分离后的变量代入状态方程：
\[\begin{align}
L\frac{d\langle i_L \rangle}{dt} &= L\frac{d(I_L + \hat{i}_L)}{dt} = L\frac{d\hat{i}_L}{dt}
= V_i + \hat{v}_i - (1-D-\hat{d})(V_o + \hat{v}_o) \nonumber\\
C\frac{d\langle v_o \rangle}{dt} &= C\frac{d(V_o + \hat{v}_o)}{dt} = C\frac{d\hat{v}_o}{dt}
= (1-D-\hat{d})(I_L + \hat{i}_L) - \frac{V_o + \hat{v}_o}{R} \nonumber
\end{align}
\]
对上述方程进行拉普拉斯变换：
\[\begin{align}
sL\hat{i}_L &= V_g + \hat{v}_i - (1-D-\hat{d})(V_o + \hat{v}_o) \nonumber\\
sC\hat{v}_o &= (1-D-\hat{d})(I_L + \hat{i}_L) - \frac{V_o + \hat{v}_o}{R} \nonumber
\end{align}
\]
将电感方程中的 \(\hat{i}_L\) 代入电容方程，同时忽略直流分量和二阶交流分量，只保留一阶小信号项：
\[\begin{align}
s^2LRC\hat{v}_o + sL\hat{v}_o + (1-D)^2R\hat{v}_o = -sRLI_L\hat{d} - V_iR\hat{d} + (1-D)R\hat{v}_i + 2(1-D)V_oR\hat{d} \nonumber
\end{align}
\]
令 \(\hat{v}_i = 0\)，并利用关系式 \(V_g = (1-D)V_o\) 和 \(I_L = V_o/[R(1-D)]\)，最终化简得到传递函数。
值得注意的是，方程中的 \(-sRLI_L\hat{d}\) 项是右半平面零点的直接来源，这一项是在将电感方程和电容方程联立求解过程中产生的。式电容方程中包含的电感电流与占空比相乘的项 \((1-D-\hat{d})(I_L + \hat{i}_L)\) 是升压型变换器所特有的耦合特性。
因此，所有升压型开关变换器（如 Boost、Flyback、Cuk 等拓扑）都会出现右半平面零点现象。
2. 右半平面零点 (RHPZ) 的仿真验证
在 Python 中，我们可以使用 Matplotlib 绘制传递函数的波特图，并标识出零点位置。假设电感和电容参数固定，通过改变负载电阻 R，观察波特图的变化趋势及零点移动规律。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
from scipy import signal
def bode_plot(tf_list, zero_list, f_min, f_max, ax1=None, ax2=None, colors=None, linestyles=None, labels=None, title=""):
"""
生成伯德图 - 支持多个传递函数，并标出零点位置
参数:
tf_list: 传输函数列表或单个传输函数
zero_list: 零点列表，每个元素对应一个传递函数的零点数组
f_min: 最小频率 (Hz)
f_max: 最大频率 (Hz)
ax1: 幅度图轴对象 (可选)
ax2: 相位图轴对象 (可选)
colors: 颜色列表 (可选)
linestyles: 线条样式列表 (可选)
labels: 标签列表 (可选)
title: 图形标题 (可选)
"""
# 如果输入是单个传递函数，转换为列表
if not isinstance(tf_list, (list, tuple)):
tf_list = [tf_list]
# 如果zero_list不是列表，转换为列表
if not isinstance(zero_list, (list, tuple)):
zero_list = [zero_list]
# 设置默认值
if colors is None:
colors = plt.cm.tab10(np.linspace(0, 1, len(tf_list)))
if linestyles is None:
linestyles = ['-'] * len(tf_list)
if labels is None:
labels = [f'TF {i+1}' for i in range(len(tf_list))]
# 确保列表长度一致
if len(colors) < len(tf_list):
colors = colors * (len(tf_list) // len(colors) + 1)
if len(linestyles) < len(tf_list):
linestyles = linestyles * (len(tf_list) // len(linestyles) + 1)
if len(labels) < len(tf_list):
labels = labels + [f'TF {i+1}' for i in range(len(labels), len(tf_list))]
# 确保zero_list长度与tf_list一致
if len(zero_list) < len(tf_list):
# 如果零点列表较短，用空列表填充
zero_list = list(zero_list) + [[] for _ in range(len(zero_list), len(tf_list))]
# 如果没有提供轴对象，则创建新的图形
if ax1 is None or ax2 is None:
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8))
show_plot = True
else:
show_plot = False
# 为每个传递函数生成Bode图
for i, tf in enumerate(tf_list):
frequencies = np.logspace(np.log10(f_min), np.log10(f_max), 1000)
omega = 2 * np.pi * frequencies
w, mag, phase = signal.bode(tf, omega)
# 绘图参数
color = colors[i] if i < len(colors) else None
linestyle = linestyles[i] if i < len(linestyles) else '-'
label = f'R={labels[i]}' if i < len(labels) else f'TF {i+1}'
# 幅度图
line_mag = ax1.semilogx(w, mag, color=color, linestyle=linestyle, label=label, linewidth=2)
ax1.set_ylabel('幅度 (dB)')
ax1.grid(True, which="both", ls="-", alpha=0.3)
# 相位图
line_phase = ax2.semilogx(w, phase, color=color, linestyle=linestyle, label=label, linewidth=2)
ax2.set_xlabel('角频率 (Rad/s)')
ax2.set_ylabel('相位 (Degree)')
ax2.grid(True, which="both", ls="-", alpha=0.3)
# 标记零点位置
if i < len(zero_list) and zero_list[i] is not None:
zeros = zero_list[i]
# 确保zeros是数组形式
if not isinstance(zeros, (list, tuple, np.ndarray)):
zeros = [zeros]
for zero in zeros:
# 只在频率范围内标记零点
if f_min <= zero/(2*np.pi) <= f_max:
# 获取当前线条的颜色
line_color = line_mag[0].get_color()
# 在零点频率处计算传递函数值
w_zero = zero # 零点的角频率
s_zero = 1j * w_zero
# 近似计算零点处的响应值（简化处理）
try:
# 使用频率响应计算零点处的近似值
_, mag_zero, phase_zero = signal.bode(tf, [w_zero])
if phase_zero[0] < -360:
phase_zero[0] += 360
elif phase_zero[0] > 0:
phase_zero[0] -= 360
# 在图上标记零点
ax1.plot(w_zero, mag_zero[0], 'o', color=line_color, markersize=6,
markeredgecolor='black', markeredgewidth=1)
ax2.plot(w_zero, phase_zero[0], 'o', color=line_color, markersize=6,
markeredgecolor='black', markeredgewidth=1)
# 添加垂直虚线指示零点位置
ax1.axvline(w_zero, color=line_color, linestyle=':', alpha=0.7)
ax2.axvline(w_zero, color=line_color, linestyle=':', alpha=0.7)
except:
# 如果计算失败，至少画一条垂直线表示零点位置
ax1.axvline(w_zero, color=line_color, linestyle=':', alpha=0.7)
ax2.axvline(w_zero, color=line_color, linestyle=':', alpha=0.7)
# 设置标题和图例
if show_plot:
if title:
plt.suptitle(title)
ax1.legend()
ax2.legend()
plt.tight_layout()
plt.show()
return ax1, ax2
# 使用典型升压转换器值的示例
if __name__ == "__main__":
# 典型升压转换器参数
L = 300e-6 # 300 μH
C = 100e-6 # 100 μF
r_L = 0.01 # 10 mΩ 电感电阻
r_C = 0.05 # 50 mΩ 电容ESR
V_in = 20 # 20 V 输入
V_out = 40 # 40 V 输出
f_min = 10
f_max = 1e6
# 不同负载电阻值
R_values = [0.5, 10, 200, 5000] # 不同的负载电阻值
# 计算占空比
D = 1-V_in/V_out
# 计算不同负载电阻的零点及传递函数
zeros = []
tf_list = []
for R in R_values:
num = [-L*V_in/((1-D)**2), R*V_in]
den = [L*R*C, L, R*(1-D)**2]
tf = signal.TransferFunction(num, den)
tf_list.append(tf)
zero = (1-D)**2*R/L
zeros.append(zero)
# 定义颜色和线型
colors = ['blue', 'red', 'green', 'orange']
linestyles = ['-', '--', '-.', ':']
# 创建图形和轴
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 10))
result = bode_plot(tf_list, zeros, f_min, f_max,
ax1, ax2, colors, linestyles, R_values, 'Boost 电路不同负载电阻下的 Bode 图')
# 添加图例
ax1.set_ylabel('幅值 (dB)', fontsize=12)
ax1.set_title('Boost 电路不同负载电阻下的 Bode 图', fontsize=14)
ax1.legend()
ax1.grid(True, which="both", ls="-", alpha=0.3)
ax2.set_xlabel('角频率 (Rad/s)', fontsize=12)
ax2.set_ylabel('相位 (度)', fontsize=12)
ax2.legend()
ax2.grid(True, which="both", ls="-", alpha=0.3)
plt.tight_layout()
plt.show()
运行脚本，将生成以下结果：
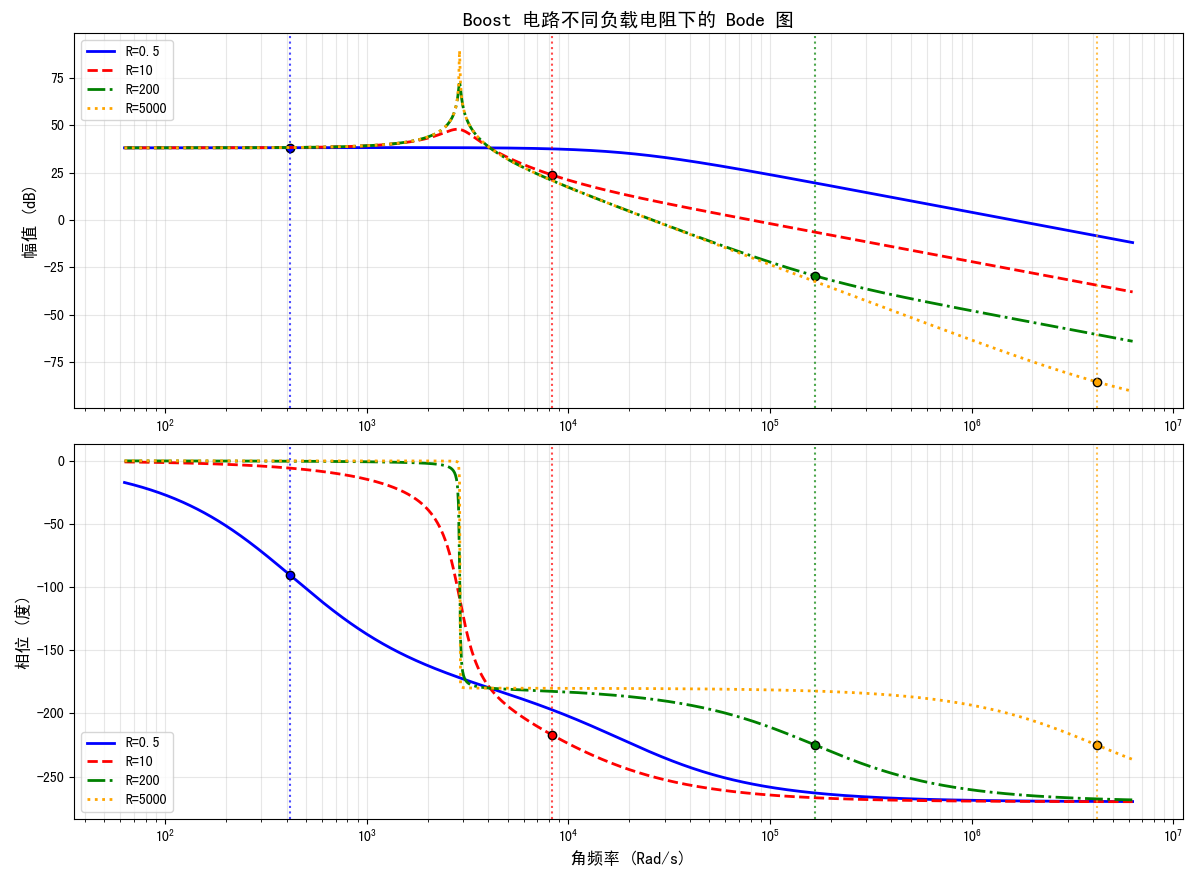
从仿真结果可以看出，当负载电阻减小时，右半平面零点向低频方向移动。由于右半平面零点会产生 \(90^\circ\) 的相位滞后，当其处于较低频率时，会给补偿器设计带来很大困难。
3. 右半平面零点 (RHPZ) 的补偿策略
通常的解决方法是降低补偿器增益，使穿越频率位于零点频率之前。但这会导致系统带宽变窄，影响动态响应速度。
通过适当调整补偿器的零极点位置可以在一定程度上缓解这个问题。例如，采用包含 1 个零点和 2 个极点的补偿器，其传递函数为：
\[G(s) = 110 \cdot \frac{s + 50}{s \cdot (s + 10000)}
\]
该补偿器的设计考虑：
- 分母中的单独 \(s\) 项提供积分作用，确保直流增益足够高，以减小稳态误差
- 积分器本身带来 \(90^\circ\) 相位滞后，加上 RHPZ 的 \(90^\circ\) 滞后，需要在低频处添加左半平面零点来提供相位超前
- 第二个极点设置在适当频率，用于限制高频增益，防止噪声放大
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
def bode_plot(tf_list, f_min, f_max, ax1=None, ax2=None, colors=None, linestyles=None, labels=None, title=""):
"""
生成伯德图 - 支持多个传递函数
参数:
tf_list: 传输函数列表或单个传输函数
f_min: 最小频率 (Hz)
f_max: 最大频率 (Hz)
ax1: 幅度图轴对象 (可选)
ax2: 相位图轴对象 (可选)
colors: 颜色列表 (可选)
linestyles: 线条样式列表 (可选)
labels: 标签列表 (可选)
title: 图形标题 (可选)
"""
# 如果输入是单个传递函数，转换为列表
if not isinstance(tf_list, (list, tuple)):
tf_list = [tf_list]
# 设置默认值
if colors is None:
colors = plt.cm.tab10(np.linspace(0, 1, len(tf_list)))
if linestyles is None:
linestyles = ['-'] * len(tf_list)
if labels is None:
labels = [f'TF {i+1}' for i in range(len(tf_list))]
# 确保列表长度一致
if len(colors) < len(tf_list):
colors = colors * (len(tf_list) // len(colors) + 1)
if len(linestyles) < len(tf_list):
linestyles = linestyles * (len(tf_list) // len(linestyles) + 1)
if len(labels) < len(tf_list):
labels = labels + [f'TF {i+1}' for i in range(len(labels), len(tf_list))]
# 如果没有提供轴对象，则创建新的图形
if ax1 is None or ax2 is None:
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8))
show_plot = True
else:
show_plot = False
# 为每个传递函数生成Bode图
for i, tf in enumerate(tf_list):
frequencies = np.logspace(np.log10(f_min), np.log10(f_max), 1000)
omega = 2 * np.pi * frequencies
w, mag, phase = signal.bode(tf, omega)
# 绘图参数
color = colors[i] if i < len(colors) else None
linestyle = linestyles[i] if i < len(linestyles) else '-'
label = labels[i] if i < len(labels) else f'TF {i+1}'
# 幅度图
ax1.semilogx(w, mag, color=color, linestyle=linestyle, label=label)
ax1.set_ylabel('幅度 (dB)')
ax1.grid(True, which="both", ls="-", alpha=0.3)
# 相位图
ax2.semilogx(w, phase, color=color, linestyle=linestyle, label=label)
ax2.set_xlabel('角频率 (Rad/s)')
ax2.set_ylabel('相位 (Degree)')
ax2.grid(True, which="both", ls="-", alpha=0.3)
# 设置标题和图例
if show_plot:
if title:
plt.suptitle(title)
ax1.legend()
ax2.legend()
plt.tight_layout()
plt.show()
return ax1, ax2
def series_transfer_functions(tf1, tf2):
"""
将两个传递函数串联
参数:
tf1: 第一个传递函数 (TransferFunction对象)
tf2: 第二个传递函数 (TransferFunction对象)
返回:
串联后的传递函数
"""
# 串联传递函数：H(s) = H1(s) * H2(s)
# 分子：num = conv(num1, num2)
# 分母：den = conv(den1, den2)
num_result = np.convolve(tf1.num, tf2.num)
den_result = np.convolve(tf1.den, tf2.den)
return signal.TransferFunction(num_result, den_result)
def safe_vector_add_right(vec1, vec2):
"""Right-aligned vector addition using basic loops"""
len1 = len(vec1)
len2 = len(vec2)
if len1 >= len2:
# vec1 is longer
result = []
# Copy the beginning of vec1 that doesn't overlap
for i in range(len1 - len2):
result.append(vec1[i])
# Add the overlapping parts
for i in range(len2):
result.append(vec1[len1 - len2 + i] + vec2[i])
else:
# vec2 is longer
result = []
# Copy the beginning of vec2 that doesn't overlap
for i in range(len2 - len1):
result.append(vec2[i])
# Add the overlapping parts
for i in range(len1):
result.append(vec1[i] + vec2[len2 - len1 + i])
return result
def close_loop_transfer_function(tf):
"""
计算闭环传输函数
参数:
tf: 传递函数 (TransferFunction对象)
返回:
闭环传输函数
"""
return signal.TransferFunction(tf.num, safe_vector_add_right(tf.den, tf.num))
if __name__ == "__main__":
# 输入参数
L = 300e-6 # 300 μH
C = 100e-6 # 100 μF
R = 0.5
V_in = 20 # 20 V 输入
V_out = 40 # 40 V 输出
f_min = 1
f_max = 1e6
# 创建多个传递函数
D = 1 - V_in/V_out
# Boost传递函数
num1 = [-L*V_in/((1-D)**2), R*V_in]
den1 = [L*R*C, L, R*(1-D)**2]
boost_tf = signal.TransferFunction(num1, den1)
# 补偿器的传递函数
gain = 110
zeros = [-50]
poles = [0, -10000]
num2 = np.array(np.poly(zeros))*gain
den2 = np.poly(poles)
comp_tf = signal.TransferFunction(num2, den2)
# 补偿后的Boost传递函数
boost_comp_tf = series_transfer_functions(boost_tf, comp_tf)
# 闭环传输函数
close_tf = close_loop_transfer_function(boost_comp_tf)
# 传递函数列表
tf_list = [boost_tf, comp_tf, boost_comp_tf, close_tf]
labels = ['补偿前的Boost', '补偿器', '补偿后的Boost', '闭环传递函数']
colors = ['blue', 'red', 'green', 'black']
linestyles = ['-', '--', '-.', ':']
# 绘制所有传递函数
bode_plot(tf_list, f_min, f_max, colors=colors, linestyles=linestyles,
labels=labels, title="Boost 电路补偿前后的Bode图对比")
仿真结果如图所示：
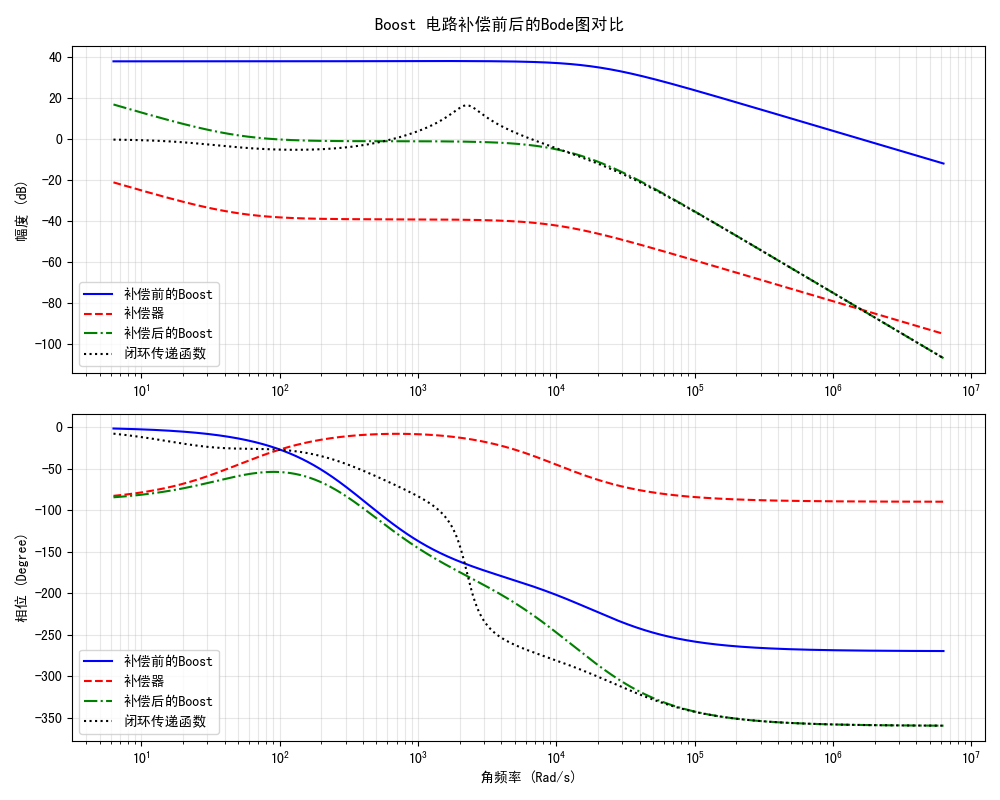
从图中可以看出，补偿后的环路带宽约为 1000 rad/s，穿越频率对应的相位约为 \(-150^\circ\)，相位裕量约 \(30^\circ\)，环路基本稳定。
然而，这种补偿方案存在局限性。当负载电阻增大至 \(R = 50\Omega\) 时，重新仿真得到如下结果：
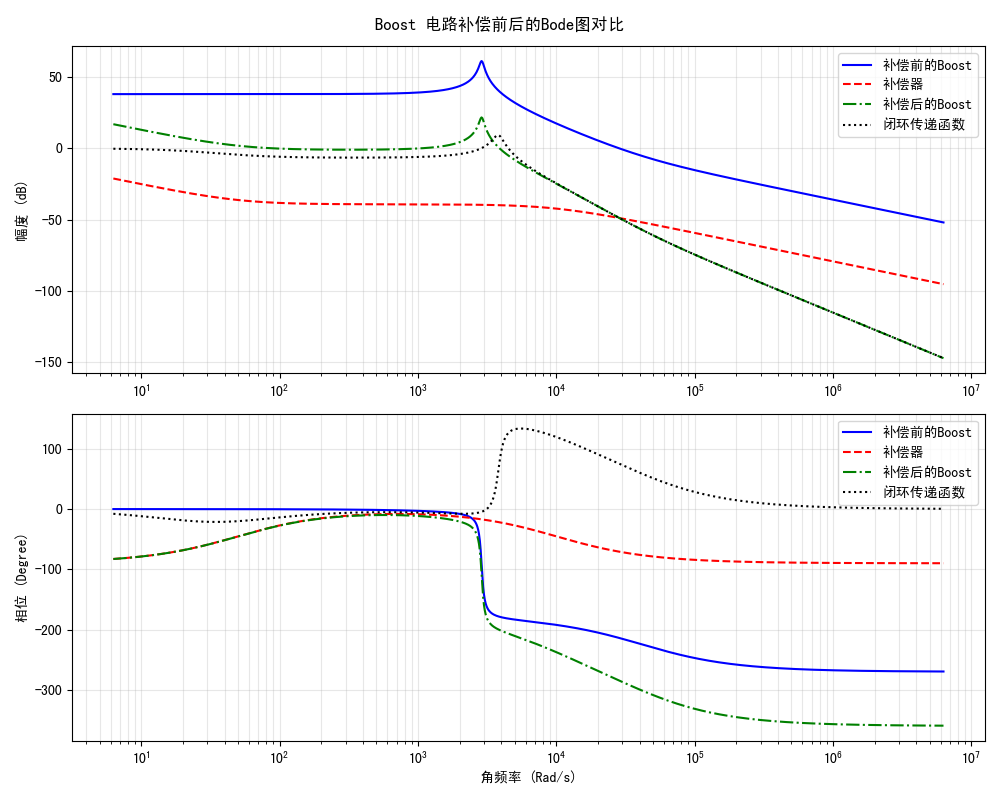
此时补偿后的穿越频率对应相位降至 \(-200^\circ\) 以下，环路变得不稳定。原因在于当 R 增大时，Boost 电路的两个共轭极点向 LC 谐振频率靠拢，在两个极点各 \(-90^\circ\) 相位滞后的叠加作用下，环路相位在该频率处急剧下降 \(180^\circ\)，导致系统失稳。
4. 结论与讨论
-
RHPZ 的本质：右半平面零点是升压型变换器的固有特性，源于电感电流与占空比之间的非线性耦合关系。
-
负载依赖性：RHPZ 的位置随负载电阻变化，轻载时向低频移动，给环路稳定性设计带来更大挑战。
-
补偿局限性：
- 固定参数的补偿器难以在宽负载范围内保证稳定性
- 为规避 RHPZ 的影响，通常需要限制带宽，但这会牺牲动态性能
- 相位裕量有限，常规补偿方法难以突破带宽限制
-
改进方向：
- 采用自适应补偿策略，根据负载变化调整补偿器参数
- 引入前馈控制等先进控制技术
- 在系统设计时充分考虑工作负载范围，优化参数折衷
右半平面零点的存在从根本上限制了 Boost 变换器的动态性能，在实际工程中需要在稳定性、带宽和负载适应性之间进行仔细权衡。
浙公网安备 33010602011771号