使用 GeckoCircuits 设计 Buck 电源环路

使用 GeckoCircuits 设计 Buck 电源环路

笔者最近发现一款开源的电力电子仿真软件 GeckoCircuits，它是由苏黎世联邦理工学院（ETH）开发的，具有极高的仿真速度，软件小巧，功能强大。本文尝试用这款软件仿真一下 Buck 电路及其控制环路。

电路搭建

• 打开 GeckoCircuits，这是软件的主界面。

• 从软件界面右侧的工具栏中找到 Circuit 元件组，使用里面的电路元件搭建 Buck 电路。

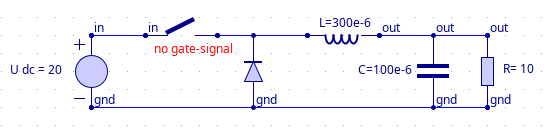
• 电路参数设置：

\[U_{dc}=20V \\ L=300\mu H \\ C=100\mu F \\ R=10\Omega \]

• 注意开关下方显示 "no gate-signal"，那么接下来需要添加对应的信号源。

设置信号源

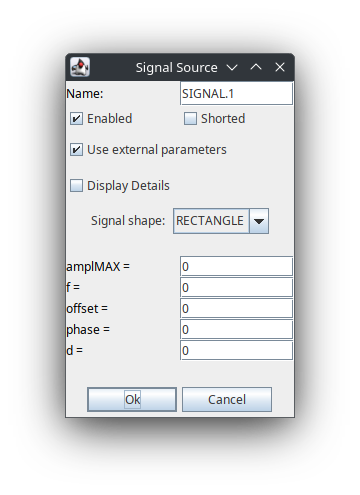
• 找到 Signal/Sink 元件组，使用 Signal Source 作为开关的信号源。波形选择方波 (RECTANGLE)，最大幅度值 (amplMAX)、频率 (f)、占空比 (d) 等参数先不填写，勾选 "Use external parameters"，这样方便将参数连接到控制器。

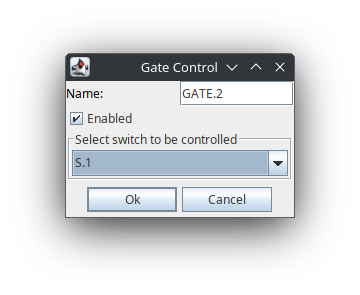
• 放置 Gate Control 元件，在属性菜单中选择开关元件的标号，这样就将栅极驱动信号连接到了开关上。

• 放置 Constant Value 元件，设置数值并连接到信号源参数的输入。参数设置：

\[amplMAX=1 \\ f=50e3 \\ offset=0 \\ phase=0 \\ duty=0.5 \]

• 这时的信号连接图：

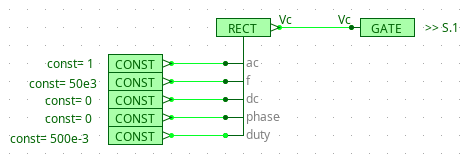
小信号分析

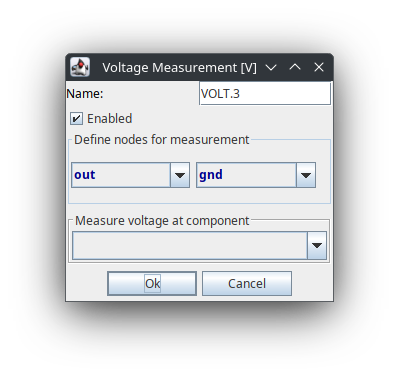
• 找到 Measure 元件组，放置 Voltage Measurement 元件，设置需要测量电压的网络名称：

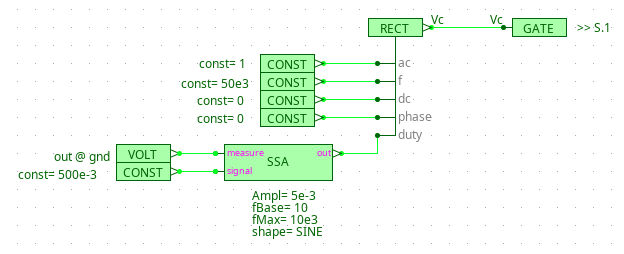
• 找到 Special 元件组，放置 Small Signal Analysis (SSA) 元件，对该电路传递函数 \(G_{vd}(s)\)（即输出电压对占空比的传递函数）进行小信号分析。
• signal 连接大信号（一个固定占空比数值 0.5），out 连接需要被扰动的对象 duty，measure 连接输出信号 \(V_{out}\)：

• SSA 参数设置：

\[Ampl=20e-3 \\ f_{Base}=10 \\ f_{Max}=10e3 \]

意思是对比占空比施加 2% 的扰动，扰动起始频率为 10Hz，最大频率为 10000 Hz。扰动幅度值需要反复调试，该值过大或过小都可能导致结果不准确。

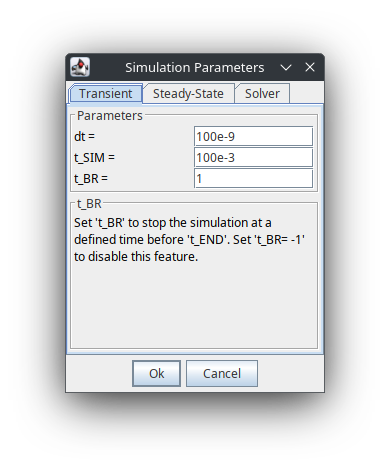
• 按 F5 设置仿真参数：
  仿真步距 (dt) 为 100 ns，仿真时长 (t_SIM) 为 100 ms，仿真断点 (t_BR) 暂不使用。

• 按 F1 运行仿真，仿真结束时菜单栏会有 "stopped after xxxx[s]" 的提示，双击 SSA 元件，查看分析结果。

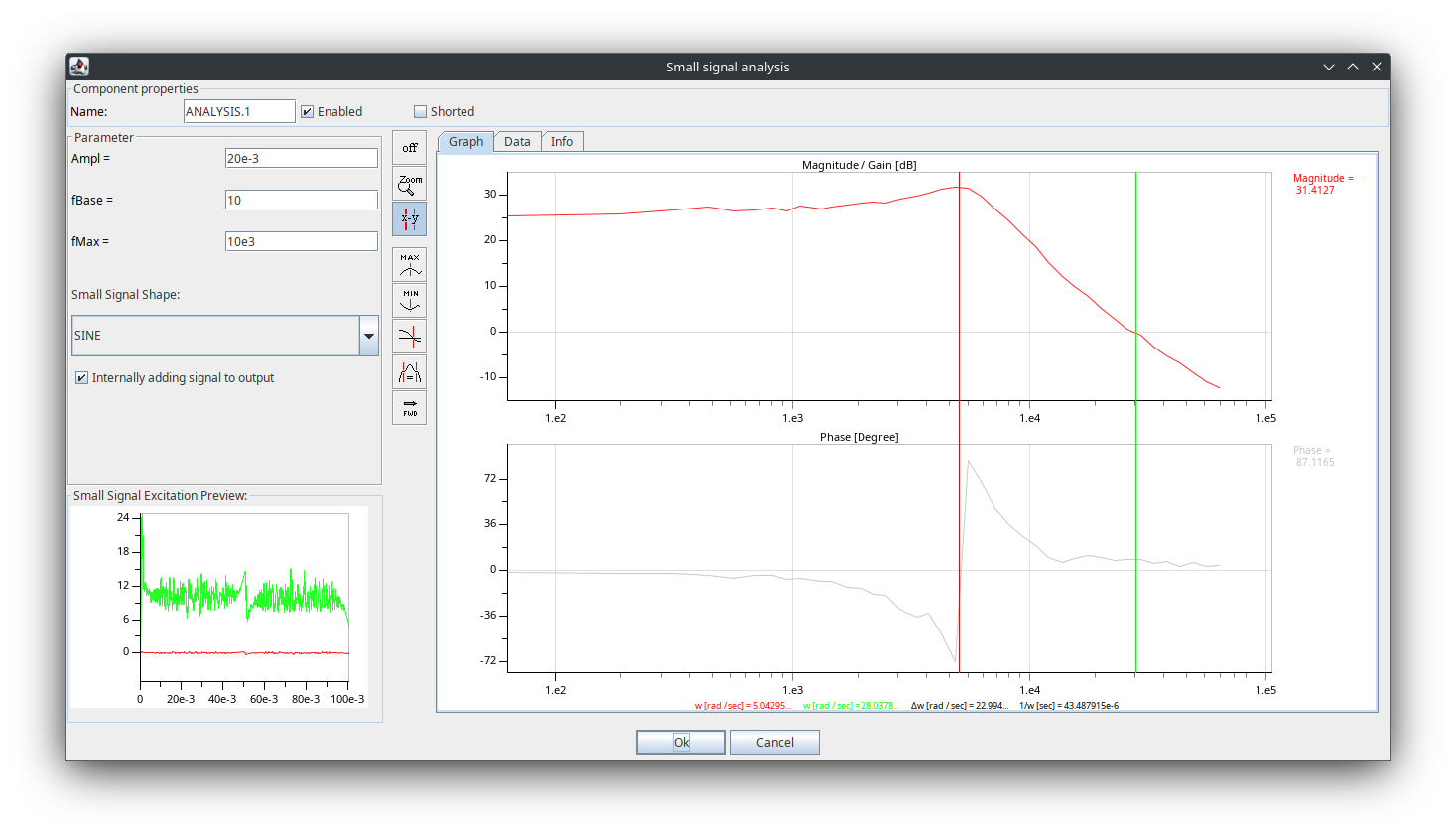
• 下面用理论值验证分析结果，Buck 电路的传递函数为：

\[G_{vd}(s) = \frac{\hat{V}_{out}}{\hat{d}} = \frac{R \cdot D \cdot V_{in}}{s^2 \cdot R \cdot L \cdot C + s \cdot L + R} \]

在 Python 中使用 scipy.signal.lti 模块绘制该函数，并与 SSA 输出的 Bode 图进行对比：

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# Buck转换器参数
Vin = 20.0        # 输入电压 (V)
Vout = 10.0       # 输出电压 (V)
f_sw = 50e3       # 开关频率 (Hz)
L = 300e-6        # 电感值 (H)
C = 100e-6        # 电容值 (F)
ESR = 0           # 电容的等效串联电阻 (欧姆)
RL = 10.0         # 负载电阻 (欧姆)

# 占空比
D = Vout / Vin

# 定义Buck转换器的传递函数
# 使用小信号模型:
# Gvd(s) = Vout(s)/D(s)，其中Vin为常数

# 传递函数的系数
# 分子: [D * Vin]
# 分母: [L*C, L/RL + ESR*C, 1]

num = [D * Vin]
den = [L*C, L/RL + ESR*C, 1]

# 创建传递函数
buck_tf = signal.TransferFunction(num, den)

# 生成Bode图的频率范围
frequencies = np.logspace(1, 7, 1000)  # 10 Hz 到 10 MHz
omega = 2 * np.pi * frequencies

# 生成Bode图
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8))

# 获取Bode图数据
w, mag, phase = signal.bode(buck_tf, omega)

# 幅度图
ax1.semilogx(w, mag)
ax1.set_ylabel('(dB)')
ax1.set_title('')
ax1.grid(True, which="both", ls="-", alpha=0.3)

# 相位图
ax2.semilogx(w, phase)
ax2.set_xlabel('(Rad/s)')
ax2.set_ylabel('(Degree)')
ax2.grid(True, which="both", ls="-", alpha=0.3)

plt.tight_layout()
plt.show()

# 计算附加参数
# 零频率幅度 (在 ω = 0 处)
zero_freq_mag = 20 * np.log10(abs(D * Vin))

# 谐振频率 (无阻尼自然频率)
omega_n = 1 / np.sqrt(L * C)
f_res = omega_n / (2 * np.pi)

# 穿越频率 (幅度为 0 dB 处的频率)
# 查找幅度穿越 0 dB 的频率
# 通过插值找到更精确的穿越频率
mag_linear = 10**(mag/20)
mag_diff = mag_linear - 1  # 与 1 (0 dB) 的差值
# 查找符号变化的位置
idx = np.where(np.diff(np.sign(mag_diff)))[0]

if len(idx) > 0:
    # 线性插值找到更精确的穿越频率
    i = idx[0]
    freq1, freq2 = w[i], w[i+1]
    mag1, mag2 = mag_linear[i], mag_linear[i+1]
    # 线性插值计算穿越频率
    cross_freq = freq1 + (freq2 - freq1) * (1 - mag1) / (mag2 - mag1)
else:
    cross_freq = None

# 打印传递函数详情
print(f"Buck转换器传递函数:")
print(f"占空比 (D) = {D:.2f}")
print(f"传递函数: {num[0]:.2f} / ({den[0]:.2e}s^2 + {den[1]:.2e}s + 1)")
print(f"零频率幅度: {zero_freq_mag:.2f} dB")
print(f"谐振频率: {f_res:.2f} Hz ({omega_n:.2f} 弧度/秒)")
if cross_freq is not None:
    print(f"穿越频率: {cross_freq:.2f} 弧度/秒 ({cross_freq/(2*np.pi):.2f} Hz)")
else:
    print("穿越频率: 在频率范围内未找到")

Python 输出结果如下：

Buck转换器传递函数:
占空比 (D) = 0.50
传递函数: 10.00 / (3.00e-08s^2 + 3.00e-05s + 1)
零频率幅度: 20.00 dB
谐振频率: 918.88 Hz (5773.50 弧度/秒)
穿越频率: 19135.73 弧度/秒 (3045.55 Hz)

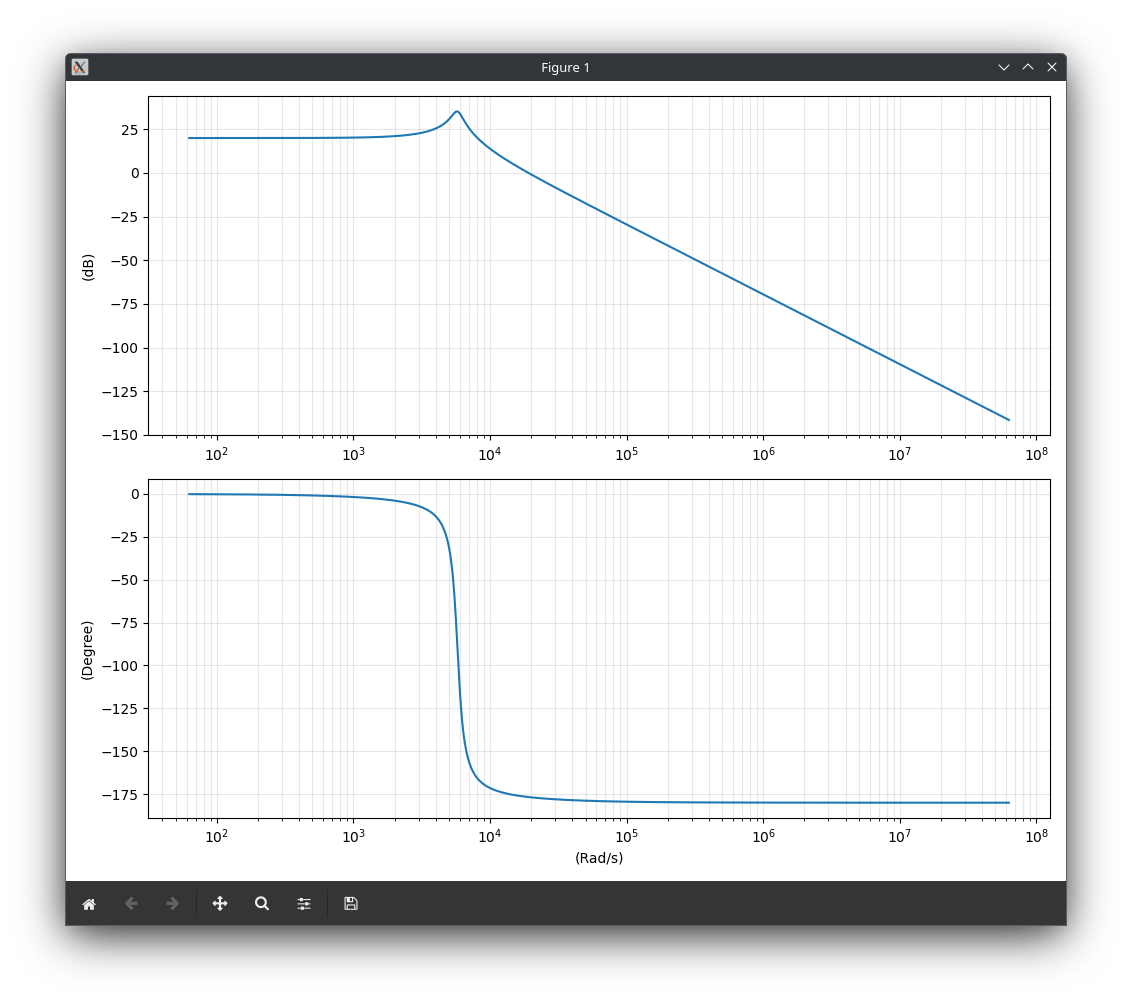
与理论值相比较，SSA 生成的 Bode 图在零频处增益约为 25 dB，谐振频率约为 5000 rad/s，穿越频率约为 28000 rad/s。波形与理论值接近。

控制器设计

• 搭建一个电压反馈环路，环路设定值为 10 V，控制器使用 2P1Z 补偿器。信号连接如下图：

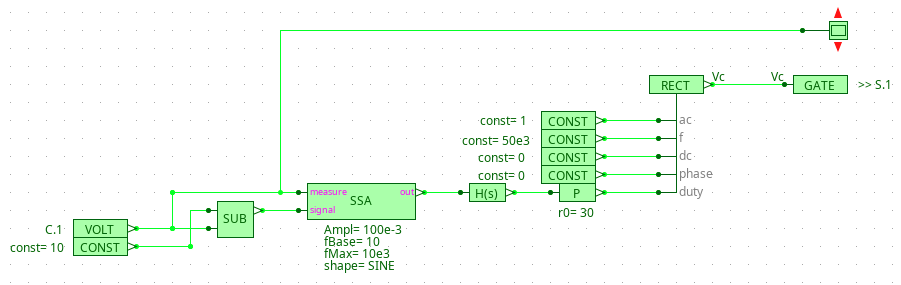
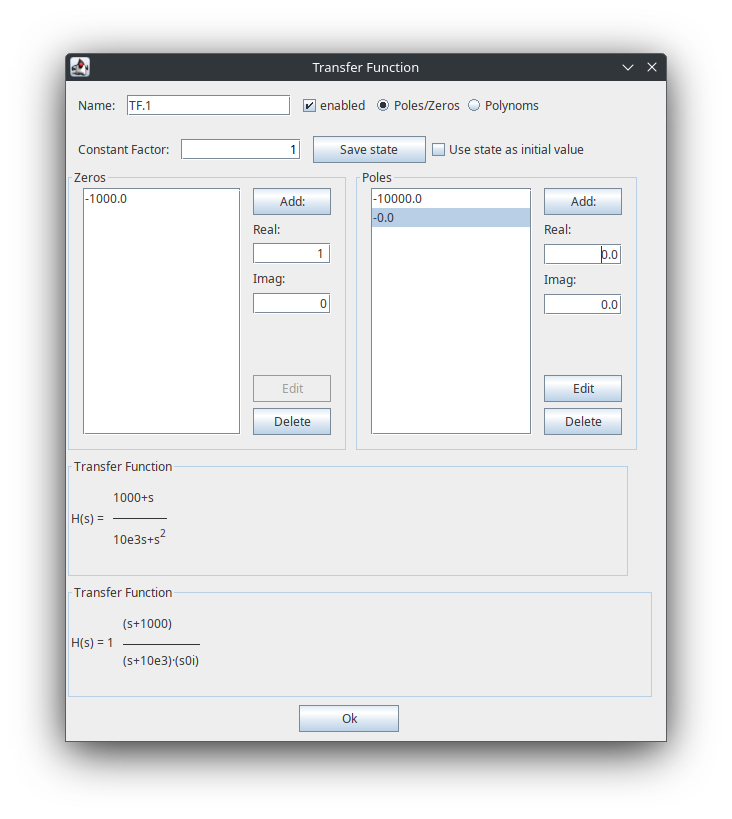
解释一下其中用到的模块：SUB 是减法器，用于计算输出电压与环路设定值之间的差。右上角带红色箭头的元件是波形查看器 (Scope)，它被连接到电压测量器上用于查看输出电压。H(S) 是传递函数模块，P 是增益模块 (GAIN)，其实也属于传递函数的一部分，单独用来设置增益。P 模块设置为 30，H(S) 模块设置两个极点一个零点：

SSA 模块放置在 SUB 和 H(S) 模块之间，用于分析补偿后的开环传递函数：

\[H(s)*G_{vd}(s)=\frac{\hat{V}_{out}}{\hat{V}_e} \]

• 然后运行仿真，查看 SSA 生成的结果。

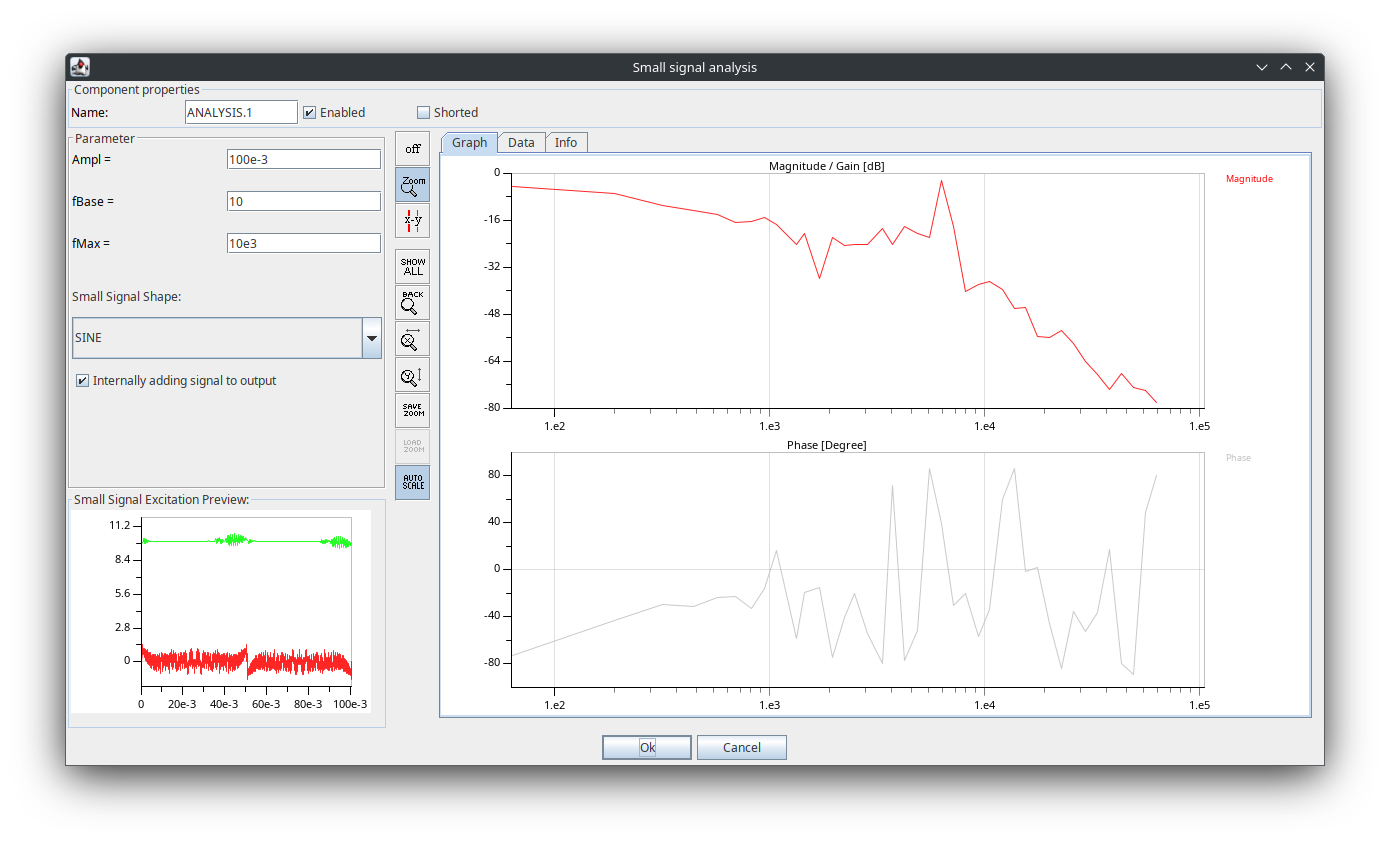
在 6000 rad/s 处增益值有一个尖峰，这是 Buck 电路的谐振峰，它的位置和补偿前没太大变化。在高频处，相位值反复上下跳动，这在理论值波形中并没有这个现象。其实这是由于软件相位值的显示刻度不能缩放，显示范围有限，超出范围的部分会跳变到另一端。

查看时域波形

• 将 SSA 模块去掉，将 SUB 直接和 H(S) 连接，再次运行仿真。点开 Scope 模块，查看时域波形：

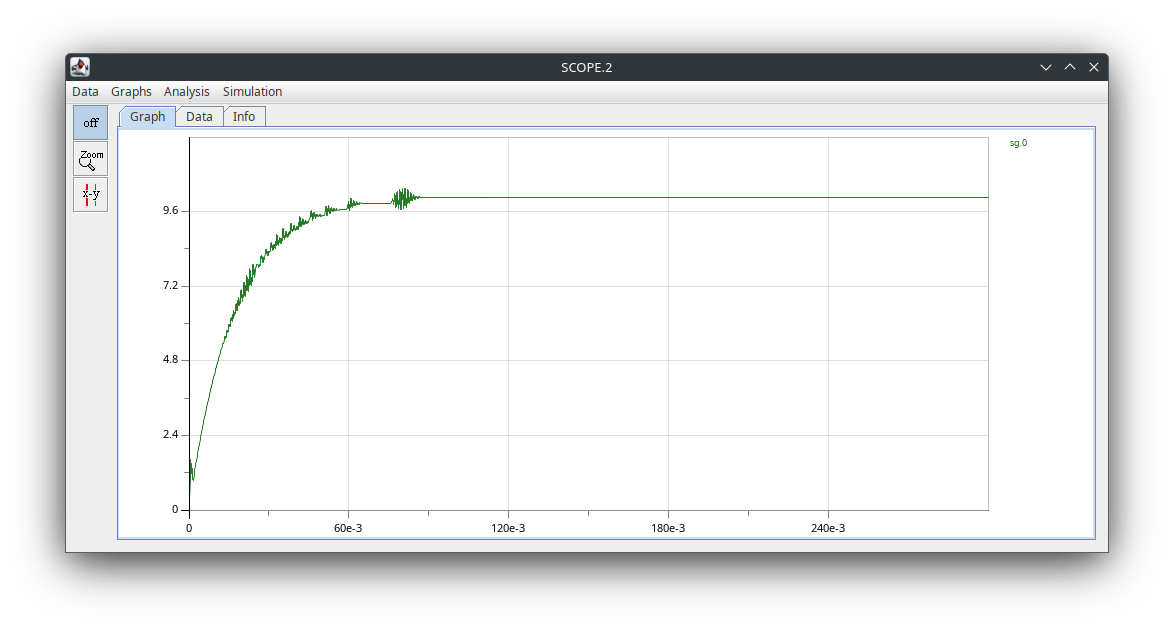
总结

这款软件使用起来总体感觉是非常流畅的，软件的 UI 界面非常简洁和美观。软件是用 Java 语言写的,需要运行在 JVM 上，这点需要注意。不足点的话，SSA 模块有些 bug，比如运行时，如果设置的参数有误，比如设置的仿真时间低于了最低的扫频频率，那么运行完之后，这个模块就点不进去了，只能删掉重新放置一个。此外，软件还可以磁仿真、热仿真，自定义模块可以嵌入 C/C++, Java 等语言,可以说功能十分强大，后续使用之后再来分享。