Jijidawang

小题狂练 (H)

\[\newcommand{\lcp}{\operatorname{lcp}}\newcommand{\lcs}{\operatorname{lcs}}\newcommand{\suf}{\operatorname{suf}}\newcommand{\dist}{\operatorname{dist}}\newcommand{\dep}{\operatorname{dep}}\newcommand{\mxd}{\operatorname{mxd}}\newcommand{\ord}{\operatorname{ord}}\newcommand{\lcm}{\operatorname{lcm}}\newcommand{\FWT}{\operatorname{FWT}}\newcommand{\popcount}{\operatorname{popcount}} \]

目录

目录

[湖北省选模拟 2023] 日记 / diary

考虑对于每个 \(R=P+Q\) 只在最后的分割点处统计其贡献：对于 \(L=|\lcp(R,S)|\)，取 \(P=S[1:L]\)，接下来 \(Q\) 需要满足 \(Q_1\neq S_{L+1}\) .

令 \(f(i,j)\) 表示不考虑 \(T\) 的限制的情况下，满足 \(|P|\le i\) 且 \(|Q|\le n-j+1\) 的 \((P,Q)\) 数量 . 计算 \(c,d\) 表示 \(T\) 在 \(S\) 中第一次出现的开头和在 \(S\) 中最后一次出现的结尾 . 可以先拿 \(f(n,1)-f(c-1,d+1)\) 估计答案，这样会导致少算存在 \(|P|<c\) 且 \(|Q|<n-d+1\) 的分割的包含 \(T\) 的 \(R\) .

让 \(c\) 减一、\(d\) 加一，那么问题转为计算 \(P\) 的结束位置在 \(c\) 左侧且 \(Q\) 的开始位置在 \(d\) 右侧的 \(R\supseteq T\) 的数量 .

考虑从 \(R\) 中删去 \(T\) . 令这样操作后 \(P,Q\) 变为了 \(P',Q'\)，枚举 \(L=|P'|\)，那么 \(|Q'|\) 需要满足 \(|\lcs(S[d:n-|Q'|],T)|\ge m-|\lcp(S[L+1:c],T)|\) .

考虑在最小的 \(|P'|\) 处统计贡献 . 这意味着不存在合法的 \(P'',Q''\) 使得 \(P''+T+Q''=P'+T+Q'\) 且 \(|P''|<|P'|\) . 考察两对字符串 \((P'_1,Q'_1),(P'_2,Q'_2)\) 满足 \(R=P'_1+T+Q'_1=P'_2+T+Q'_2\) 且 \(|P'_1|<|P'_2|\)，那么 \((P'_2,Q'_2)\) 不应被计算 . 令 \(p=|P'_2|-|P'_1|\le m\)，则：

  • 由 \(P'_1+T+Q'_1=P'_2+T+Q'_2\)，可知 \(\suf(P'_2,p)=T[1:p]\) 且 \(Q'_2[1:p]=\suf(T,p)\) . 由于 \(Q'_2\) 的开始位置在 \(d\) 右侧，从而第二条限制可以转写为 \(|\lcp(S[d:n-|Q'_2|])|\ge p\) .
  • 令 \(R=P'_1+T'+Q'_2\)，则 \(|T'|=m+p\) 且 \(T\) 是 \(T'\) 的 border，那么 \(p\) 是 \(T'\) 的 period，进而可以导出 \(p\) 是 \(T\) 的 period .

那么可以导出舍去 \((P',Q')\) 的充要条件（充分性易证）为存在 \(p\) 使得：

  • \(p\) 是 \(T\) 的 period .
  • \(\suf(P',p)=T[1:p]\) .
  • \(|\lcp(S[d:n-|Q'_2|])|\ge p\) .

枚举 \(|P'|\)，在 fail 树上预处理出对应的最小的 \(p\)，接下来对 \(Q'\) 的限制可以由 exKMP 刻画 . 最后限制是一个区间的形式，整个问题可以以 \(O(n+m)\) 的时间复杂度解决 .

[ARC125E] Snack

首先有一个网络流的模型：\(n\) 个左部点 \(u_{1\dots n}\)、\(m\) 个右部点 \(v_{1\dots m}\)，连 \(S\to u_i\) 容量为 \(a_i\)、\(u_i\to v_j\) 容量为 \(b_j\)、\(v_i\to T\) 容量为 \(c_i\)，最大流即为答案 .

那么大概是一个 Gale-Ryser 定理状物 . 首先转成最小割，假设 \(k\) 个左部点连 \(S\)，则每个右部点连 \(S\) 的代价为 \(c_i\)、连 \(T\) 的代价为 \(k\cdot b_i\)，从而可以简单写出答案的表达式：

\[\mathrm{ans}=\min_k\left\{\sum_{i=1}^ka_i+\sum_{i=1}^m\min(c_i,(n-k)b_i)\right\} \]

其中 \(a\) 序列按从小到大排序 . 那么可以简单通过使用双指针在线性对数时间复杂度内计算 .

CF2048G Kevin and Matrices

容易发现 \(\mathrm{LHS}\ge\mathrm{RHS}\)，那么只需要计数 \(\mathrm{LHS}=\mathrm{RHS}\) 的方案数 .

令 \(f(x,y)\) 表示 \(\mathrm{LHS}\ge x,\,\mathrm{RHS}\le y\) 的方案数，只需要计算 \(O(v)\) 个 \(f\) 即可拼出答案 .

关于 \(f(x,y)\)，可以对 \(x\) 用二项式反演、对 \(y\) 用单步容斥：钦定 \(i\) 行不存在 \(\ge x\) 的 max，

\[f(x,y)=\sum_{i=0}^n(-1)^i\dbinom ni(v^{n-i}(x-1)^i-(v-y)^{n-i}\max\{x-y-1,0\}^i)^m \]

那么可以在 \(\tilde \Theta(nv)\) 的时间复杂度内计算出答案 .

[JOI 2023 Final] 迷宫

常数理论神题，写以 \(n\) 为块长分块优化建图就爆炸了 .

相当于每次走四连通方向的一步，走的时候可以花费 1 的代价让后面的 \(n-1\) 步改成八连通步且可以经过障碍 . 使用 0-1 BFS 即可 \(\Theta(rc)\) 解决 .

TopCoder 14563 - DerangementsStrikeBack

考虑使用递推计算错排的技术，现在计算 \(D_i\)：

  • 若 \(p_i=j<i\)：若 \(p_j=i\) 那么删去 \(j,i\) 即可转为长为 \(n+i-2\) 的问题；否则找到 \(p_k=i\)，将 \(p_k\) 改为 \(j\)，然后删去 \(i\) 即可转为长为 \(n+i-1\) 的问题 .
  • 若 \(p_i=j>i\)：找到 \(p_k=i\)，将 \(p_k\) 改为 \(j\)，然后删去 \(i\) 即可转为长为 \(n+i-1\) 的问题 .

从而 \(D_i=(i-1)(D_{i-2}+D_{i-1})+n\cdot D_{i-1}=(n+i-1)D_{i-1}+(i-1)D_{i-2}\)，其中 \(D_0=1,\,D_1=n\cdot n!\) . 那么可以在 \(\Theta(m)\) 时间内解决原问题 .

[JOI Open 2022] 跷跷板

注意到，对于一个箱子方位 \([l,r]\)，如果对于每种区间长度，都存在一个区间的重心位于 \([l,r]\) 内，那么这个箱子方位就是合法的 .

进而容易发现对于每种区间长度只有离初始重心最近的区间才有用，此处两个方向分别有一个关键区间 . 这样就变成这样一个问题：给 \(n\) 个二元组 \((u,v)\)，每个二元组中选一个元素，最小化极差 . 排序之后单调指针即可随意完成 .

[GDKOI2024 提高组] 染色

考虑用 \(\mathbb F_2\) 上模 \((x^{2^n-1}-1)(y^{2^n-1}-1)\) 意义下的二元多项式描述一个棋盘 . 对于两个棋盘 \(P,Q\)，其中 \(Q\) 描述操作：若 \(Q_{i,j}=1\)，则对 \(P\) 的 \((i,j)\) 位置进行一次操作 . 那么容易发现操作之后的棋盘就是 \(P+K(x,y)\cdot Q\)，其中 \(K(x,y)=x+y+x^{-1}+y^{-1}+1\) .

那么对于给定的棋盘 \(A\)，就是要求 \(A\cdot K(x,y)^{-1}=A\cdot K(x,y)^{2^{n-1}-1}\) . 又由于 \(K(x,y)^2=K(x^2,y^2)\)，所以可以在 \(\Theta(4^n)\) 时间内简单算出答案 .

[JOISC 2020] 収穫

首先看成苹果逆时针转，遇到一个员工就跳 \(C\) 步 . 那么可以处理出苹果遇到每个员工时下一步会跳转到的员工编号，这样可以形成一张基环内向树森林 .

现在考虑查询，要求员工 \(x\) 在 \(T\) 时刻的收获 . 对每个连通块分别考虑 . 首先对于树上的点可以随意二维数点解决；对于环上的点，令 \(p_i\) 是离 \(i\) 最近的环上的点、\(w_i\) 是碰到 \(p_i\) 的时间、\(l\) 是环长、\(s_i\) 是环上 \(i\) 位置的后缀和，答案即为：

\[\begin{aligned}\mathrm{ans}&=\sum_i[T\ge w_i+\dist(p_i,x)]\left(\left\lfloor\frac{T-w_i-\dist(p_i,x)}l\right\rfloor+1\right)\\&=\sum_i[T+s_x\ge w_i+s_{p_i}+[p_i>x]\cdot l]\left(\left\lfloor\frac{T+s_x-w_i-s_{p_i}}l\right\rfloor-[p_i>x]+1\right)\\&=\sum_i[v\ge q_i+[p_i>x]\cdot l]\left(\left\lfloor\frac{v-q_i}l\right\rfloor-[p_i>x]+1\right)&(v=T+s_x,\,q_i=w_i+s_{p_i})\\&=\sum_i[v\ge q_i]\left(\left\lfloor\frac{v-q_i}l\right\rfloor-[p_i>x]+1\right)\\&=\sum_i[v\ge q_i]\left(\left\lfloor\frac vl\right\rfloor-\left\lfloor\frac{q_i}l\right\rfloor-[v\bmod l<q_i\bmod l]-[p_i>x]+1\right)\end{aligned} \]

第四个等号：可以发现将 \(v\) 的限制放松 \(l\) 不会影响括号内部的值 .

第五个等号：拆整除 \(\lfloor\frac{a-b}c\rfloor=\lfloor\frac ac\rfloor-\lfloor\frac bc\rfloor-[a\bmod c<b\bmod c]\) .

那么就可以二维数点了 .

[NOIP2024] 树上查询

首先区间 LCA 的深度就是序列上相邻位置 LCA 的深度 min，那么就变成算区间内长度 \(=k\) 的子区间 min 的 max .

对于每个数 \(v\) 计算它作为 min 的区间 \([x,y]\)，那么 \(v\) 能贡献到 \([l,r]\) 当且仅当下列两个条件之一成立：

  • \(y_i\ge r\) 且 \(x_i\le r-k+1\) .
  • \(l+k-1\le y_i\ge r\) 且 \(y_i-x_i+1\ge k\) .

分别是二维偏序，扫描线即可 .

[JOI Open 2018] 木琴

考虑问出每个 \((i,i+1)\) 的答案 \(b_i\) 和 \((i-1,i+1)\) 的答案 \(c_i\) . 令 \(d_i=a_{i+1}-a_i\)，首先显然有 \(|d_i|=b_i\) . 通过讨论可以得到当且仅当 \(b_{i-1}+b_i=c_i\) 时 \(d_{i-1},d_i\) 同号，那么可以确定每个 \(d_i\) 的符号，进而通过枚举 \(d_1\) 的符号可以确定每个 \(d_i\)，从而可以简单得到每个 \(a_i-a_1\) . 接下来还原 \(a\) 就是简单的了 .

总共询问 \(2n-3\) 次 .

[JOISC 2022] 一流团子师傅

首先对于一个填了若干团子的串可以判断一个新的团子是否能里面：取不在串上也不是新的团子的团子查询一下，判断答案是否 \(\ge n-1\) . 那么可以扫 \(m\) 遍，每次尝试将某个团子加入到某个串上面，这样的询问次数是 \(nm^2\) 级别的 .

对于一个团子 \(x\) 可以通过二分快速定位到一个可能的串：对于集合 \(S\)，将 \(x\) 和 \(S\) 内的元素去掉询问一次，如果答案 \(\ge n-|S|\) 那么 \(S\) 里有答案 . 这样就可以到不超过 \(nm\lceil\log_2m\rceil\) 次询问了，可以通过 .

[集训队互测 2024] 基础 ABC 练习题

这不是我们 ABC Ultimatum 的梗吗，转载记得注明出处（

令 \(f_{\sf BA}\) 是前缀 B 的数量减 A 的数量的最大值，同理定义 \(f_{\sf CB},f_{\sf AC}\) .

断言：对于每个三元组 \((x,y,z)\) 满足 \(x+y+z=n\) 且 \(x\ge f_{\sf BA},\,y\ge f_{\sf CB},\,z\ge f_{\sf CA}\)，都存在一种划分使得划分成恰好 \(x\) 个 BCA、\(y\) 个 CAB、\(z\) 个 ABC . 证明可见官方题解 .

那么枚举两个 \(f\)，可以计算出另外一个 \(f\) 是什么 . 接下来大力 DP 记 A, B, C 的个数即可 \(\Theta(n^5)\) .

QOJ #8233. Operator Precedence

\(n\) 是奇数：\(1,1,(-2,-1,2,-1,2,1,-2,1)^{\infty}\) 截断到 \(2n\) 位 .
\(n\) 是偶数：\(1,(1,-2,1,-2,-1,2,-1,2)^{\infty}\) 截断到 \(2n\) 位 .

[APIO2025] 转杆

排序之后依次将 \(i\) 和 \(i+\lfloor\frac n2\rfloor\) 转成垂直的，正确性易证 .

[APIO2025] Hack!

千言万语汇成 0 句话

[JOISC 2022] 蚂蚁与方糖

首先有显然的二分图匹配模型，使用 Hall 定理可得答案即为 \(|A|-\max\limits_S\{|S|-|N(S)|\}\) .

将 \(S\) 按 \(N\) 的方位划分成若干区间，那么相当于找区间簇 \([l,r]\) 最大化 \(\displaystyle\sum(\operatorname{sumA}(l,r)-\operatorname{sumB}(l-L,r+L))\)，区间离得太近以至于 \([l-L,r+L]\) 有交则一定不优 . 把左右端点附近的贡献分别拆开就可以写成简单 DP 的形式了 . 后面大概就是线段树维护两个界点选 / 不选的 DP 信息，可以轻松合并 . 修改的时候仔细考虑一下就可以转成打标记的形式 . 时间复杂度 \(O(Q\log Q)\) .

[JOISC 2022] 复制粘贴 3

\(dp_{l,r}\) 表示区间 \([l,r]\) 的答案，刷表进行转移：枚举 \(l,r,k\)，找到最大的 \(p\) 使得 \([l,r]\) 在 \([p,r]\) 中不重复地出现了至少 \(k\) 次，然后转移 \([p,r]\gets[l,r]\) .

显然 \(k\) 是 \(\frac{n}{r-l+1}\) 级别的，所以总枚举量是调和级数 . 关于如何找到 \(p\)，可以考虑处理每个区间 \([l,r]\) 的上一次出现位置（可以通过处理 LCP 等递推得到），接下来枚举 \(k\) 的时候让 \(p\) 每次往前跳一个 \([l,r]\) 就可以了 .

时间复杂度 \(\Theta(n^2\log n)\) .

[JOI Open 2018] 冒泡排序 2

显然趟数相当于每个点走到它的排名的步数最大值，依次加入每个数可以得到就是 \(\max\limits_i\left\{i-\sum_{j=1}^i[a_j\le a_i]\right\}\) .

决策点右边肯定没有比它小的数，所以可以把 \(\sum_{j=1}^i[a_j\le a_i]\) 弱化到 \(\sum_{j=1}^n[a_j\le a_i]\)，这样就随便维护了 .

时间复杂度 \(O(n\log n)\) .

SPOJ EXLAGFIB - Extremely Lagged Fibonacci

填一下一年前 NFLS 模拟赛的坑

欲求 \([x^n]\dfrac{x^{k-1}}{1-bx^j-cx^k}=[x^{n-k+1}]\dfrac1{1-bx^j-cx^k}\)，考虑到：

\[[x^n]\dfrac1{1-bx^j-cx^k}=\sum_{i\ge0}[x^n](bx^j+cx^k)^i=\sum_{pj+qk=n}\dbinom{p+q}qb^pc^q \]

那么只需要计算 \(\Theta(\frac nk)\) 个组合数之和（这里组合数可以使用 Lucas + CRT 求解）.

[JOI Open 2022] 放学路

首先由于子任务 3 考虑广义串并联图方法，缩合随时不缩 \(1,n\) 这两个点，每次叠合重边的时候如果两条边边权不一样那么标记为 \(-1\) .

大概感受一下可以猜想如果最后只剩下一条 \(1\to n\) 且边权不为 \(-1\) 那么答案就是 0 . 然而现实是这个猜想只在点双上成立（虽然提交可以直接通过）：

证明

首先把图按最短路方向定向 . 接下来如果一个点的入度小于出度则称其为红点否则为蓝点 .

那么考虑 \(1\rightsquigarrow n\) 中经过边数最多的一条路径，它的开头入度一定为 1、结尾出度一定为 1，那么路径上一定存在一条边 \(u\to v\) 使得 \(u\) 是红点、\(v\) 是蓝点 . 那么一定存在 \(u\to x,\,y\to v\) 两条边 .

考察路径 \(1\rightsquigarrow y\to v\to u\to x\rightsquigarrow n\)，如果它不是简单路径那意味着 \(1\rightsquigarrow y,\,x\rightsquigarrow n\) 有交点 \(z\)，此时 \(1\rightsquigarrow x\rightsquigarrow z\rightsquigarrow y\rightsquigarrow n\) 比原来的路径更长，矛盾 . 所以 \(1\rightsquigarrow y\to v\to u\to x\rightsquigarrow n\) 一定是简单路径，且它的长度比最短路长 .

其实问题也不大，对于任意图来说对 \(1,n\) 之间的点双分别做就可以了 . 实现上可以连 \((1,n,\dist(1,n))\) 然后考虑 \(1,n\) 所在的点双 . 时间复杂度 \(O(m\log m)\) .

[Ynoi Easy Round 2018] 星野爱

首先改成给一个序列 \(a\)，区间 \(w_{a_i}\gets w_{a_i}+v\) 查区间 \(w_{a_i}\) 之和 .

对 \(a\) 分块，将修改和询问之间的贡献分为三种：

  • 散块对散块：暴力 .
  • 散块对整块：处理一下每个点在每个块的出现次数，这样就可以算出来修改对询问的贡献了 .
  • 整块对散块 / 整块：类似上一个处理每个点在每个块的出现次数做就行了 .

需要通过一些离线技巧做到线性空间，如果一个点的入度为零那么它对应的区间可能会出现 \(l>r\) 的情况，需要特判 .

令 \(n,m,q\) 同阶，时间复杂度 \(O(n\sqrt n)\)，空间复杂度 \(\Theta(n)\) .

[NAC 2025] Most Scenic Cycle

一眼看穿图是广义串并联图，直接做即可 . 实现上，可以在 twist 的时候统计答案 .

[JOISC 2023] Security Guard

省流：对于树来说每次全局减最小值把 0 的位置缩起来递归进入，可得答案即为以 \((u,v,a_u+a_v)\) 为边的图的 MST 加 \(\max a_i-\sum a_i\) . 倒着看最后是以最小值为根的菊花每次选一个根上的边删了换成一个原图的边，可并堆（或者启发式合并）动态维护一下连通块即可 . 时间复杂度 1~2 log .

[JOI 2025 Final] 只不过是长的领带 2

考虑如果知道哪些位置回应的话，只需要动态维护一个集合 \(S\)，依次加入每个数替换掉不大于它的最大的数，如果没有这样的数就把它加进 \(S\) 里 . 最后 \(S\) 的大小即为答案 .

由于 \(S\) 内的元素明显是不重复的，所以只有 \(2^V\) 种状态 . 那么有显然的 \(\Theta(n2^V)\) DP：令 \(dp_{i,S}\) 表示考虑 \(1\dots i\) 且选中 \(i\)、目前集合为 \(S\) 是否合法 . 由于实际上对于一个 \(S\) 只关心满足 \(dp_{i,S}=1\) 的最大的 \(i\)，那么可以改写为 \(dp_S\) 表示集合 \(S\) 能表示的最大的 \(i\) .

转移得到的新的集合可以简单处理出来 . 这里转移有自环需要先处理掉，表现上就是找出最大的 \(a_i,a_{i+1}\neq S\) 的位置 \(i\) 更新答案 . 可以处理一下每个位置 \(i\) 后面的第一个 \(a_i,v\) 出现的位置，那么就可以在 \(\Theta(nV)\) 预处理后以 \(\Theta(V^2)\) 时间计算自环的转移了 .

总时间复杂度 \(\Theta(nV+V^22^V)\) .

[Ynoi Easy Round 2024] TEST_130

\([L_u,R_u]\) 是 \(u\) 子树内的结点在 DFS 序上对应的区间，\(\dep(u),\,\mxd(u)\) 是深度（根的深度为 1）和子树的高度 .

那么一次询问 \((u,d)\) 相当于对于所有 \(v\in[L_u,R_u]\)，求和：

\[f(v)=1+\begin{cases}\mxd(v)&\mxd(v)+\dep(v)<d+\dep(u)\\d+\dep(u)-\dep(v)&\mxd(v)+\dep(v)\ge d+\dep(u)\\-(d+\dep(u)-\dep(v))&\dep(v)>d+\dep(u)\end{cases} \]

每个限制都是二维偏序，可以直接扫描线 + 树状数组完成 . 需要大力压缩一下二维偏序的个数才能通过 .

时间复杂度 \(\Theta((n+m)\log n)\)，Submission .

[JOISC 2022] 错误拼写

直接对字符串 \(S\) 考虑，从后往前 DP：\(dp_{i,j}\) 表示 \(s_i=j\) 的方案数 . 对于一个限制 \((u,v)\)（\(u\le v\)）来说，它对从 \((i',j')\) 出发的转移的影响：

  • 若 \(T_u\le T_v\)，则 \(i'\in(u,v]\) 转移到 \(i'\) 之前的位置 \((i,j)\) 时，必须有 \(j>j'\) .
  • 若 \(T_u\ge T_v\)，则 \(i'\in(u,v]\) 转移到 \(i'\) 之前的位置 \((i,j)\) 时，必须有 \(j<j'\) .

那么对于固定的 \(i'\) 来说它能转移到的区间是有一定单调性的，再维护一个当前处理过的 DP 数组对 \(dp_{-,i}\) 的贡献，转移的时候用链表维护活跃的 \(i'\) 就可以了 . 时间复杂度 \(\Theta(n|\Sigma|)\) .

[JOISC 2020] 治療計画

通过仔细地考虑可以得到：若 \(R_i-L_j+1\ge|T_i-T_j|\) 则连 \(i\to j\)，从左边界走到右边界的最短路即为答案 .

那么给 \(T\) 排序将限制拆成两个二维偏序，线段树维护每个点能到达的点即可 . 由于点权最短路 Dijkstra 每个点只会被松弛一次所以复杂度可以均摊到 \(O(m\log m)\) .

[NOIP2024] 树的遍历

对于一棵树来说，能当根的位置一定是原树的一条叶子到叶子的链 . 如果确定了这条链 \(C\)，那么新树的方案数为：

\[\prod_u(\deg u-1)!\prod_{u\in C}(\deg u-1)^{-1} \]

接下来简单树形 DP 即可，时间复杂度 \(\Theta(n)\) .

[JOI 2018 Final] 团子制作

首先有显然的二分图最大独立集模型，注意到每个左部点的出点是右部点一个区间，所以直接贪心即可 .

[ICPC 2024 Yokohama R] Beyond the Former Explorer

Hint 1：如果知道了一行的方向，可以判断 G 具体在这一行的哪边 .

Hint 2：同时对行 / 列进行二分 .

[PA 2025] 瞬间传送

枚举答案 \(r\)，注意到如果 \(\dist(i,j)>r\) 而加入边 \((u,v)\) 后可以解决问题（不妨令 \(\dist(i,u)\le\dist(i,v)\)），那么 \(i\to j\) 的最短路一定是 \(i\to u\to v\to j\) .

那么枚举 \(r=n\dots 1\) 的过程中随时维护合法的 \((u,v)\)，对于每对距离大于 \(r\) 的 \((i,j)\) 在 \(i\) 上维护 \(\max\limits_v\dist(v,j)\) . 精细实现可以保证每轮只检查转为不合法的 \((u,v)\) ，则可以均摊到 \(O(n^3)\) 时间 .

[JOI Open 2024] 图书馆 3

原问题显然等价于交互库有一个排列 \(p\) 每次可以问一个排列 \(q\) 返回 \(p\circ q\) 的置换环个数 .

考虑增量维护，假如 \(p\circ q\) 的 \(1\dots i\) 位是单位排列，可以通过二分来确定第 \(i+1\) 位和 \(1\dots i\) 中哪个元素在同一置换环上或报告不存在，这样就 \(\Theta(n\log n)\) 次了 .

QOJ #3082. Ascending Matrix

先不考虑 \(a_{r,c}=v\) 的限制 . 考察数值的分界线，可以得到 \(k-1\) 条 \((n,0)\to(0,m)\) 的互不击穿的路径 . 对于第 \(i\) 条路径，做变换 \((x,y)\to(x+i,y+i)\)，那么即转为 \(k-1\) 条不交路径 .

显然路径簇和矩阵双射，那么只需要考虑不交路径簇的个数，使用 LGV 引理即可简单解决 . 对于 \(a_{r,c}=v\) 的限制，相当于点 \(p=(r+v-2,c+v-2)\) 上面只有 \(v-1\) 条路径，且 \(p\) 不被任何路径经过 . 加入形式变元 \(x\) 计量 \(p\) 上方的路径个数，这只需要将 \(p\) 右上方的位置的权值乘 \(x\)，此后同样使用 LGV 引理即可 .

时间复杂度 \(\Theta(k^4)\) . 如果使用更快的计算 \(\det(A+Bx)\) 的算法可以优化到 \(\Theta(k^3)\) .

CF1874F Jellyfish and OEIS

结果还是到这一步了……？Solution .

CF773F Test Data Generation

显然限制相当于 \(n\) 是奇数、\(a_n\) 是偶数、\(a_n/g\) 是奇数 . 枚举 \(g\) 有多少个因子 2 即可得到答案的表达式：

\[\sum_{i\ge1}f\left(\left\lfloor\dfrac{\lfloor\frac A{2^i}\rfloor-1}2\right\rfloor,\left\lfloor\dfrac{N-1}2\right\rfloor\right)\text{ where }f(x,y)=\sum_{i=0}^x\sum_{j=0}^y\dbinom{2i}{2j} \]

那么只需要求 \(\Theta(\log A)\) 个 \(f(x,y)\) 的值 . 令 \(a_j=\sum_{i=0}^x\binom{2i}j\)，则

\[\begin{aligned}a_j&=\sum_{i=0}^x\dbinom{2i+1}{j+1}-\sum_{i=0}^x\dbinom{2i}{j+1}\\&=\sum_{i=0}^{2x+1}\dbinom i{j+1}-2\cdot a_{j+1}\\&=\dbinom{2x+2}{j+2}-2\cdot a_{j+1}\end{aligned} \]

也即 \(a_{j+1}=\frac12\left(\binom{2x+2}{j+2}-a_j\right)\) .

由于 \(N\) 比较小可以考虑暴力进行递推 . 令 \(p=(2p_1+1)2^{p_0}\)，首先考虑对 \(2p_1+1\) 取模求出每个 \(a\)，这里可以使用类似 Nephren Runs a Cinema 的方法处理组合数 . 接下来使用反向的递推式 \(a_j=\binom{2x+2}{j+2}-2\cdot a_{j+1}\) 做 \(p_0\) 步即可求出每个真实的 \(a\)（由于此处递推式对 \(a\) 每次乘 2，做 \(p_0\) 次即可消除对应错误的贡献）.

时间复杂度 \(O(N\log p\log A)\) .

CF1553I Stairs

首先能求出每个阶梯的长度 \(b_{1\dots m}\)，接下来其实该二项式反演了：令 \(f_{i,j}\) 表示 \(b_{1\dots i}\) 组成至多 \(i\) 段的方案数，那么答案即为

\[\sum_{i=1}^m(-1)^{m-i}\cdot i!\cdot f_{m,i} \]

所以此处只需求 \(f_{m,\cdots}\) . 对行建立生成函数 \(F_m(x)\)，令 \(S_m(x)=\sum_{i=0}^mF_m(x)\)，则有：

\[F_0(x)=1\qquad F_i(x)=\begin{cases}x\cdot F_{i-1}(x)+2x\cdot S_{i-2}(x)&b_i=1\\2x\cdot S_{i-1}(x)&b_i>1\end{cases} \]

写成矩阵分治乘就可以了，时间复杂度 \(O(\mathsf M(n)\log n)\) .

洛谷 P8859 冒泡排序

首先 \(type=1\) 相当于前缀最大值个数为 \(n-k\)，随意做即可（或者说第一类 Stirling 数）.

对于 \(type=2\) 来说考虑固定 \(n\) 在最后一位，\(dp_{i,j}\) 表示长度为 \(i\)、次数为 \(j\) 的方案数，则

\[dp_{i,\max(p+1,q)}=\sum_{j=0}^{i-1}\dbinom{i-1}j\cdot dp_{j,p}\cdot dp_{i-j-1,q} \]

max 卷积可以前缀和优化，\(\Theta(n^3)\) 解决 .

CF1707D Partial Virtual Trees

教你怎么用二项式反演（详细揭秘）

\(G(k)\) 是答案，\(F(k)\) 是 \(\subsetneq\) 改成 \(\subseteq\) 的答案 . 对于 \(F(i)\)，枚举有多少位满足 \(\subsetneq\) 可得：

\[F(i)=\sum_{j=1}^i\dbinom ijG(j) \]

后面比较简单就不写了。。

[JOI 2022 Final] 沙堡 2

一个基本的思路是考虑矩形内每个点连它旁边能走的最大的点，这样一个矩形合法当且仅当只有 1 个点没有出度 .

接下来大概就都是若干种情况分讨了 . 一种比较方便的做法是对于 \((i,j)\) 设四周最小的比它大的数为 \(t\)，否则为极大值 \(t=X\) . 若存在比它小的数则权值为 \(t-a_{i,j}\)，否则为 \(t\) . 则一个矩形合法当且仅当它的权值和为 \(X\) .

小的一维枚举区间、大的一维类似 2-SUM 做即可 \(\Theta(nm\min\{n,m\})\) .

[WC/CTS2024] 水镜

问题在于这个递增的限制基本上只和相邻的位置有关。。

[PA 2024] Modernizacja Bajtocji

如果没有 - 就是并查集判环就行了 . 如果有 - 的话可以聪明一下给 - 的位置新开一个点，这里只有连通块大小 =2 的时候 - 会提供额外信息 .

[POI 2015] LOG

无语。请看 Re:2025.6.25 闲话。

[JOI Open 2018] 山体滑坡

(APIO2019 桥梁)'s trick

我写的根号重构：每 \(\Theta(\sqrt m)\) 次修改原图，接下来每次询问都相当于加 \(O(\sqrt m)\) 条边后问连通块数量 . 此处可以只把关键点拉出来做并查集，这样就不用可撤销了 .

CF1874D Jellyfish and Miku

一阶线性递推都不会？首先 \(a_i\) 固定则答案为 \(\displaystyle\sum_{i=1}^na_i\sum_{j=1}^{i-1}\dfrac1{a_j}\)，显然 \(a_i\) 单调不降否则不优，所以朴素 DP 的转移其实是调和级数时间复杂度的 . 时间复杂度 \(O(nm\log m)\) .

CF1796F Strange Triples

CF2039F Shohag Loves Counting

我怎么开局推的 DP 式子就是转置之后的大众做法。。后续纯属随意说明不建议我之外的人看（

转移方程如下：

换元可以改写为：

\[f_{i,j}=\sum_{k,l}f_{k,l}\left[l\perp\frac jk\right]=\sum_{kd\mid j}\mu(d)\sum_lf_{k,dl} \]

这里仔细地实现就是 \(\Theta(d_3(n))=\Theta(n\log^2n)\) 了 . 恭喜你 skip 掉 Easy Version 直接破解 Hard Version .

洛谷 P5605 小 A 与两位神仙

死去的记忆突然开始攻击我。。答案为 Yes 当且仅当 \(\ord_m(y)\mid\ord_m(x)\) .

CF1774G Segment Covering

怎么卡数据结构部分了。有点爆。数学题单你就真只会数学部分是吧。

首先注意到如果区间 \(I_1\subseteq I_2\) 那么可以把 \(I_2\) 去掉（因为贡献会抵消），此后区间只包含不相交 . 另外如果区间 \(I_3\subseteq I_1\cup I_2\) 那么相当于 \(I_1,I_2\) 不能同时选 . 从左到右考虑每个区间就相当于这样一个问题：从最左边的区间开始，如果当前的区间是 \(I=[l,r]\)、上一个区间是 \(I_0=[l_0,r_0]\)，接下来选的区间 \(I'=[l',r']\) 必须满足 \(l'\in(r,r_0]\)（否则会构成 \(I\subseteq I_0\cup I'\)）且左端点最小 . 可以发现选中的区间簇其实是唯一的 .

然而过程其实相当于从最左边的两个区间 \(I_1,I_2\) 开始，每次分别转移到最近的不交的区间，问走到右端点的步数，如果能走到的话需要最终的区间不相等（否则说明中间有空隙） . 可以倍增处理，时间复杂度 \(\Theta((m+q)\log m)\) .

[JOI 2016 Final] 断层

真就直接维护啊 . 首先时间倒流之后变成求初始 \(x\) 轴的点都到了哪里 . 接下来把坐标系转 45 度每次操作只和 \(x,y\) 中的一个相关，可以随意维护 .

时间复杂度 \(O((n+q)\log n)\) .

[Ynoi2002] Goedel Machine

对于素因子根号分治：

  • 对于小于根号的素数：直接暴力枚举每个素数幂计算对每个询问的贡献 .
  • 对于大于根号的素数：由于每个素因子最多一次，所以可以随意 \(O(1)\) 计算加入 / 删除一个数的贡献，莫队即可 .

令 \(n,m,A\) 同阶，时间复杂度 \(O(n\sqrt n)\) .

[JOIST 2023] 曲奇 / Cookies

令 \(c_i\) 是大小 \(\ge i\) 的盒子数量（这意味着 \(c\) 肯定是单调不增的）. 首先有显然的网络流模型，调用 Gale-Ryser 定理可得合法当且仅当：

  1. \(\sum c_i=\sum a_i\) .
  2. 对于每个 \(k\)，\(\sum_{i\le k}c_i\ge\sum_{i\le k}a_i\) .
  3. \(c_k\neq c_{k+1}\implies k\in B\)

其中 \(a\) 按降序排序 .

如果知道 \(c\) 数组那么贪心匹配即可求出答案 . 此处朴素背包是 \(O(n^3)\) 的，然而有一维上界是调和级数的可以改成 \(O(n^2\log n)\)，进一步使用 bitset 优化可以到达 \(O(n^2\log n/w)=O(n^2)\) .

Gym103415K. Magus Night

流汗，本题最难的部分在于将 \(\lcm\ge p\) 转为 \(\lcm<p\) 后进行计算，后面非常简单就不写了 .

[AGC038E] Gachapon

唉，百鸽笼's trick……有点怀念啊（

令 \(p_i=\dfrac{a_i}S\) . 枚举最后一步取的是哪个数，可以得到答案的表达式：

\[\begin{aligned}&F_i(x)=\mathrm e^{p_ix}-\sum_{k=0}^{b_i-1}p_i^k\dfrac{x^k}{k!}\\&G_i(x)=p_i^{b_i}\dfrac{x^{b_i-1}}{(b_i-1)!}\\&H(x)=\sum_{i=1}^nG_i(x)\prod_{j\neq i}F_j(x)\\&\mathrm{ans}=(\mathcal LH)'(1)\end{aligned} \]

可以考虑大力维护出 \(H\) 的每个 \(\mathrm e^{x/S},x\) 的系数，接下来使用 \((\mathcal Lx^a\mathrm e^{bx})'(1)=\dfrac{a!(a+b)}{(1-b)^{a+2}}\) 即可计算答案 .

假设 \(n,\sum a,\sum b\) 同阶则时间复杂度为 \(O(n^3)\) .

[Ynoi2024] 弥留之国的爱丽丝

首先需要明确一下给的图不一定是 DAG . 某种意义上可能是另一个方向的 Range Reachability Query？

时间轴按 \(B\) 分块，每次取出关键点用黑色的非关键边缩点并处理出 DAG 可达性，每次询问的时候 BFS 判断（这里也用 bitset 优化）.

总时间复杂度 \(O(\frac qB(n+m+\frac{(n+m)B}w)+q\frac{B^2}w)=O(\frac{q(n+m+B^2)}w+\frac{q(n+m)}B)\) . 取 \(B=((n+m)w)^{1/3}\) 即可 \(O(\frac{q(n+m)}w+\frac{(q(n+m))^{2/3}}w)\)（由于这里瓶颈实际上在 DAG 可达性方面所以块长随意取也不太影响复杂度）.

[AGC034F] RNG and XOR

首先有概率 DP：

\[\begin{aligned}&f_0=0\\&f_S=1+\sum_if_{S\oplus i}p_i\end{aligned} \]

施 FWT（由于此处关于 \(\varnothing\) 位置的修正系数并不那么显然故设为 \(c\)）：

\[\FWT(f)=\FWT(\bm 1)+\FWT(f)\FWT(p)+c \]

考察 \(\varnothing\) 次项可得 \(c=-2^n\)，那么对于不为 \(\varnothing\) 的位置有：

\[\FWT(f)=-\dfrac{2^n}{1-\FWT(p)} \]

对于 \(\varnothing\) 位置可以通过别的位置求出 .

从而只需要做一些 FWT 即可获得答案，时间复杂度 \(\Theta(n2^n)\) .

[Ynoi2006] rldcot

一个支配对的题目 . 根据虚树的结论可以知道只有编号相邻的 LCA 是关键的，那么可以 dsu on tree 维护每个支配点对，这一部分是 \(O(n\log^2n)\) 得到 \(O(n\log n)\) 个支配对 . 接下来是 2-side 矩形数颜色，对每个点对考虑对哪些区间有贡献，相当于对每种颜色做矩形并之后统计一个询问被多少个矩形覆盖，这是简单的 .

总时间复杂度 \(O(n\log^2n+q\log n)\) .

CF623E Transforming Sequence

省流：

\[\mathrm{ans}=\left[\dfrac{x^k}{k!}\right]\mathrm e^x\prod_{i=0}^{n-1}(\mathrm e^{2^ix}-1)=\sum_{i=0}^{2^n-1}(-1)^{\popcount(i)}(i+1)^k \]

经验主义地谈应该是不太能做得倍增还好的……时间复杂度 \(\Theta(\mathsf M(k)\log\min(n,k))\)，需要使用 MTT .

[AGC065D] Not Intersect

枚举有多少条弦连接相邻的位置，接下来计数多边形剖分 . 断 \(1-n\) 改成边作为区间只包含不相交（区间钦定选 \([1,n]\)），可以用类似括号匹配的栈来判定，进一步可以改写为一组和为 1 的数前缀和随时为正则合法 . 根据 Raney 引理所有循环移位恰有一个合法，所以只需要计数随意的序列然后除即可 . 答案的表达式可以贺题解区得到 .

CF765F Souvenirs

另一类支配对问题 . 固定左端点那么每取到一个决策点值域除以二，所以对于固定左端点来说支配对个数是 \(O(\log V)\) 级别的 . 询问的时候二维数点就可以了，时间复杂度 \(O(n\log^2V+q\log n)\) .

[AGC021F] Trinity

一、考虑只保留被 \(A,B,C\) 计算的位置转为数每个黑格上下左至少有一侧全白的表格数量 .

二、接下来可以从后往前 DP：\(f_{i,j}\) 表示考虑了 \(i\) 列、目前有 \(j\) 行没放黑格的方案数 . 则有：

\[f_{m,n}=f_{m+1,n}+\dbinom{n+1}2f_{m-1,n}+\sum_{i=0}^{n-1}\dbinom{n+2}if_{m-1,i} \]

三、对行建立 EGF，通过仔细地简化可以得到

\[F_m(x)=\mathrm e^xF_{m-1}(x)+(2\mathrm e^x-x-2)F_{m-1}'(x)+(\mathrm e^x-x-1)F_{m-1}''(x) \]

迭代列通常是难以处理的，不过此处可以大力维护 \(x,\mathrm e^x\) 的系数，这样就是 \(O(m^3)\) 的了 .

[AGC020F] Arcs on a Circle

在最长的弦的一侧破环为链，接下来暴力枚举每个弦端点小数部分的大小关系 . 每段打 \(n\) 个断点离散化得到 \(nc\) 个关键位置，接下来可以 DP：\(f_{i,j,S}\) 表示左端点 \(\le i\) 的线段放完、覆盖到的最大坐标为 \(j\)、选中集合 \(S\) 的弦的方案数 .

时间复杂度 \(O(n!2^nn^2c^2)\) .

[SDOI2014] 向量集

显然维护个凸包就完了，希望使用对数据结构的爱的技术线段树维护，不过在线有点麻烦 . 由于只有末尾插入，这里可以类似二进制分组地均摊，加入位置 \(p\) 时只有当前结点 \([l,r]\) 满足 \(p=r\) 才 pushup，这样就是对的了 .

时间复杂度 \(O((n+q)\log^2n)\) .

[AHOI2022] 山河重整

请看 EI 的 [AHOI2022] 山河重整 解析 .

\(a_{k+1}\) 表示和为 \(k\) 且能表达 \(1\dots k\) 的集合数量，则有

\[\sum_{k\ge0}a_k\prod_{i\ge k}(1+x^i)=x\prod_{i\ge1}(1+x^i) \]

求出 \(a\) 之后答案就是 \(2^n-\sum_{k=1}^n2^{n-k}a_k\) .

考虑一个互异分拆数的拆法：

\[\prod_{i\ge k}(1+x^i)=\sum_{j\ge 0}x^{j(j-1)/2+jk}\prod_{i=1}^j\dfrac1{1-x^i} \]

则：

\[\begin{aligned}x\prod_{i\ge1}(1+x^i)&=\sum_{k\ge0}a_k\prod_{i\ge k}(1+x^i)\\&=\sum_{k\ge0}a_k\sum_{j\ge 0}x^{j(j-1)/2+jk}\prod_{i=1}^j\dfrac1{1-x^i}\\&=\sum_{j\ge0}x^{j(j+1)/2}\prod_{i=1}^j\dfrac1{1-x^j}\sum_{k\ge0}a_kx^{(j+1)k}\\&=\sum_{j\ge0}x^{j(j+1)/2}A(x^{j+1})\prod_{i=1}^j\dfrac1{1-x^j}\\A(x)&=x\prod_{i\ge1}(1+x^i)-\sum_{j\ge1}x^{j(j+1)/2}A(x^{j+1})\prod_{i=1}^j\dfrac1{1-x^j}\end{aligned} \]

其实类似于一个半在线的过程，首先倍增转为离线，接下来 \(j\) 从大到小扫随时维护即可 . 时间复杂度 \(\Theta(n\sqrt n)\) .

『JROI-4』少女幻葬

看这个做法给我一种阅读 zak 科技的感觉……

不妨令 \(k=1\) . 设 \(f_{i,j,k}\) 表示考虑前 \(i\) 个数、\(a_i=k\)、\(\gcd(a_i,a_{i-1})=j\) 的方案数，设 \(g_{i,j,k}\) 表示考虑前 \(i\) 个数、\(a_i=k\)、\(\gcd(a_i,a_{i+1})=j\) 的方案数 .

此处后两维的状态数是 \(O(m\log m)\) 级别的，所以总状态数是 \(O(nm\log m)\) 级别的 .

\(\bm{g\to f}\)

\[f_{i,j,k}=\sum_{v\mid j}g_{i-1,j,v}[\gcd(v,k)=j] \]

枚举 \(j\) 并提取 \(j\) 的倍数即可转为：

\[f_k=\sum_vg_v[v\perp k]=\sum_{t\mid k}\mu(t)\sum_{t\mid v}g_v \]

使用若干 Dirichlet 前缀和即可 . 从而这一部分可以 \(O(nm\log m\log\log m)\) 解决 .

\(\bm{f\to g}\)

\[g_{i,j,k}=\sum_{v\mid k}f_{i,v,k}[v\perp j] \]

枚举 \(k\)，此处 \(j\) 的素因子集合 \(S_1\) 和 \(v\) 的素因子集合 \(S_2\) 的交集为空，可以考虑使用一些高维前缀和的技术解决（相当于是在 square-free 的整除格上考虑 Dirichlet 前缀和）.

这部分转移的时间复杂度是：

\[\begin{aligned}\sum_{k\le m}2^{\omega(k)}\omega(k)&\le\sum_{k\le m}d(k)\omega(k)\\&=\sum_{k\le m}\omega(k)\sum_{d\mid k}1\\&=\sum_{ik\le m}\omega(ik)\\&\le\sum_{ik\le m}(\omega(i)+\omega(k))\\&\sim\sum_{i\le m}\sum_{k\le m/i}\omega(i)\\&=O\left(\sum_{i\le m}\dfrac mi\log\log \dfrac mi\right)\\&=O(m\log m\log\log m)\end{aligned} \]

所以总共的时间复杂度是 \(O(nm\log m\log\log m)\) .

综合上述两部分，整个问题被 \(O(nm\log m\log\log m)\) 解决 .

CF868G El Toll Caves

让我这种除了无脑推式子啥都不会的选手很舒适，Solution .

[COTS 2025] 观草 / Trava

首先拆 \(x=V-\sum_k[x<k]\)，那么对于一个固定的 \(k\) 来说相当于就是令 \([a_i>k]\) 中间的空隙长度为 \(l_{1\dots m}\)，则答案为 \(\sum\min(l_i-k+1,0)\)，这个在值域上用树状数组就可以计算了 .

这里有一个类似支配对的结构：满足存在 \(k\) 使得 \(a_i,a_j>k\) 且 \(a_{i+1\dots j-1}\le k\) 的二元组 \((i,j)\) 只有 \(O(n)\) 个 . 具体可以考虑对于一对 \((i,j)\) 要么 \(i\) 是 \(j\) 前面第一个比它大的数、要么 \(j\) 是 \(i\) 后面第一个比它大的数 . 对于每个 \((i,j)\) 可以算出来对应 \(k\) 的取值区间，进而可以计算答案 .

支配对可以由构造过程单调栈找 . 对于单点修改来说，线段树二分到以 \(k\) 为端点的区间更新贡献即可 .

时间复杂度 \(O((n+q)\log n)\) .

CF1270I Xor on Figures

(GDKOI 染色)'s trick，其实和那个题基本上没啥区别 .

首先拆位在 \(\mathbb F_2\) 上做，后面懒得写了直接看染色题解，然后就 \(\Theta(tk4^k\log A)\) 了，结果过不了 \(k=9\) .

然而你冷静一下就可以发现其实可以不用拆位，\(\Theta(tk4^k)\) 即可通过 .

CF924F Minimal Subset Difference

判定：\(f_i\) 表示能不能得到 \(i\)，每次 \(f_i\to f_{i+c},\,f_i\to f_{|i-c|}\) .

取背包上界为 90，状态数只有 19185 . 搜出来大力 DP 套 DP 就可以了 .

[PA 2019 Final] 一安在？ / Gdzie jest jedynka? 2

玄学题，步数根本无法分析，只能玄学。。

特判 \(n=3\)，接下来对于一个位置 \(i\) 问出它和别的所有数的 GCD，这样 0 一定在 GCD 的最大值处，递归进入可以在 \(n\cdot O(1)\) 次操作内将 0 的位置确定到两个数中的一个 .

最后剩两个数，把第一轮的集合拿出来如果某个数跟这两个数的 GCD 都是 1 那么它就是 1，注意如果过程中确定两个数中的一个一定不是 0 就排除 .

QOJ #9459. Tree Equation

失去所有能力和手段

QOJ #9986. Shiori

首先显然只需要暴力找出 mex 以下的所有数，这样均摊下来复杂度也是对的 .

\(v\) 从 0 往上扫，每次线段树找出 \(=v\) 的连续段赋值为无穷大后查区间最小值即可找到区间内 \(>v\) 的最小数，当发现值域不连续的时候就找到了 mex .

通过一些简单的分析可以知道上述流程的时间复杂度为 \(O((n+q)\log^2n)\) .

UOJ #984. 欢迎来到最前线

从顺序匹配的角度看，把 \(a,b\) 放到一起排序，\(dp_{i,j}\) 表示考虑 \(1\dots i\) 配对 \(j\) 对的答案，每次转移只可能是不选和选一段 \(a,b\) 数量相等的段顺序匹配（调整可证）. 那么每个匹配区间只可能包含和在端点处相交，可以建出某种意义上的括号树结构 . 通过讨论可以发现每层独立，关于层内可以使用经典反悔贪心解决，层间使用 Minkowski 和合并即可 .

Remark. 其实可以不用树结构，直接考虑匹配的链结构（图源官方题解）：

图片

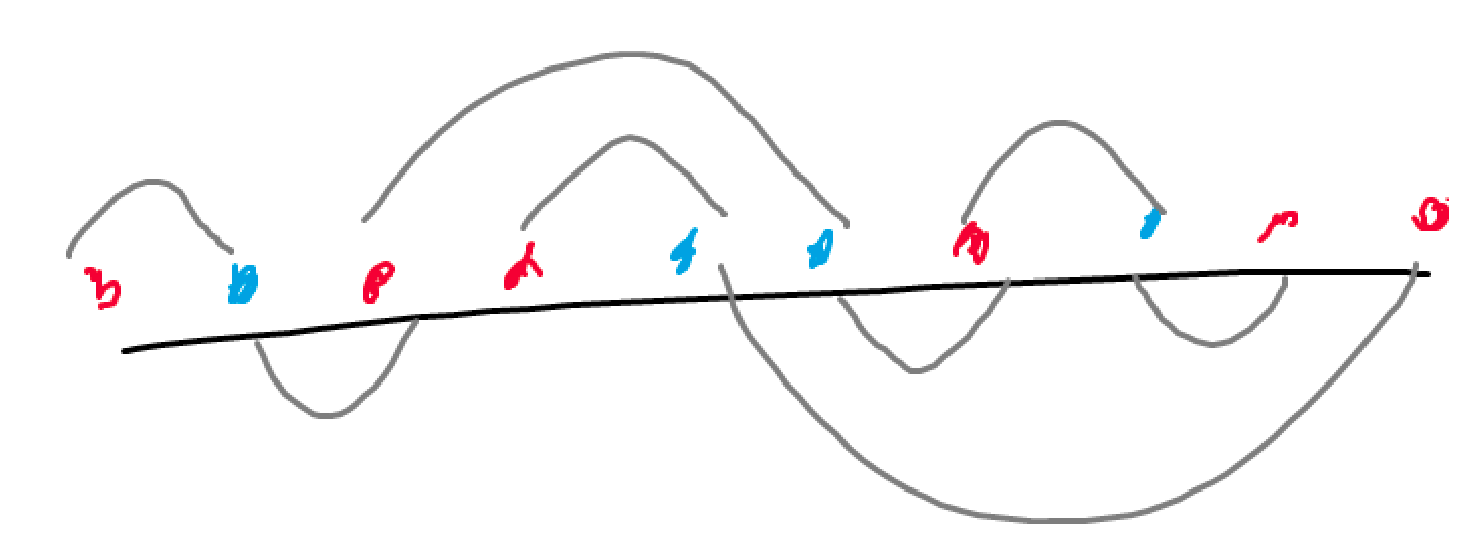
时间复杂度 \(O(n\log n)\) .

[JOI 2023 Final] 现代机器 / Modern Machine

口胡一波，感觉代码实现很不人道。。先咕着吧

操作大概就是根据左右的红 / 蓝色数讨论一波然后前 / 后缀染色什么的 . 如果有前 R 后 B 的性质可以考虑对分界点线段树维护函数复合（对数据结构的爱）. 如果没性质用 (鱼 2)'s trick，log 次必然就会到有性质的情况 .

CF1276E Four Stones

关于怎么判断无解：有解当且仅当 \(g=\gcd(a_2-a_1,a_3-a_1,a_4-a_1)=\gcd(b_2-b_1,b_3-b_1,b_4-b_1)\)，\(a_1\equiv b_1\pmod g\)，且做变换 \(x\to(x-d)/g\) 后 \(a,b\) 的奇 / 偶数个数相等 .

操作可逆，只需要同时走到中间状态——考虑把所有石头都放在相邻的两个位置 .

收缩 令 \(a\) 单调不降，\(\Delta\) 是极差 .

  • 如果存在 \(i\in[a_1+\frac\Delta4,a_4-\frac\Delta4]\)：把离 \(i\) 最近的石头翻过来，\(\Delta\) 至少减少 \(\frac\Delta4\) .
  • 如果不存在：把 \(a_2\) 先沿 \(a_3\) 再沿 \(a_4\) 翻转可以让 \(a_2-a_1\) 增加 \(2(a_4-a_3)\)，\(a_3\) 同理 . 那么每次选小的一边操作即可在 \(\Theta(\log\Delta)\) 步转为上一个情况 .

扩张 每轮 \(a_2\) 沿 \(a_4\) 翻转、\(a_3\) 沿 \(a_1\) 翻转，这样 \(\Delta\) 至少乘 2 .

平移 将 \(a\) 整体平移 \(\Delta\) 是平凡的，利用扩张就可以快速平移了 .

由此整个问题可以 \(O(\log V)\) 步解决 .

[PA 2020] Miny

\(dp_i\) 表示考虑 \(1\dots i\) 且钦定 \(i\) 不爆炸的答案，如果位置 \(j\) 满足 \((j,i)\) 中的地雷都无法引爆 \(i,j\)，则做转移 \(j\to i\) .

关于转移的限制，只要求出每个点左边最右的能引爆它的地雷和右边最左的能引爆它的地雷即可转为二维偏序，扫描线即可 . 时间复杂度 \(O(n\log n)\) .

CF1053E Euler tour

首先显然一个序列合法当且仅当可以通过做 \(x\,y\,x\to x\) 缩到只剩一个元素 . 对于原问题处理的方法是：

  • 如果有两个极近的填好的数 \(a_l=a_r=x\)，递归进入 \((l,r)\) .
  • 如果区间内的颜色数不够就在开头加点 .
  • 如果有 \(x\,y\,x\) / \(x\,y\,0\) / \(0\,y\,x\) 模式就缩掉 .
  • 如果还有 0 就填充上根结点 .

这样就可以了 . 过程中需要仔细判一下无解，缩点可以使用链表维护 . 时间复杂度 \(\Theta(n)\) .

[JOI 2016 Final] 铁路票价 / Train Fare

首先改边权可以看成删边 . 接下来 BFS 一下维护每个点在最短路 DAG 上的前驱，删边的时候统计出所有最短路改变的点删掉 . 根据均摊分析可得时间复杂度 \(\tilde O(m)\) .

UOJ #986. Sing

省流：\(p_i\le i+2(k+1)\)，对于 \(p_i\le i+k\) 没有任何限制，否则有一点限制 . \(dp_{i,j}\) 表示考虑 \(1\dots i\)，\(\le i+k\) 的数还有 \(j\) 个没有使用，每次转移的时候排列数算一下被限制到的区间的方案数 .

[AGC046E] Permutation Cover

首先显然有解当且仅当 \(2\min(a)\ge2\max(a)\) .

考虑增量构造：枚举长度 \(l\le k\) 并尝试向答案序列后加入一个长度为 \(l\) 的序列，使得后 \(k\) 位是一个排列 .

首先这 \(l\) 个元素组成的集合显然是确定的，考虑去掉这 \(l\) 个元素后的出现次数序列 \(a'\)：

  • \(2\min(a')\ge\max(a')\)：没有任何限制，从小到大填就完了 .
  • \(2\min(a')+1<\max(a')\)：无力回天了，这个 \(l\) 根本不合法跑路吧 .
  • \(2\min(a')+1=\max(a')\)：此时关键在于 \(\min(a')\) 对应的元素必须放在 \(\max(a')\) 对应的元素后面，简单贪心即可 .

由此可 \(O(k^2\sum a)\) 解决 .

CF1227G Not Same

什么构造全都不存在的，瞎几把随机化直接过了（

首先把每个数全 -1 预留一位值域，那么每次有两种策略：

  1. 找一个（=0，但是由于 -1 实际上 =1）的预留位置，把它和其他 >0 的位置一起 -1 .
  2. 找一个 >0 的位置，假装把它 -1（实际上不操作，留着最后操作），同时其他 >0 的位置 -1 .

不断操作直到序列归零，然后最后把第一种策略没用到的预留位置 -1，以及把第二种策略预留的操作做了即可 . 注意这里 2 操作选的位置每次都必须不一样，实现上可以按 \(a\) 升序排序从左往右选 . 如果成功显然操作次数不大于 \(n+1\) .

然而这个策略可能会有一点微小的问题：最后操作的两下可能会重复，同时有时候可能会没有位置可选 . 那么先做一次优先 1 的、再做一次优先 2 的、然后每轮随机选 1/2 直到找到合法解 . 虽然感觉根本没有任何道理，但是这样就可以过了：Submission .

CF341E Candies Game

重要观察：三个数一定有解 .

令三个数 \(0<a_x\le a_y\le a_z\)，若 \(a_x=1\) 那么把 \(a_y\) 二进制拆分，对应 1 的位置操作 \((x,y)\) 否则操作 \((x,z)\) 即可将 \(a_y\) 归零 . 若 \(a_x>1\) 用类似的操作可以让 \(a_y\gets a_y\bmod a_x\)，递归进入即可 . 对于更多的数只需要每三个操作一下就可以了 . 由 Euclid 算法可得时间复杂度为 \(O(n\log^2A)\) .

CF538G Berserk Robot

省流：首先转 45 度转为 1 维问题，接下来可以通过一些手段列出一系列关于一轮引发位移的方程，仔细求解即可 .

不等式除正数不变号除负数变号不能除 0 大于不大于向下取整小于不小于向上取整

QOJ #8542. Add One 2

一个最终状态 \(x\) 什么时候合法？倒着考虑每个操作，若 \(x_i>x_{i+1}\) 那么此处至少要进行 \(x_i-x_{i-1}\) 次前缀 -1，另一侧同理 . 如果最后得到全相等的序列后每个元素非负则合法 .

在开头和结尾加入足够大的元素 \(x_0-x_{n+1}=M\)，则合法当且仅当 \(x_0\ge\sum_{i=1}^n\max(0,x_i-x_{i+1})\) .

考虑到此时 \(\sum_{i=1}^n\max(0,x_i-x_{i+1})=\sum_{i=1}^n\max(0,x_{i+1}-x_i)\)，从而相加可得：

\[\sum_{i=0}^n|x_{i+1}-x_i|\le 2M \]

从而原问题即为每次可以选一个 \(a_i\) 加一要求到达一个满足上述条件的状态 . 注意到每次选中一个颜色段 \(a_{l\dots r}\) 使得 \(a_{l-1}>a_l,\,a_{r+1}>a_r\)，将它 +1 可以让左式 -2 . 那么在笛卡尔树上从短到长依次操作每个颜色段并且动态维护颜色段合并即可 . 时间复杂度 \(O(n)\) .

CF1017G The Tree

如果没有 2 操作的话，可以考虑在每个点上维护它被进行的 1 操作次数 -1，那么 \(x\) 为黑色当且仅当其根链的最大后缀和 \(\ge 0\) . 对于 2 操作来说，首先清空它子树内的所有 1 操作，接下来把操作位置上方晕染下来的黑色吸回去，相当于进行负数次的 1 操作 . 总之只需要支持子树赋值、单点修改、查询根链最大后缀和，使用树剖 + 线段树维护即可 .

时间复杂度 \(O(n+q\log^2n)\) . 用手法可以 \(O(n+q\log n)\) 甚至 \(O(n+q\frac{\log^2n}{\log\log n})\) .

[PA 2024] Bardzo Ulubiony Ciąg

太笨蛋了啊，一维偏序扫描线天然维护啊。。

QOJ #8543. Periodic Sequence

对于答案序列 \(S\)，如果 \(|S_1|\neq n\) 就在开头加一个合法串（如果找不到不重复的，加重复的也可以）. 接下来可以归纳得出存在一簇字符串 \(T_{1\dots k}\sqsubseteq S_1\)（其中 \(|T_1|=\max|T_i|\)）使得每个 \(S_i\) 都是若干 \(T_i\) 的拼接 . 那么可以简单得到一个答案的上界：正整数序列 \(\{x\}\text{ s.t. }\sum x_i\le n,\,x_1=\max x_i\) 的个数 .

构造：令字符串长度 \(\le i\) 的答案为 \(Q_i\)，增量构造：

  • \(Q_1=\{\texttt{a}\}\) .
  • 在 \(Q_{i-1}\) 的每个字符串后面加一个合法的长度为 \(i\) 的字符串，如果有重复只加前面位置的那个 . 然后在开头加一个长度为 \(i\) 的串 \(\texttt{ab}\dots\texttt{b}\) 得到 \(Q_i\) .

归纳可证此构造可以使得字符串序列和 \(\{x\}\) 序列双射，从而上述上界即为答案 .

那么问题转为求

\[\dfrac1{1-x}\sum_{k\ge1}\dfrac{x^k}{1-\frac{x-x^{k+1}}{1-x}}=\sum_{k\ge1}\dfrac{x^k}{1-2x+x^{k+1}} \]

对 \(k\) 根号分治：

  • \(k\le\sqrt n\)：暴力求 \(\sqrt n\) 次逆 .
  • \(k>\sqrt n\)：考虑写为

    \[\sum_{k\ge1}\dfrac{x^k}{1-2x+x^{k+1}}=\sum_{k\ge1}\dfrac{x^k}{(1-2x)(1+\frac{x^{k+1}}{1-2x})} \]

    把 \((1+\frac{x^{k+1}}{1-2x})^{-1}\) 展开掉，最多产生 \(\sqrt n\) 项，然后交换一下求和号就可以算了 .

综上可以 \(O(n\sqrt n)\) 完成 . 如果利用 \(\sqrt n\times\sqrt n=n\) 使用分治乘维护上述过程可以 \(O(n\log^2n)\)（详见 zak 博客）.

[CCO 2020] Shopping Plans

（省流）整体上用超级钢琴's trick 的思路，大致分为两个子问题：

  • \(m=1\)：如果 \(x_i=y_i\) 的话相当于每次转移把若干元素右移若干位，由于有一定的支配关系可以改成每次右移一位或者切换进入下一个元素，这样每个状态只有 2 个后继位置 . 对于 \(x_i,y_i\) 任意的情况其实是一样的 .
  • \(x_i=y_i=1\)：转移就是每次选一个种类然后让它里面的元素右移一点，可以用类似三度化的 trick 让度数变成 \(O(1)\) 的，这样就可以做了 .

对于原问题来说，种类间用 \(x_i=y_i=1\) 的做法、种类内用 \(m=1\) 的做法就可以了，时间复杂度 \(O(n\log n)\) .

可以看看 cmd 题解 或者 wsc 题解，有图片 .

CF1442D Sum

调整可证最多 1 个选了元素的序列不选满，然后用缺一分治随意维护一下就可以 \(O(nk\log n+\sum t_i)\) 了 .

[NOI2022] 众数

随机化彻底爆了。。

贺个分治做法：将序列随意分成两部分，其中必有一部分的绝对众数是原序列的绝对众数，可以分治 . 外层用启发式合并 map 会变成 2 log 不过也可以过 .

[JOI Open 2018] 猫或狗 / Cats or Dogs

动态 DP：\(f_{u,c}\) 表示点 \(u\) 所在连通块颜色为 \(c\) 的答案……

唉感觉静态 Top Tree 做起来好烦啊。。一堆细节得讨论

[Ynoi2009] rprmq1

因为好像网上还没人破解标题我就煞有介事地破解一下：rprmq = rectangle plus rectangle maximum query

如果扫一维改成动态问题就相当于区间加，某一时间段内的区间历史最大值 . 可以看成对于每个起点出发的普通历史最大值，对时间轴猫树分治之后使用线段树维护区间加区间历史最值即可（其实线段树可以打个标记清空历史最值）.

如果返回来看其实开局不用改成动态问题，可以直接对一维猫树分治，不过可能会不太容易理解 .

时间复杂度 \(O(n\log^2n+q\log n)\) .

posted @ 2025-05-10 17:20  yspm  阅读(155)  评论(2)    收藏  举报
😅​