可持久化线段树

值域线段树

设线段树节点 $i$ 管辖区间 $[l,r]$，$i$ 的 $val$ 表示 $ l\ge $ 且 $ \le r$ 的数的个数
那么 $i.l$ 表示$ l\ge $ 且 $ \le mid$ 的数的个数， $i.r$ 表示$ mid+1\ge $ 且 $ \le r$ 的数的个数
如果建 $n$ 棵值域线段树，第 $i$ 棵维护区间 $[1,i]$，那么查找 $[l,r]$ 区间的第 $k$ 大就将第 $r$ 棵树与第 $l-1$ 棵树相减，得到的就是 $[l,r]$ 的信息（有点像差分哈）
但是第 $i$ 棵树与第 $i-1$ 棵树的差别很小，可以只记录两棵树之间的差别

可持久化线段树

操作：
- Update
- Query
每次的Update就是在值域上加入一个点，只新建了一条长度为 $log_2 n$ 的链，于是新的树就是在原树的基础上添加了一条链，其余的节点的信息直接复制过去就行

图片来自博客园
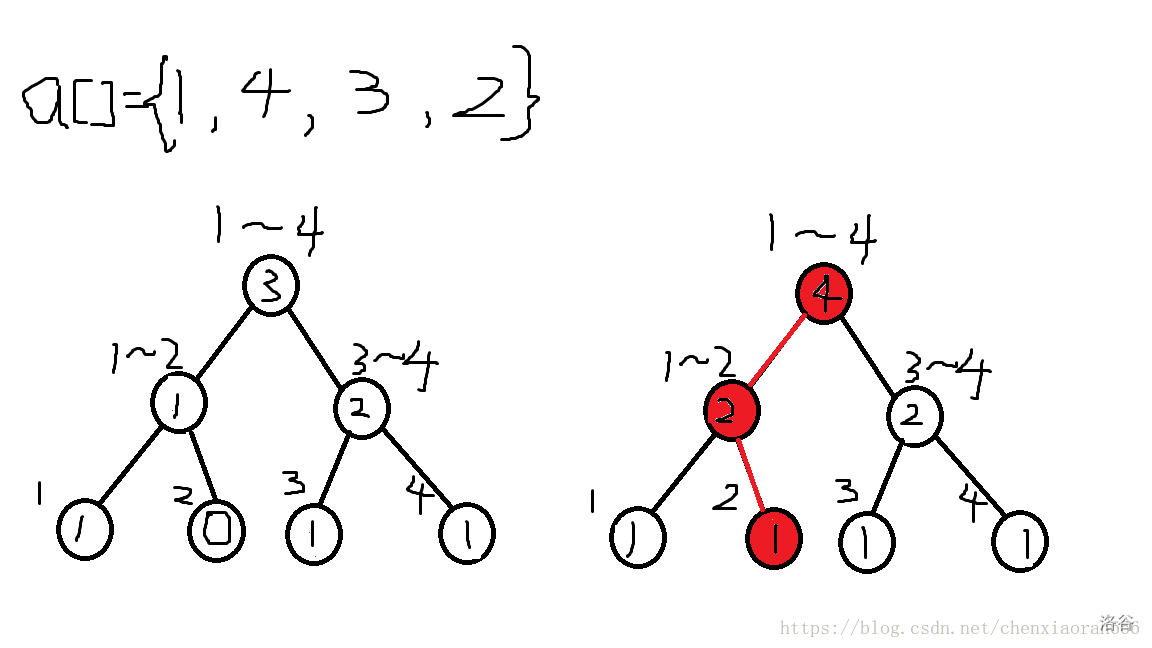
红色的链就是插入 $2$ 后新增的

int Update(int pre,int l,int r,int val){
    int rt=++cnt;   //动态开点
    t[rt].cnt=t[pre].cnt; t[rt].l=t[pre].l; t[rt].r=t[pre].r;   //复制节点信息
    t[rt].cnt++;
    int mid=(l+r)/2;
    if(l<r){
        //连接新增的节点（将t[rt].l/t[rt].r与他们的新子节点连接）
        if(val<=mid) t[rt].l=Update(t[pre].l,l,mid,val);
        else t[rt].r=Update(t[pre].r,mid+1,r,val);
    }
    return rt;
}

for(int i=1;i<=n;i++){
    int pos=lower_bound(rk+1,rk+1+siz,in[i])-rk;
    rt[i]=Update(rt[i-1],1,siz,pos);    //记录这次修改的根节点
}

图片来自博客园
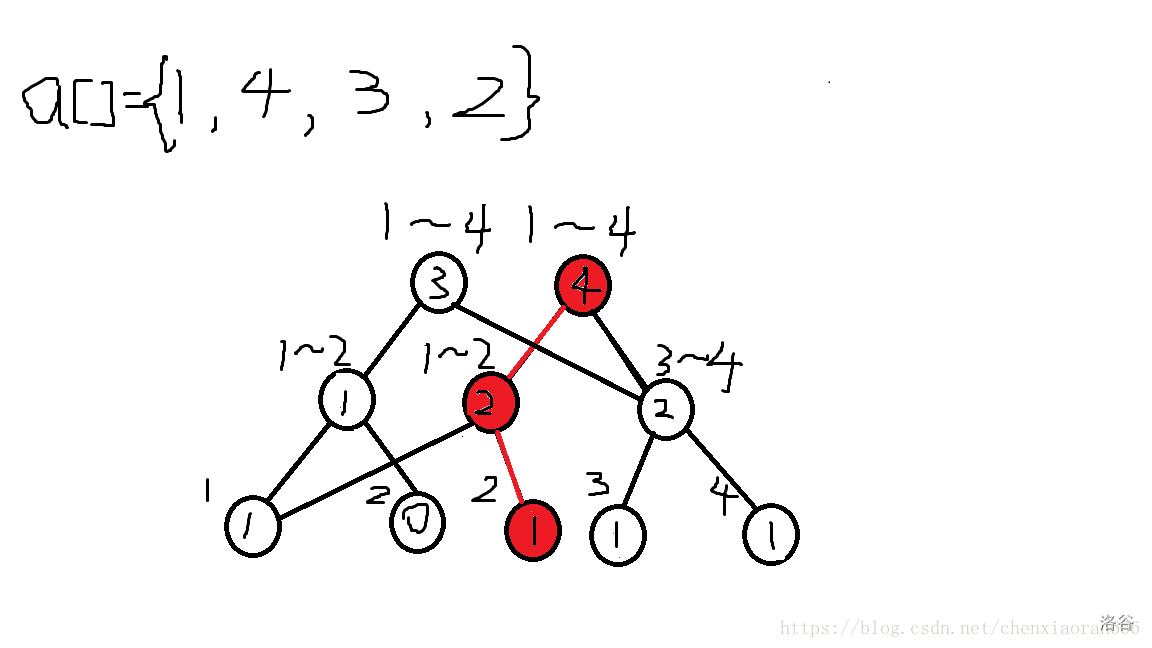
修改后新加上的链并在原来的树上，成了这个样子
Query操作将树 $now$ 的信息减去树 $l-1$ 的信息得到 $[l,r]$ 的信息

int Query(int pre,int now,int l,int r,int k){
    if(l==r) return l;
    int cnt=t[t[now].l].cnt-t[t[pre].l].cnt;
    int mid=(l+r)/2;
    if(cnt>=k)
        return Query(t[pre].l,t[now].l,l,mid,k);
    else 
        return Query(t[pre].r,t[now].r,mid+1,r,k-cnt);
}

for(int i=1;i<=m;i++){
    cin>>l>>r>>k;
    int pos=Query(rt[l-1],rt[r],1,siz,k);
    cout<<rk[pos]<<"\n";
}

因为开的是值域线段树，所以如果值域很大（比如这题的 $10^9$ ），需要离散化一下

https://www.luogu.com.cn/problem/P3834

区间第 $k$ 大/小问题
方法同上面

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10;

int n,m,siz;
int in[N],rk[N],l,r,k;
struct Node{
    int l,r,cnt;
}t[N<<5];
int cnt,rt[N];

int Update(int pre,int l,int r,int val){
    int rt=++cnt;
    t[rt].cnt=t[pre].cnt; t[rt].l=t[pre].l; t[rt].r=t[pre].r;
    t[rt].cnt++;
    int mid=(l+r)/2;
    if(l<r){
        if(val<=mid) t[rt].l=Update(t[pre].l,l,mid,val);
        else t[rt].r=Update(t[pre].r,mid+1,r,val);
    }
    return rt;
}

int Query(int pre,int now,int l,int r,int k){
    if(l==r) return l;
    int cnt=t[t[now].l].cnt-t[t[pre].l].cnt;
    int mid=(l+r)/2;
    if(cnt>=k)
        return Query(t[pre].l,t[now].l,l,mid,k);
    else 
        return Query(t[pre].r,t[now].r,mid+1,r,k-cnt);
}

signed main(){
    // freopen("1.in","r",stdin);
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>in[i];
        rk[i]=in[i];
    }
    sort(rk+1,rk+1+n);
    siz=unique(rk+1,rk+1+n)-rk-1;
    for(int i=1;i<=n;i++){
        int pos=lower_bound(rk+1,rk+1+siz,in[i])-rk;
        rt[i]=Update(rt[i-1],1,siz,pos);
    }
    for(int i=1;i<=m;i++){
        cin>>l>>r>>k;
        int pos=Query(rt[l-1],rt[r],1,siz,k);
        cout<<rk[pos]<<"\n";
    }
}

https://www.luogu.com.cn/problem/P3919

区间更新问题
操作类似，每次操作会产生一个新版本

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10;

int n,m;
int in[N],edit,opt,loc,val;
struct Node{
    int l,r,val;
}t[N<<5];
int cnt,rt[N];

void Clone(int now,int pre){
    t[now].l=t[pre].l;
    t[now].r=t[pre].r;
    t[now].val=t[pre].val;
}

int Build(int l,int r){
    int rt=++cnt;
    if(l==r){
        t[rt].val=in[l];
        return rt;
    }
    int mid=(l+r)/2;
    t[rt].l=Build(l,mid);
    t[rt].r=Build(mid+1,r);
    return rt;
}

int Update(int id,int l,int r,int loc,int val){
    int rt=++cnt;
    Clone(rt,id);
    if(l==r){
        t[rt].val=val;
        return rt;
    }
    int mid=(l+r)/2;
    if(loc<=mid) t[rt].l=Update(t[id].l,l,mid,loc,val);
    else t[rt].r=Update(t[id].r,mid+1,r,loc,val);
    return rt;
}

int Query(int id,int l,int r,int loc){
    if(l==r)
        return t[id].val;
    int mid=(l+r)/2;
    if(loc<=mid) return Query(t[id].l,l,mid,loc);
    else return Query(t[id].r,mid+1,r,loc);
}

signed main(){
    // freopen("1.in","r",stdin);
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>in[i];
    rt[0]=Build(1,n);
    for(int i=1;i<=m;i++){
        cin>>edit>>opt>>loc;
        if(opt==1){
            cin>>val;
            rt[i]=Update(rt[edit],1,n,loc,val);
        }else{
            cout<<Query(rt[edit],1,n,loc)<<"\n";
            rt[i]=rt[edit];
        }
    }
}

https://www.luogu.com.cn/problem/P4587

逐个枚举每个可能的神秘数
假设现在可以表示出神秘数 $[1,x]$，那么如果添加集合 $S$ 的元素 $k$：
- $k \le x+1$，那么现在可以表示 $[1,x] \cup [1+k,x+k] = [1,x+k]$
- $k \gt x+1$，那么可以表示的数的集合不连续，最小的非神秘数就是 $x+1$
优化一下：
- 如果值域在 $[1,x]$ 的集合 $S$ 的元素能表示神秘数 $[1,y]$，那么放进去 $[1,y+1]$ 的数都是合法的
- 值域在 $[1,x]$ 的数能表示的神秘数的和为 $i=sum([1,x])$，值域在 $[1,y+1]$ 的数能表示的神秘数的和为 $j=sum([1,y+1])$，如果 $i < j $，则区间 $[1,y]$ 中有 $j-i$ 的数还没用，把他们都放进去，现在能表示的神秘数变为 $[1,j]$
- 求和的事情用主席树来干就行

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int INF=1e9+10;
const int N=1e6+10;

int n,m;
int in[N],l,r;
struct Node{
    int l,r,val;
}t[N<<5];
int cnt,rt[N];

int Update(int pre,int l,int r,int val){
    int rt=++cnt;
    t[rt]=t[pre]; t[rt].val+=val;
    if(l==r) return rt;
    int mid=(l+r)/2;
    if(val<=mid) t[rt].l=Update(t[pre].l,l,mid,val);
    else t[rt].r=Update(t[pre].r,mid+1,r,val);
    return rt;
}

int Query(int pre,int now,int l,int r,int ql,int qr){
    if(ql<=l && r<=qr) return t[now].val-t[pre].val;
    int mid=(l+r)/2,ans=0;
    if(ql<=mid) ans+=Query(t[pre].l,t[now].l,l,mid,ql,qr);
    if(qr>mid) ans+=Query(t[pre].r,t[now].r,mid+1,r,ql,qr);
    return ans;
}

signed main(){
    // freopen("1.in","r",stdin);
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>in[i];
        rt[i]=Update(rt[i-1],1,INF,in[i]);
    }
    cin>>m;
    for(int i=1;i<=m;i++){
        cin>>l>>r;
        int ans=1,res;
        while(true){
            res=Query(rt[l-1],rt[r],1,INF,1,ans);
            if(res>=ans) ans=res+1;
            else break;
        }
        cout<<ans<<"\n";
    }
}

posted on 2023-05-10 20:05 Bubble_e 阅读(31) 评论(0) 收藏举报

刷新页面返回顶部