CF932C Permutation Cycle

题目传送门

思路：

个人认为构造题全靠感性理解，理解对了问题就迎刃而解了。（有点像做阅读理解）

我们先感性地理解题目中所有变量和函数的含义。

\(f\) 函数是什么？

当 \(j \neq 0\) 时，\(f(i, j) = f(p_i, j - 1)\)，就是使 \(j\) 花费了 \(1\) 的代价，然后使 \(i\) 变为了 \(p_i\)。

这就可以联想到在一张图上移动，那么 \(f(i, j)\) 中的 \(j\) 就相当于剩余步数，\(i\) 就相当于目前的位置。

那么当 \(j = 1\) 时也可以这样来解释。

注意到每次移动为 \(i \rightarrow p_i\)，可以理解为 \(i\) 向 \(p_i\) 连了一条有向边，那么 \(p\) 数组的含义也就得以解释。

将整个问题放在一张有向图上，所以 \(f(i, j)\) 表示从点 \(i\) 出发，走 \(j\) 步到达的点的编号，这恰好印证证了 \(1\le p_i\le n\) 这一条件。

\(G\) 数组是什么？

根据我们对 \(f\) 函数的定义，那么 \(G\) 数组的含义即为：从 \(i\) 出发走回到点 \(i\) 的最小步数。

综上所述，问题变成了：构造一个含有 \(n\) 个点的有向图，使得图中每个点都能在走 \(A\) 步或 \(B\) 步后回到原点。

手玩一下样例一，发现它构造的有向图如下：

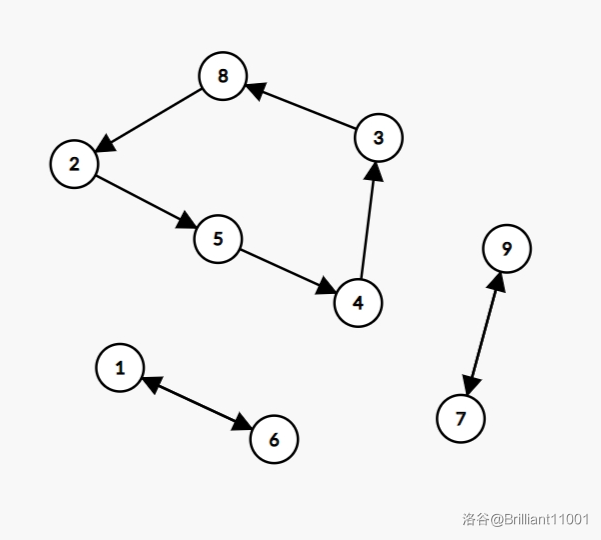
发现是一个长度为 \(5\) 的环和两个长度为 \(2\) 的环！

从中我们可以得到启发：在图中构造两种环，一种长度为 \(A\)，一种长度为 \(B\)。

设构造了 \(x\) 个长度为 \(A\) 的环，\(y\) 个长度为 \(B\) 的环。

所以解不定方程：

\[Ax + By = n \]

即可。

其中 \(x,y\) 都为非负整数。

由于输出一种方案即可，数据范围也不大，可以暴力枚举 \(x\)。

最后构造就行了。

\(\texttt{Code:}\)

#include <iostream>
using namespace std;

const int N = 1000010;

int n, a, b;
int p[N];

int main() {
    scanf("%d%d%d", &n, &a, &b);
    bool flag = false;
    int x, y;
    for(x = 0; x <= n / a; x++) //枚举 x
        if((n - x * a) % b == 0) {
            flag = true;
            y = (n - x * a) / b;
            break; //随便找一个解
        }
    if(!flag) puts("-1"); //找不到解
    else {
        int id = 1;
        for(int i = 1; i <= x; i++) { //构造 x 个长度为 a 的环
            for(int j = 1; j < a; j++)
                p[id] = id + 1, id++;
            p[id] = id - a + 1, id++;
        }
        for(int i = 1; i <= y; i++) { //构造 y 个长度为 b 的环
            for(int j = 1; j < b; j++)
                p[id] = id + 1, id++;
            p[id] = id - b + 1, id++;
        }
        for(int i = 1; i <= n; i++) printf("%d ", p[i]);
    }
    return 0;
}

总结一下如何做构造题（仅供参考）：

1. 先理解清楚题中每个定义的含义；
2. 根据定义大胆发挥联想；
3. 从样例和样例解释找灵感。