最实用之数据结构思想——分块

前言

虽然分块是一种数据结构，但是我认为它更像一种思想：分部分处理序列。

虽然分块的时间复杂度一般比树状数组和线段树高，但是它能解决很多树状数组和线段树解决不了的事情。比如：树状数组和线段树在维护不满足区间可加、可减性的信息时显得吃力，代码实现也不简单直观。这时候，常常就要请出我们的分块大法啦。

它更通用、更容易实现，也更加直观。（这就是时间复杂度越高的算法越通用）它实际上是一种优雅的暴力。

简介：

分块，顾名思义，就是将一个序列分成几块，然后对于修改和询问有技巧地整合各块的信息。这里的技巧就是分块的核心思想：“大段维护，小段朴素”。

分块的划分也具有一定的策略，但始终遵循一个原则：“化学反应速率原理” 整个程序的时间复杂度取决于时间复杂度最高的一步，所以要做到合理地分块，预处理一部分信息并保存下来，用空间换取时间，达到时空平衡，才能达到降低时间复杂度的目的。

【模板】 线段树 1

这里还是一这道题为例，区间修改 + 区间询问。

我们先来想想如何分块才能最快。

假设将原序列分成 \(L\) 段，每段的元素个数是 \(N / L\)，对于每次操作，若整个块都被包含，就改变整个块；若未被全部包含，就朴素修改。所以每次修改操作的时间复杂度为 \(O(L + \frac{2N}{L})\)，也就是 \(O(L + \frac{N}{L})\) ，根据基本不等式，可得：

\[L + \frac{N}{L} \ge \sqrt{N} \]

当且仅当 \(L = \frac{N}{L}\) 即 \(L = \sqrt N\) 时等号成立。

所以，当我们将原序列分成 \(\sqrt N\) 块时，时间复杂度最优。

比如，对于一个长度为 \(10\) 的序列，将它这样划分：

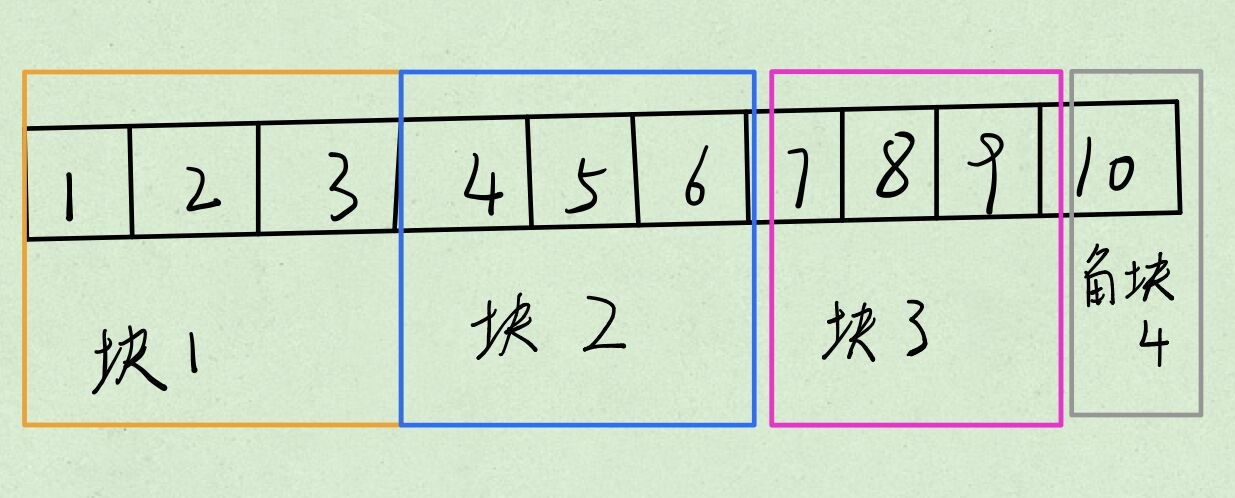
对于第 \(i\) 个块，其左端点为 \((i - 1)\lfloor \sqrt N \rfloor + 1\)，右端点为 \(\min(i\lfloor \sqrt N \rfloor,N)\)。

可以用如下代码记录每块的左右端点：

for(int i = 1; i <= t; i++) L[i] = (i - 1) * sqrt(n) + 1, R[i] = i * sqrt(n);
if(n > R[t]) t++, L[t] = R[t - 1] + 1, R[t] = n;

另外，预处理出区间和数组 \(sum\)，表示第 \(i\) 块的区间和。设 \(add[i]\) 表示第 \(i\) 块的”增量标记“，初始化为 \(0\)。（学过线段树的话这个应该还好理解）

区间修改

对于区间加指令 \(\texttt{“C l r d”}\)：

1. 若 \(l\) 和 \(r\) 同时处于第 \(i\) 段内，就直接朴素修改，将 \(A[l],A[l + 1],\cdots,A[r]\) 都加上 \(d\)，同时令 \(sum[i] += d*(r - l + 1)\)。

2. 否则，设 \(l\) 处于第 \(p\) 段，\(r\) 处于第 \(q\) 段。

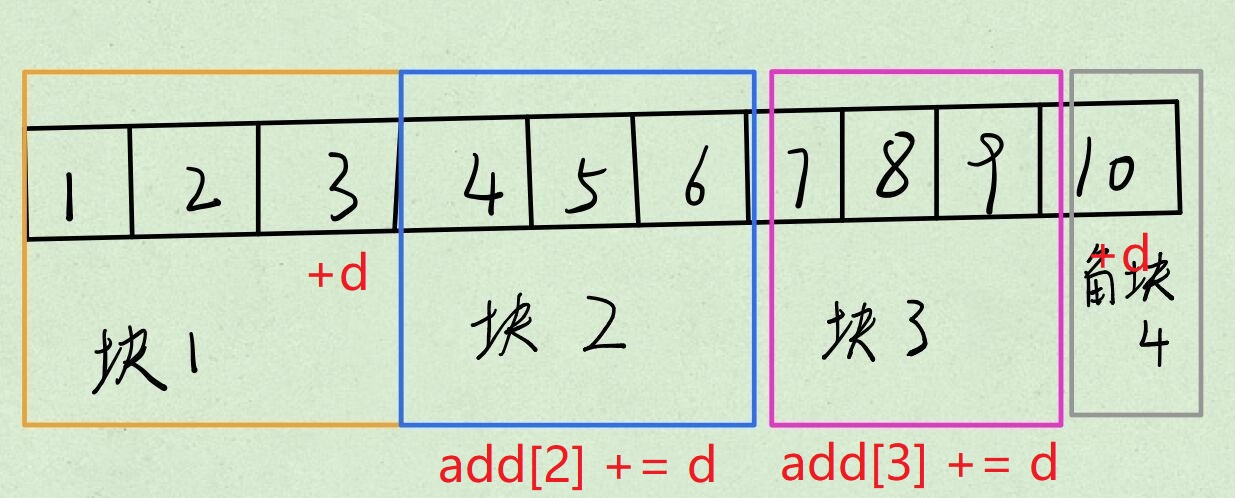
   (1) 对于 \(i\in [p + 1, q - 1]\)，令 \(add[i] += d\)。

   (2) 对于开头、结尾不足一整段的两部分，按照情况 \(1\) 的方法朴素修改。

比如要在区间 \([3,7]\) 上加上 \(5\)，就可以这样操作：

区间查询

对于区间查询指令 \(\texttt{“Q l r”}\)：

1. 若 \(l\) 和 \(r\) 同时处于第 \(i\) 段内，则 \((A[l] + A[l + 1] + \cdots + A[r]) + (r - l + 1) * add[i]\) 就是答案。

2. 否则，设 \(l\) 处于第 \(p\) 段，\(r\) 处于第 \(q\) 段，初始化 \(ans = 0\)。

   (1) 对于 \(i\in [p + 1, q - 1]\)，令 \(ans += sum[i] + add[i] * len[i]\)，其中 \(len[i]\) 表示第 \(i\) 段的长度。

   (2) 对于开头、结尾不足一整段的两部分，按照情况 \(1\) 的方法朴素累加。

由于段数和段长都是 \(O(\sqrt N)\)，所以整个算法的时间复杂度为 \(O((N + Q) * \sqrt N)\)

代码：

#include <iostream>
#include <cmath>

using namespace std;

const int N = 100010;
typedef long long ll;
int n, m, t;
ll a[N];
int L[N], R[N];
ll add[N], sum[N];
int pos[N];

void change(int l, int r, ll val) {
	int p = pos[l], q = pos[r];
	if(p == q) {
		for(int i = l; i <= r; i++) a[i] += val;
		sum[p] += (r - l + 1) * val;
	}
	else {
		for(int i = l; i <= R[p]; i++) a[i] += val;
		sum[p] += val * (R[p] - l + 1);
		for(int i = L[q]; i <= r; i++) a[i] += val;
		sum[q] += val * (r - L[q] + 1);
		for(int i = p + 1; i <= q - 1; i++) add[i] += val;
	}
}

ll query(int l, int r) {
	int p = pos[l], q = pos[r];
	ll res = 0;
	if(p == q) {
		for(int i = l; i <= r; i++) res += a[i];
		res += (ll)add[p] * (r - l + 1);
	}
	else {
		for(int i = l; i <= R[p]; i++) res += a[i];
		res += (ll)add[p] * (R[p] - l + 1);
		for(int i = L[q]; i <= r; i++) res += a[i];
		res += (ll)add[q] * (r - L[q] + 1);
		for(int i = p + 1; i <= q - 1; i++) res += (ll)add[i] * (R[i] - L[i] + 1) + sum[i];
	}
	return res;
}

int main() {
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i++) scanf("%lld", &a[i]);
	
	t = sqrt(n);
	for(int i = 1; i <= t; i++) L[i] = (i - 1) * sqrt(n) + 1, R[i] = i * sqrt(n);
	if(n > R[t]) t++, L[t] = R[t - 1] + 1, R[t] = n;
	for(int i = 1; i <= t; i++) {
		for(int j = L[i]; j <= R[i]; j++) {
			pos[j] = i;
			sum[i] += a[j];
		}
	}
	int op, x, y;
	ll k;
	while(m--) {
		scanf("%d%d%d", &op, &x, &y);
		if(op == 1) {
			scanf("%lld", &k);
			change(x, y, k);
		}
		else {
			printf("%lld\n", query(x, y));
		}
	}
	
	return 0;
}