速通初赛
1.快速排序
void qsort(int l, int r) {
int mid = a[(l + r) / 2];
int i = l, j = r;
do{
while(a[i] < mid) i++;
while(a[j] > mid) j--;
if(i <= j) {
swap(a[i], a[j]);
i++;
j--;
}
}while(i <= j);
if(l < j) qsort(l, j);
if(i < r) qsort(i, r);
}
2.归并排序
void mergesort(int l, int r) {
if (l == r) return;
int mid = (l + r) / 2;
int p = l, i = l, j = mid + 1;
mergesort(l, mid);
mergesort(mid + 1, r);
while (i <= mid && j <= r) {
if (a[j] < a[i]) {
s += mid - i + 1;
t[p++] = a[j++];
}
else {
t[p++] = a[i++];
}
}
while (i <= mid) t[p++] = a[i++];
while (j <= r) t[p++] = a[j++];
for (i = l; i <= r; i++) a[i] = t[i];
}
重点：
设 \(A\) 和 \(B\) 是两个长为 \(n\) 的有序数组，现在需要将 \(A\) 和 \(B\) 合并成一个排好序的数组，归并算法最坏情况下至少要做 \(2n - 1\) 次比较，最好情况下至少要做 \(n\) 次比较！
3.完全图
对于两个不同的节点，都恰好有一边相连的图。边数为 \(n * n(n - 1) / 2\)
4.Catalan数(卡特兰数)
卡特兰数是组合数学中一个常出现于各种计数问题中的数列。
\(Cat _ {n}\) 表示所有在 \(n × n\) 格点中不越过对角线的单调路径的个数。
通项公式：\(Catalan _ {n}\) = \(\frac{1}{n + 1}C _ {2n} ^ {n}\)
递推公式：\(Catalan _ {n}\) = \(\frac{4n + 2}{n + 2}Catalan _ {n - 1}\)
5.UNIX是操作系统！
6.MPEG是视频文件格式！
7.无向图不分入度和出度！无向图中点的度数和为边数的两倍！
8.同时查找 2n 个数中的最大值和最小值，最少比较次数为 \(3n - 2\)!
9.计算机网络
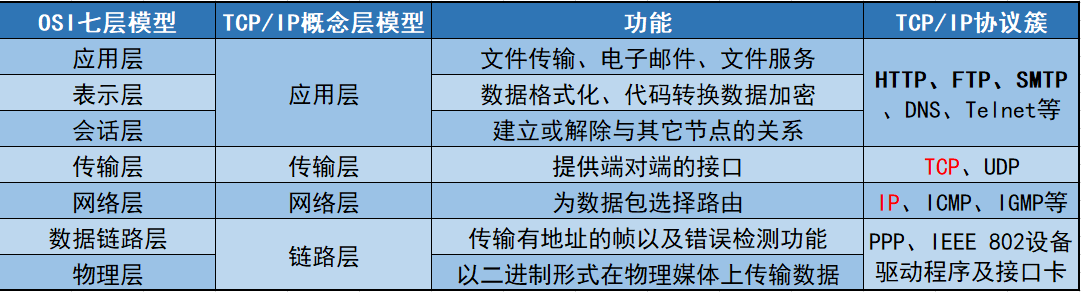
(1) ISO制定了OSI模型，将网络通信工作分成了七层，分别是物理层、数据链路层、网络层、传输层、会话层、表示层和应用层。
(2) TCP/IP协议:传输控制协议/网络协议
10.IP地址
形如 \(a.b.c.d\)，其中 \(a\)、\(b\)、\(c\)、\(d\)都为 \(8\) 位二进制数，即都是0~255之间的十进制整数！
A类地址：\(a∈[0,127]\)！
B类地址：\(a∈[128,191]\)！
C类地址：\(a∈[192,223]\)！
D、E类地址不常用！
11.Internet相关概念
