归一化（Normalization）

归一化（Normalization）是一种常见的数据预处理方法，用于将数据按比例缩放到某个特定的范围，以便于不同量纲或数量级的数据能够进行比较或综合分析。

常见的归一化方法

1. 最小-最大归一化（Min-Max Normalization）

将数据线性地缩放到一个指定的区间，通常是 [0, 1] 或 [-1, 1]。

公式如下（以 [0, 1] 为例）：

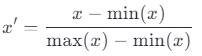
如果要缩放到 [-1, 1]，可以使用：

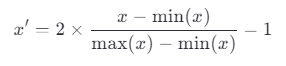
优点：

简单直观
保留原始数据分布形状
缺点：

对异常值敏感（极小值或极大值会影响整体缩放效果）

Java代码

public static double[] minMaxNormalize(double[] data, double newMin, double newMax) {
    double min = Arrays.stream(data).min().getAsDouble();
    double max = Arrays.stream(data).max().getAsDouble();
    return Arrays.stream(data).map(v -> (v - min) / (max - min) * (newMax - newMin) + newMin).toArray();
}

 

 2. Z-Score 标准化（Standardization）

虽然这不是严格意义上的“归一化”，但常被混用此术语。

公式：

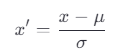
其中，μ 是均值，σ 是标准差。

特点：

数据中心变为 0，标准差为 1
不限制范围在 [-1, 1]，但如果数据近似正态分布，大多数值会在这个范围内
优点：

对异常值更鲁棒（相比 Min-Max）
适用于数据分布不均匀或存在极端值的情况

Java代码

public static double[] zScoreNormalize(double[] data) {
    double mean = Arrays.stream(data).average().orElse(0.0);
    double std = Math.sqrt(Arrays.stream(data).map(v -> v - mean).map(v -> v * v).sum() / data.length);
    return Arrays.stream(data).map(v -> (v - mean) / std).toArray();
}

3. 小数缩放归一化（Decimal Scaling）

通过移动小数点位置来进行归一化。

公式：

其中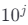是使得的最小幂次。

Java代码

public static double[] decimalScalingNormalize(double[] data) {
    double maxAbsValue = Arrays.stream(data).map(Math::abs).max().getAsDouble();
    int j = (int) Math.ceil(Math.log10(maxAbsValue));
    return Arrays.stream(data).map(v -> v / Math.pow(10, j)).toArray();
}

 

示例说明：

假设有一组数据：

原始数据：[10, 20, 30, 40, 50]

我们想把它归一化到 [-1, 1] 范围：

最小值 min = 10
最大值 max = 50

代入公式：

 

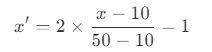
计算结果：

x=10 → x' = -1
x=20 → x' = -0.5
x=30 → x' = 0
x=40 → x' = 0.5
x=50 → x' = 1

 

Java 实现代码（[-1, 1] 范围）

 

import java.util.Arrays;

public class NormalizationExample {

    public static double[] normalizeToMinusOneToOne(double[] data) {
        if (data == null || data.length == 0) return new double[0];

        double min = Arrays.stream(data).min().getAsDouble();
        double max = Arrays.stream(data).max().getAsDouble();

        double[] normalized = new double[data.length];
        for (int i = 0; i < data.length; i++) {
            normalized[i] = 2 * (data[i] - min) / (max - min) - 1;
        }
        return normalized;
    }

    public static void main(String[] args) {
        double[] data = {10, 20, 30, 40, 50};

        System.out.println("原始数据: " + Arrays.toString(data));
        double[] normalizedData = normalizeToMinusOneToOne(data);
        System.out.println("归一化后: " + Arrays.toString(normalizedData));
    }
}

 

应用场景举例

场景一：深度学习中常见归一化方法

在深度学习中，通常要求输入特征在 [-1, 1] 或 [0, 1] 范围内。例如，在卷积神经网络（CNN）处理图像时，像素值一般被归一化为 [0, 1] 或 [-1, 1]。

归一化技术对于加速其训练过程、提高模型性能以及稳定训练过程至关重要。以下是一些常用的归一化方法及其简要介绍和应用场景：

1. 批量归一化（Batch Normalization）

定义与原理：
批量归一化是在神经网络的每一层输入之前进行的操作，它通过将每个小批次的数据规范化到均值为0，方差为1来减少内部协变量偏移的问题。

公式：

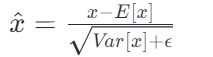
然后通过缩放和平移：

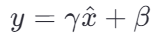
其中，E[x] 和Var[x] 分别是小批次中的均值和方差，ϵ 是为了数值稳定性而添加的小常数，γ 和β 是可学习参数。

应用场景：
适用于大多数类型的神经网络，特别是卷积神经网络（CNNs）和前馈神经网络（Feedforward Neural Networks）。有助于加速训练，并允许使用更高的学习率。

2. 层归一化（Layer Normalization）

定义与原理：
层归一化是对单个样本的所有特征进行归一化处理，而不是像批量归一化那样依赖于批次大小。这使得它不受批次大小的影响，尤其适合批次大小较小的情况。

公式：

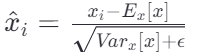
其中，和分别表示该层所有神经元输出的均值和方差。

应用场景：
特别适用于循环神经网络（RNNs）、长短期记忆网络（LSTMs）等序列模型，因为这些模型通常需要处理变长序列，而且对批次大小敏感。

3. 组归一化（Group Normalization）

定义与原理：
组归一化是一种介于批量归一化和层归一化之间的方法，它将通道划分为若干组，并在每个小组内执行归一化。这种方法旨在结合批量归一化的高效性和层归一化的鲁棒性。

应用场景：
非常适合在批次大小较小或不固定的情况下使用，如在图像分割、目标检测等任务中，尤其是在批次大小较小时，能提供比批量归一化更稳定的训练过程。

4. 实例归一化（Instance Normalization）

定义与原理：
实例归一化类似于组归一化，但它只考虑每个样本的每个通道独立地进行归一化，而不跨通道计算统计量。主要用于风格迁移等任务中。

应用场景：
主要用于生成对抗网络（GANs）和风格迁移等任务，在这些场景下，每个图像的样式信息是非常重要的，而实例归一化能够有效地捕捉这种样式信息。

总结

批量归一化 是最常用的归一化方法之一，但它的效果依赖于批次大小。
层归一化 不依赖于批次大小，因此更适合用于RNNs和LSTMs等序列模型。
组归一化 提供了一种灵活的方法来平衡批量归一化和层归一化的优势，特别是在批次大小较小时表现良好。
实例归一化 特别适用于风格迁移等任务，因为它能够有效捕捉并保留每个图像的样式信息。
每种归一化方法都有其适用场景和优势，选择合适的归一化策略取决于具体的应用背景和需求。

场景二：音频信号处理

音频幅度通常被归一化到 [-1, 1]，这样便于数字信号处理和避免溢出。

场景三：游戏开发中的坐标标准化

在 3D 游戏引擎中，顶点坐标有时会被归一化到 [-1, 1] 的视口空间，便于渲染。

总结

不同的归一化方法适用于不同类型的数据集和应用场景。例如，如果数据分布接近正态分布，Z-Score标准化可能是更好的选择；而对于有明确上下界的数值，如图像像素值，最小-最大归一化可能更合适。

这些方法都有助于提高模型的性能，减少某些算法对输入规模敏感的问题。在实际应用中，选择合适的归一化方法需要根据具体的数据特征和业务需求来决定。