自注意力机制（Self-Attention）

概述

普通自注意力（Self-Attention）的工作原理主要是让模型能够关注输入序列中不同位置的信息，并根据这些信息来生成当前位置的输出。它是Transformer模型中的一个关键组件，尤其在处理序列数据（如文本、语音等）时表现出色。

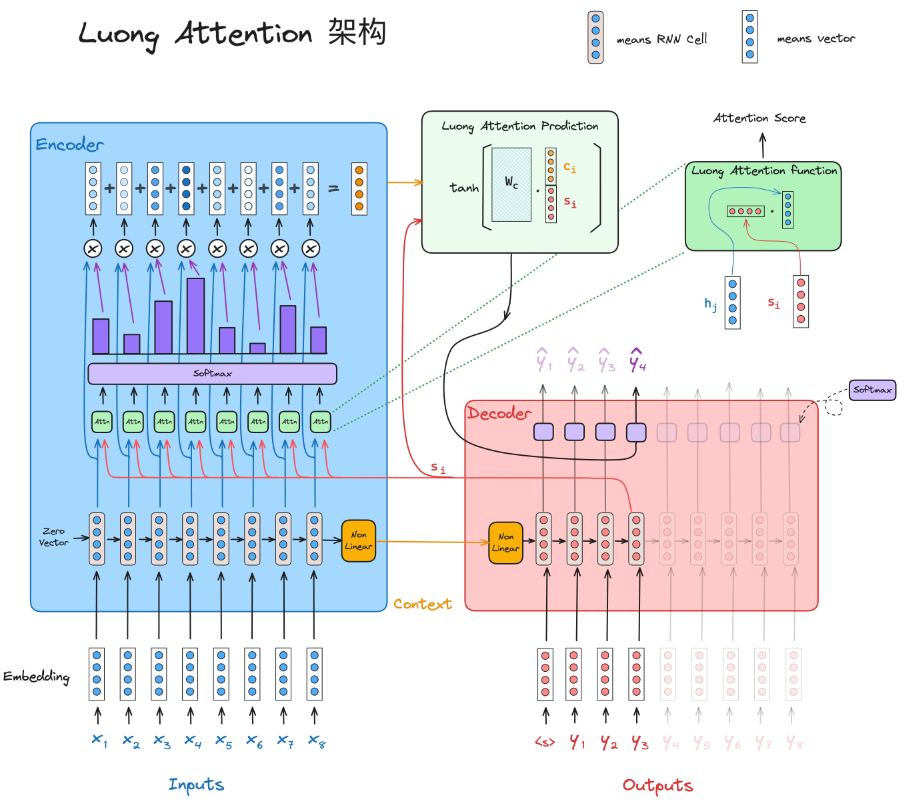
以下是自注意力机制的优缺点分析：

优点：

能够捕获长距离依赖：自注意力机制允许模型在计算序列中某个位置的表示时，直接参考整个序列的其他位置，从而能够捕获长距离的依赖关系。这在处理长序列时尤为重要，因为它不受传统RNN中逐步传递信息的限制。
并行计算：自注意力机制在计算时不需要按照序列的顺序逐步进行，因此可以并行地处理序列中的所有位置，大大提高了计算效率。
动态权重：自注意力机制为每个输入位置生成不同的权重，这些权重是动态计算的，基于输入序列的当前内容。这使得模型能够自适应地关注重要的输入部分，从而提高模型的表示能力。
可解释性：自注意力机制中的注意力权重可以为模型提供一定程度的可解释性。通过分析这些权重，我们可以了解模型在做出决策时关注了哪些输入部分，从而有助于理解模型的内部工作原理。

缺点：

计算复杂度：自注意力机制的计算复杂度与序列长度的平方成正比。这意味着在处理长序列时，自注意力机制的计算成本会显著增加，可能导致训练速度变慢或需要更多的计算资源。
空间复杂度：自注意力机制需要存储序列中所有位置之间的相关性得分，这会导致较高的空间复杂度。在处理长序列时，这可能会成为问题，因为需要消耗大量的内存或显存资源。
缺乏位置信息：自注意力机制在计算时并不直接考虑序列中单词的位置信息。这可能导致模型在处理需要位置信息的任务时表现不佳。为了解决这个问题，通常会在输入序列中添加位置编码（如正弦和余弦函数的位置编码）来提供位置信息。
模型复杂性：自注意力机制本身的结构相对复杂，需要更多的参数和计算资源。这可能会增加模型的训练难度和过拟合风险。
对于特定任务的限制：尽管自注意力机制在自然语言处理任务中取得了显著的成功，但它可能并不适用于所有类型的任务。在某些情况下，更简单的模型结构可能更为有效。

计算过程

下面我将使用一个简单的例子来一步步演示自注意力机制的计算过程。

假设

假设我们有一个简单的输入序列，该序列包含4个单词（或标记），表示为 [w1, w2, w3, w4]。为了简化，我们假设每个单词的嵌入向量都是2维的。

步骤

1. 输入嵌入（Input Embedding）

首先，将输入的序列数据（如文本序列）转换为嵌入向量（embedding vectors）表示。对于文本数据，这通常是通过一个词嵌入矩阵（word embedding matrix）来实现的，该矩阵将每个单词映射到一个高维的向量空间。

假设嵌入后的向量如下（这里只是示例值）：

w1 = [1, 0]  
w2 = [0, 1]  
w3 = [1, 1]  
w4 = [0, 0]

2. 位置编码（Positional Encoding）（简化示例中省略）

在实际应用中，我们需要添加位置编码，但在此示例中为了简化，我们省略这一步骤。

3. 查询（Query）、键（Key）和值（Value）的计算

对于序列中的每个位置，使用三个不同的线性变换（即三个不同的权重矩阵）来生成查询（Q）、键（K）和值（V）向量。这些变换通常是全连接层（或称为线性层）实现的，可以将嵌入向量（或嵌入向量与位置编码的和）转换为不同的维度空间。
对于输入序列中的每个位置 (i)，通过线性变换得到查询（Query）、键（Key）和值（Value）的向量表示：

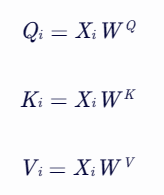其中，(X_i) 是输入序列中第 (i) 个位置的嵌入向量（或包含位置编码的嵌入向量），(W^Q), (W^K), (W^V) 是可学习的权重矩阵。

这里我们假设线性变换的权重矩阵是固定的，并使用相同的权重矩阵来生成Q、K和V（在实际情况中，Q、K和V通常有不同的权重矩阵）。

假设权重矩阵 W_q = W_k = W_v = [[1, 0], [0, 1]]（同样，这只是一个示例），则：

Q1 = W_q * w1 = [1, 0]  
Q2 = W_q * w2 = [0, 1]  
Q3 = W_q * w3 = [1, 1]  
Q4 = W_q * w4 = [0, 0]  
  
K1 = W_k * w1 = [1, 0]  
K2 = W_k * w2 = [0, 1]  
K3 = W_k * w3 = [1, 1]  
K4 = W_k * w4 = [0, 0]  
  
V1 = W_v * w1 = [1, 0]  
V2 = W_v * w2 = [0, 1]  
V3 = W_v * w3 = [1, 1]  
V4 = W_v * w4 = [0, 0]

（注意：在实际应用中，Q、K和V通常具有不同的维度，但在这里为了简化，我们假设它们与嵌入向量的维度相同。）

4. 计算注意力分数（Attention Scores）

对于每个位置 (i)，计算其查询向量 (Q_i) 与所有位置 (j) 的键向量 (K_j) 的点积（dot product），并除以一个缩放因子 (\sqrt{d_k})（(d_k) 是键向量的维度，用于防止梯度消失），得到注意力得分。这些得分表示了当前位置与其他位置之间的相关性：

使用点积来计算注意力分数，并除以 (\sqrt{d_k})（在这里 (d_k = 2)）：

Score(Q1, K1) = Q1 · K1 / sqrt(2) = 1  
Score(Q1, K2) = Q1 · K2 / sqrt(2) = 0  
Score(Q1, K3) = Q1 · K3 / sqrt(2) = 0.707  
Score(Q1, K4) = Q1 · K4 / sqrt(2) = 0  
... (类似地计算其他Q和K的点积)

5. 应用softmax函数

将注意力得分输入到softmax函数中，得到注意力权重。softmax函数将原始得分转换为概率分布，使得所有位置的注意力权重之和为1。

其中，(n) 是序列的长度。

下面简化计算，将注意力分数转换为注意力权重：

Weight(Q1, K1) = softmax([1, 0, 0.707, 0]) = ... (具体值取决于softmax函数)  
... (类似地计算其他权重)

6. 加权求和

使用注意力权重对值向量进行加权求和，得到每个位置的输出表示。这个过程也被称为上下文向量（Context Vector）的计算，因为它包含了整个序列的上下文信息。

使用注意力权重对值向量进行加权求和：

Output1 = Weight(Q1, K1) * V1 + Weight(Q1, K2) * V2 + ...  
... (类似地计算其他位置的输出)

7. 多头自注意力（Multi-Head Self-Attention）（简化示例中省略）

在实际应用中，会并行进行多个“头”的自注意力计算，并将结果拼接起来。但在此示例中，我们省略了这一步骤。

8. 残差连接和层归一化（Residual Connection and Layer Normalization）（简化示例中省略）

在实际应用中，还会将自注意力层的输出与原始输入相加，并进行层归一化。但在此示例中，我们省略了这一步骤。

9. 前馈神经网络（Feed-Forward Neural Network）（简化示例中省略）

最后，还会将自注意力层的输出传递给一个前馈神经网络进行进一步处理。但在此示例中，我们省略了这一步骤。

余弦相似度（Cosine Similarity）

修正余弦相似度（Adjusted Cosine Similarity）

皮尔逊χ²检验（Pearson's Chi-squared Test）

互信息（Mutual Information, MI）

Tanimoto系数（Tanimoto Coefficient）

切比雪夫距离（Chebyshev Distance）

汉明距离（Hamming Distance）

朴素贝叶斯分类算法（Naive Bayes Classification Algorithm

posted @ 2024-06-03 14:05 JackYang 阅读(2578) 评论(0) 收藏举报

刷新页面返回顶部