Java中的梯度下降-Java快速进阶教程

1. 简介

在本教程中，我们将了解梯度下降算法。我们将在 Java 中实现该算法并逐步说明它。

2. 什么是梯度下降？

梯度下降是一种优化算法，用于查找给定函数的局部最小值。它广泛用于高级机器学习算法中，以最小化损失函数。

坡度是坡度的另一个词，下降意味着下降。顾名思义，梯度下降沿着函数的斜率向下，直到它到达终点。

3. 梯度下降的性质

梯度下降查找局部最小值，该最小值可能与全局最小值不同。起始局部点作为算法的参数给出。

这是一个迭代算法，在每一步中，它都试图沿着斜率向下移动并接近局部最小值。

在实践中，该算法是回溯的。我们将在本教程中说明和实现回溯梯度下降。

4. 分步说明

梯度下降需要一个函数和一个起点作为输入。让我们定义并绘制一个函数：

我们可以从任何想要的点开始。让我们从x=1 开始：

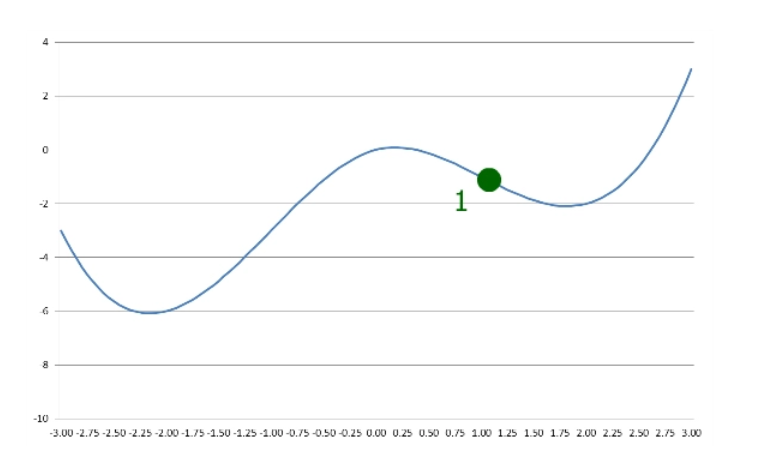
在第一步中，梯度下降以预定义的步长沿着斜坡向下：

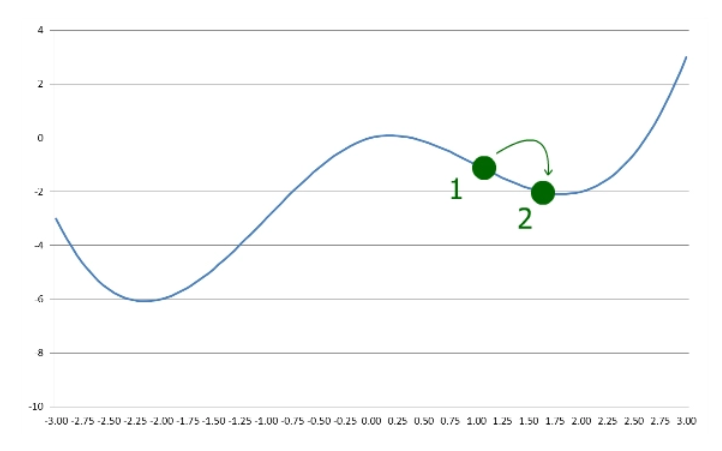
接下来，它以相同的步长走得更远。但是，这次它最终比最后一步的y大：

 

这表示算法已超过局部最小值，因此它以减小的步长向后移动：

 

 

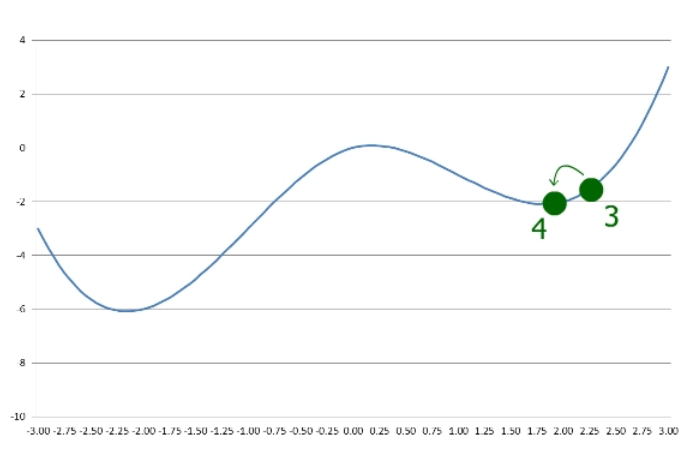
随后，每当当前 y 大于前一个y 时，步长就会降低并取反。迭代继续进行，直到达到所需的精度。

正如我们所看到的，梯度下降在这里发现了一个局部最小值，但它不是全局最小值。如果我们从 x=-1 而不是x=1 开始，将找到全局最小值。

5. 在 Java 中的实现

有几种方法可以实现梯度下降。在这里，我们不计算函数的导数来找到斜率的方向，因此我们的实现也适用于不可微函数。

让我们定义精度和步进系数，并给出它们的初始值：

 

double precision = 0.000001;
double stepCoefficient = 0.1;Copy

第一步，我们没有用于比较的前y。我们可以增加或减少x的值，看看y是降低还是提高。正步进系数意味着我们正在增加x 的值。

现在让我们执行第一步：

double previousX = initialX;
double previousY = f.apply(previousX);
currentX += stepCoefficient * previousY;Copy

在上面的代码中，f是一个Function<Double、Double>，initialX是一个double，两者都作为输入提供。

另一个需要考虑的关键点是梯度下降不能保证收敛。为了避免陷入循环，让我们对迭代次数进行限制：

int iter = 100;Copy

稍后，我们将在每次迭代时将iter 递减 1。因此，我们将在最多 100 次迭代时退出循环。

现在我们有一个previousX，我们可以设置我们的循环：

while (previousStep > precision && iter > 0) {
    iter--;
    double currentY = f.apply(currentX);
    if (currentY > previousY) {
        stepCoefficient = -stepCoefficient/2;
    }
    previousX = currentX;
    currentX += stepCoefficient * previousY;
    previousY = currentY;
    previousStep = StrictMath.abs(currentX - previousX);
}Copy

在每次迭代中，我们计算新的y 并将其与之前的y 进行比较。如果currentY大于previousY，我们改变方向并减小步长。

循环一直持续到我们的步长小于所需的精度。最后，我们可以返回currentX作为局部最小值：

return currentX;