2025.8.16学习日记

三维空间的刚体运动

旋转矩阵

坐标系之间的欧式变换

这一部分的前提假设是，对于同一向量p，在不同坐标系中，有不同的表示。通过等式p=(e1,e2,e3)(a1,a2,a3)T=(e1',e2',e3')(a1',a2',a3')T找到不同坐标系之间同一个点的表示，最后表示为如下：

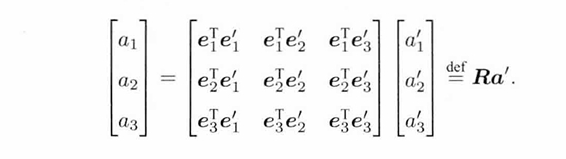
【注】：矩阵R有两组基互相做内积得到，向量和它的加减法，内外积这些运算不用通过坐标系也能够得到。例如在有坐标时，内积可以通过分量乘积之和得到，在没有坐标时，也可以通过长度和夹角计算得到。所以说内积结果与坐标选择无关

从坐标系的欧式变换应用到向量的旋转变换

根据旋转矩阵的定义:行列式为1的正交矩阵,可以验证这个欧式变换确实是一个旋转变换R,可以通过如下公式计算其夹角和旋转轴

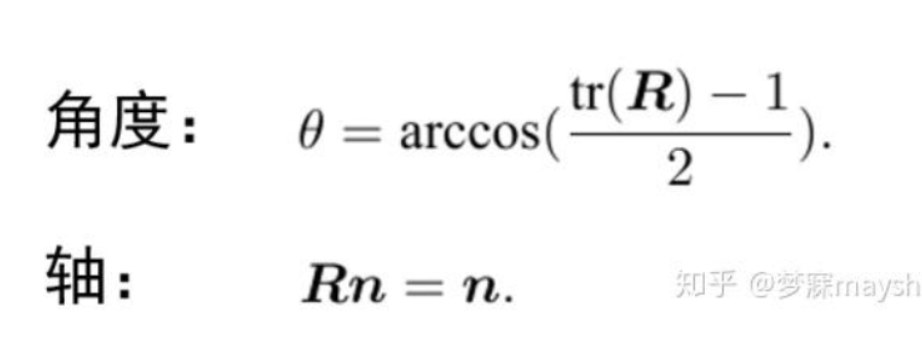
【注】：这里有一种主被动的理解方式，待旋转点主动转θ后得到的坐标，等于待旋转点不动，坐标系转动-θ得到的坐标；缩短两人之间的距离，要么一个人前进x米，要么另一个人后退x米

约定写法

其中R12需要从右向左读取，表示为某一向量从坐标系2到坐标系1内的坐标。t12需要从左向右读取，表示为坐标1的原点指向坐标系2的原点，在坐标系1下的表示

旋转向量和欧拉角

为了减少约束，并且更加紧凑地表示旋转矩阵，引入了旋转向量这一概念，旋转向量的方向与转轴一致，旋转向量的长度等于旋转角；同样地为了更加紧凑地表示变换矩阵，使用一个旋转向量和一个平移向量就可以表示一个变换矩阵

旋转向量和旋转矩阵的转换

现在考虑一个旋转矩阵R，假设旋转轴为单位向量n，旋转角度为α，那么向量αn就通过罗德利斯公式转换为旋转矩阵，来表示这个旋转

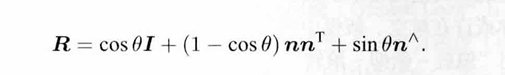
欧拉角

无论是旋转矩阵，还是旋转向量，虽然能描述旋转，单对于人来说是非常不直观的；即使用这两个东西更像是在代数上使用，难以在几何中想象出旋转究竟是什么；使用欧拉角就可以，但是欧拉角具有奇异性，万向锁，

四元数

四元数和旋转向量一样是紧凑的，同时比起旋转向量来说不带有奇异性；它是紧凑的，也没有奇异性

加减法

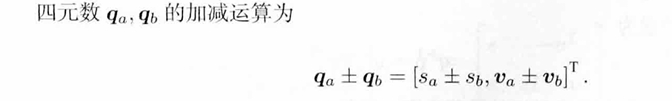
乘法

四元数与旋转向量之间的转换