2025.8.15学习日记

BA优化

BA全称为bundle_adjustment,现在复习一些前置概念

左手系和右手系

关键在于你想让Z轴指向内部还是指向外部，如果Z轴指向内部，并采用右手系，那么左侧为x正半轴，上侧为y为正半轴(或者右侧为x正半轴，下侧为y轴正半轴)

外参矩阵-内参矩阵-投影矩阵

由旋转矩阵R和平移向量T组成的4阶矩阵称为外参矩阵记为[R|T],将相机视图投影到归一化空间的矩阵称为内参矩阵记为K;现在将原空间(世界空间)到归一化空间的矩阵记为P=K[R|T]

BA算法的表达式

原图的连接在这里,这里解释一下,gi表示每个相机的外参也就是世界->相机,gij表示相机i到相机j的相对变换,如何理解这个gi逆与gj这两个矩阵的乘积呢,可以从传递性的角度来理解,传递性是离散数学中对于等价关系的定义的一个必要条件,由gi的定义可以知道,gi是世界(也可以假设成一个不存在的相机0)->相机i,那么gi逆就是相机i->世界,靠传递关系来理解的话就是相机i->世界,然后再是世界->相机j,这样就得到了相机i->相机j

那么从之里就可以理解处BA优化问题的优化目标就是找到一组全局的相机外参{g1,g2,...gN},使得与观测到的相对相机外参{gij}的误差最小

BA算法的实践

BA优化首先初始化旋转矩阵,在初始化旋转矩阵时,用到了李代数空间和普通三维空间组合而成的一个6维空间;

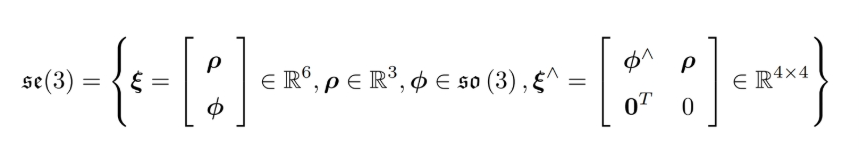
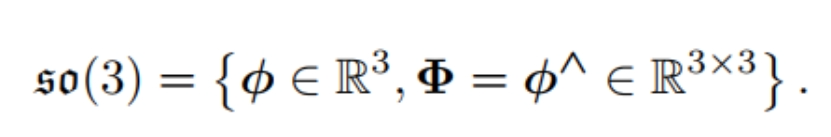
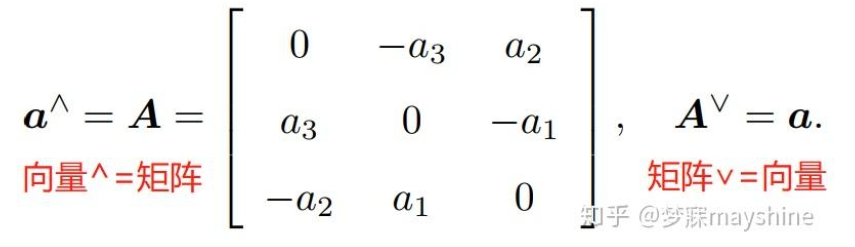
而后通过一个指数映射,将李代数ξ对应的矩阵ξ^变为变换矩阵T

【注1】：python一般将空字符串作为当前工作目录，例如在sys.path中一般使用''空字符串表示当前工作目录,这样python就能从sys.path获得绝对导入import的路径
【注2】：如果想将其从R这一旋转矩阵中解耦出旋转角度和旋转轴，以及从ρ中解耦出t需要用到如下公式

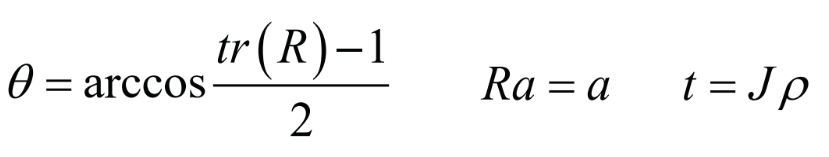
辅助理解的概念

SE3

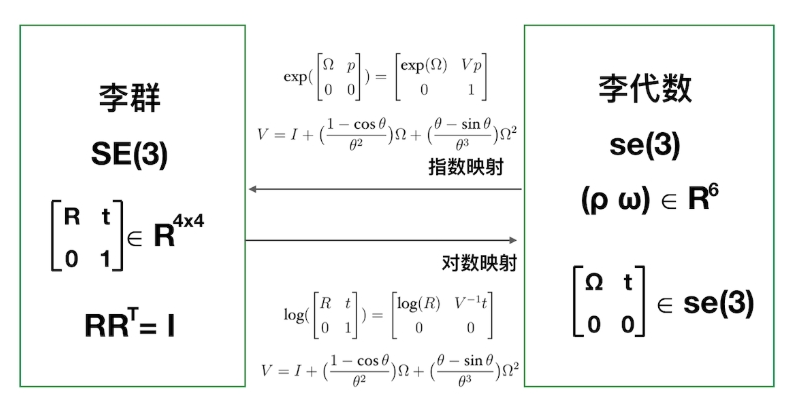
SO3

罗德利斯公式

向量形式
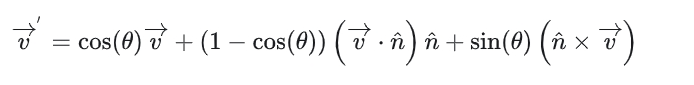
矩阵形式

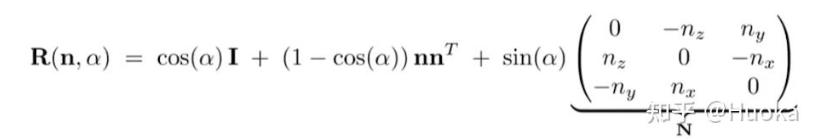
【注1】：v'=R(n,a)v,可以将旋转矩阵联想记为RNA，即核糖核酸
【注2】：第二项根据数与向量的交换律,可以先将n拿到内积(v,n)之前,根据内积之间对称性(v,n)=(n,v),以及矩阵乘法与内积的对应,可以将(n,v)写成nTv,再根据结合律,可以先算nnT
【注3】：第三项根据在3维空间内,外积(也叫叉乘)的本质,实际上是求解一个Rank=2的齐次线性方程组,我们可以知道实际上只要求满足nTx=0且vTx=0的x即可,现在将x替换为Nv,带入原来的方程可以获得nTNv=0,与vTNv=0的表达式,从第二条表达式来看,其实就是一元二次方程,从第一条表达式来看,式二元二次方程,由待定系数可以知道二次项的系数都应该为0,对应矩阵N即对角线的元素都为0,而且一次项的系数也为0,那么可以知道,主对角线上的元素加起来应该相互抵消,此时为了N的形式更为美观,规定其为反对称矩阵,主对角线为0,且副对角线为相反数.至于排列顺序涉及到外积向量的方向,在这里不深究
【注4】：更好的解释