fmatmul浮点矩阵乘的risc-v向量指令实现

背景

矩阵乘法是众多科学计算和人工智能应用中的核心计算部分。同样，在高性能计算领域，许多线性代数算法也都依赖于高效的矩阵乘法实现。因此，矩阵乘法的性能优化成为了提升整个计算系统性能的重要途径。

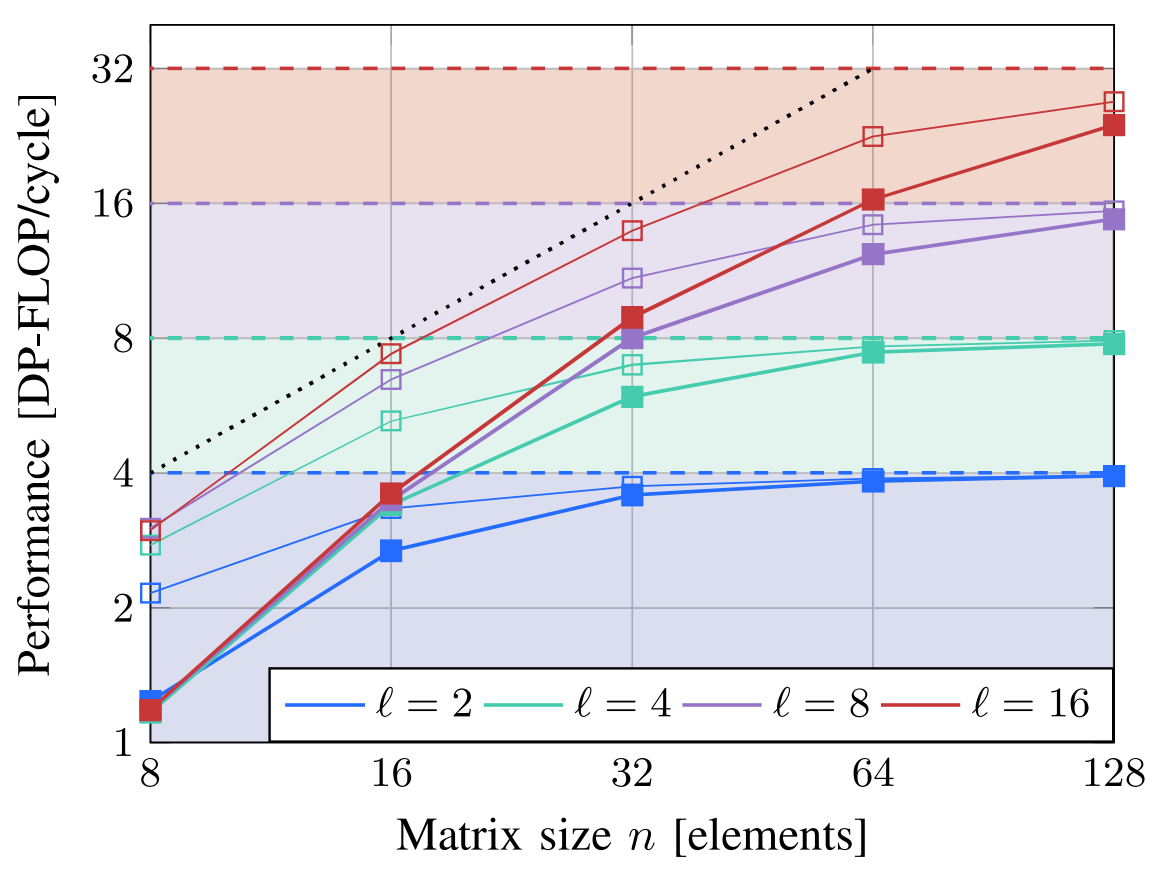
在评估处理器性能尤其是向量扩展时，矩阵乘法常常作为一个典型的测试用例。在进行RTL仿真或物理机测试时，通过运行矩阵乘法可以测量处理器的动态指令数和运行周期数等性能指标。如下图所示，在ARA处理器中，通过Roofline模型展示了不同大小的矩阵乘法和不同lane数下的利用率。

在处理器架构中，向量指令集扩展（Vector Extension）作为一种重要的技术手段，通过并行化处理数据来提升计算性能。向量指令集允许单条指令操作多个数据（SIMD），从而减少循环次数和动态指令数，并通过增加运算单元来提高数据处理速度。因此，如何用向量指令高效实现矩阵乘法成为评估硬件性能的基础。

这篇文章将学习如何利用向量指令来实现高效的矩阵乘法。通过算法分析和代码分析，分析如何在向量扩展处理器上进行矩阵乘法优化的具体方法和效果。有助于理解向量指令集的实际应用，还能为处理器性能优化提供参考。

矩阵乘的向量化

参考 goto矩阵乘 https://www.twisted-meadows.com/high-performance-gemm/

考虑到存储体系，先对矩阵进行分块，然后对于分块的矩阵采用Rank-1 Update的方法，用A分块矩阵的列向量乘以B分块矩阵的行向量进行累加得到C分块矩阵

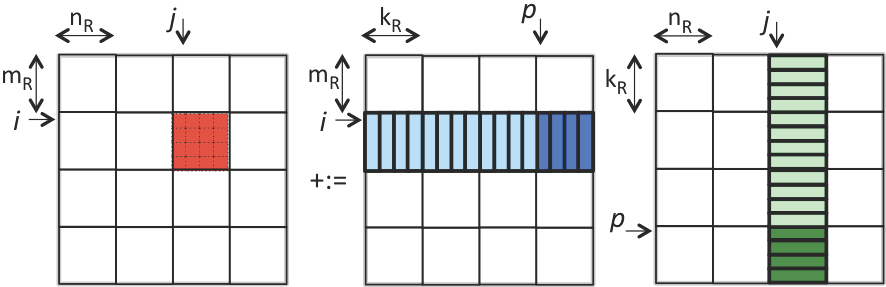
其中A分块矩阵的列向量可以再细分为元素，这样就变成了向量乘累加

ara中的fmatmul

fmatmul中会根据矩阵尺寸调用不同分块大小的矩阵乘函数

void fmatmul(double *c, const double *a, const double *b,
             const unsigned long int M, const unsigned long int N,
             const unsigned long int P) {
  if (M <= 4) {
    fmatmul_4x4(c, a, b, M, N, P);
  } else if (M <= 8) {
    fmatmul_8x8(c, a, b, M, N, P);
  } else if (M <= 64) {
    fmatmul_16x16(c, a, b, M, N, P);
  } else if (M <= 128) {
    // Vector length is 64 elements. With an 8x8 matmul,
    // we can use LMUL=2, having a vl of 128.
    fmatmul_8x8(c, a, b, M, N, P);
  } else {
    // Vector length is 64 elements. With an 4x4 matmul,
    // we can use LMUL=4, having a vl of 256.
    fmatmul_4x4(c, a, b, M, N, P);
  }
}

以fmatmul_16x16为例

void fmatmul_16x16(double *c, const double *a, const double *b,
                   unsigned long int M, unsigned long int N,
                   unsigned long int P) {
  // We work on 4 rows of the matrix at once
  const unsigned long int block_size = 16;
  unsigned long int block_size_p;

  // Set the vector configuration
  asm volatile("vsetvli %0, %1, e64, m1, ta, ma" : "=r"(block_size_p) : "r"(P));

  // Slice the matrix into a manageable number of columns p_
  for (unsigned long int p = 0; p < P; p += block_size_p) {
    // Set the vector length
    const unsigned long int p_ = MIN(P - p, block_size_p);

    // Find pointers to the submatrices
    const double *b_ = b + p;
    double *c_ = c + p;

    asm volatile("vsetvli zero, %0, e64, m1, ta, ma" ::"r"(p_));

    // Iterate over the rows
    for (unsigned long int m = 0; m < M; m += block_size) {
      // Find pointer to the submatrices
      const double *a_ = a + m * N;
      double *c__ = c_ + m * P;

      fmatmul_vec_16x16_slice_init();
      fmatmul_vec_16x16(c__, a_, b_, N, P);
    }
  }
}

对于每个分块矩阵，使用向量乘累加来获得

void fmatmul_vec_16x16(double *c, const double *a, const double *b,
                       const unsigned long int N, const unsigned long int P) {
  // Temporary variables
  double t0, t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12, t13, t14, t15;

  // Original pointer
  const double *a_ = a;

  // Prefetch one row of scalar values
  t0 = *a, a += N;
  t1 = *a, a += N;
  .
  .
  .
  t15 = *a;

  // Prefetch one row of matrix B
  asm volatile("vle64.v v16, (%0);" ::"r"(b));
  b += P;

  // Compute the multiplication
  unsigned long int n = 0;

  while (n != N) {
#ifdef VCD_DUMP
    // Start dumping VCD
    if (n == 8)
      event_trigger = +1;
    // Stop dumping VCD
    if (n == 12)
      event_trigger = -1;
#endif

    // Calculate pointer to the matrix A
    a = a_ + ++n;

    asm volatile("vfmacc.vf v0, %0, v16" ::"f"(t0));
    t0 = *a, a += N;

    // Load one row of B
    asm volatile("vle64.v v17, (%0);" ::"r"(b));
    b += P;

    asm volatile("vfmacc.vf v1, %0, v16" ::"f"(t1));
    t1 = *a, a += N;
    asm volatile("vfmacc.vf v2, %0, v16" ::"f"(t2));
    t2 = *a, a += N;
    .
    .
    .
    asm volatile("vfmacc.vf v14, %0, v16" ::"f"(t14));
    t14 = *a, a += N;
    asm volatile("vfmacc.vf v15, %0, v16" ::"f"(t15));
    t15 = *a;

    a = a_ + ++n;

    if (n == N)
      break;

    asm volatile("vfmacc.vf v0, %0, v17" ::"f"(t0));
    t0 = *a, a += N;

    // Load one row of B
    asm volatile("vle64.v v16, (%0);" ::"r"(b));
    b += P;

    asm volatile("vfmacc.vf v1, %0, v17" ::"f"(t1));
    t1 = *a, a += N;
    asm volatile("vfmacc.vf v2, %0, v17" ::"f"(t2));
    t2 = *a, a += N;
    .
    .
    .
    asm volatile("vfmacc.vf v14, %0, v17" ::"f"(t14));
    t14 = *a, a += N;
    asm volatile("vfmacc.vf v15, %0, v17" ::"f"(t15));
    t15 = *a;
  }

  // Last iteration: store results
  asm volatile("vfmacc.vf v0, %0, v17" ::"f"(t0));
  asm volatile("vse64.v v0, (%0);" ::"r"(c));
  c += P;
  asm volatile("vfmacc.vf v1, %0, v17" ::"f"(t1));
  asm volatile("vse64.v v1, (%0);" ::"r"(c));
  c += P;
  asm volatile("vfmacc.vf v2, %0, v17" ::"f"(t2));
  asm volatile("vse64.v v2, (%0);" ::"r"(c));
  c += P;
  .
  .
  .
  asm volatile("vfmacc.vf v14, %0, v17" ::"f"(t14));
  asm volatile("vse64.v v14, (%0);" ::"r"(c));
  c += P;
  asm volatile("vfmacc.vf v15, %0, v17" ::"f"(t15));
  asm volatile("vse64.v v15, (%0);" ::"r"(c));
}

通过vle64加载B子矩阵的一行，将A子矩阵的一个列向量保存到a0~a15标量寄存器，每个vfmacc得到C子矩阵的一个行向量，经过一波vfmacc后获得C子矩阵的部分矩阵，之后a+1和b+P来计算下一个部分矩阵求和叠加，经过N次叠加得到C矩阵子矩阵。