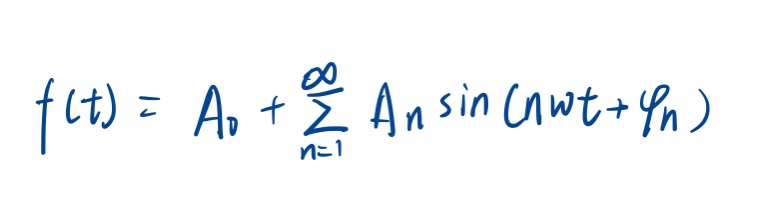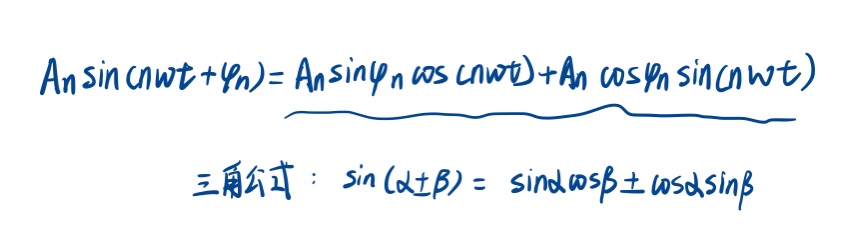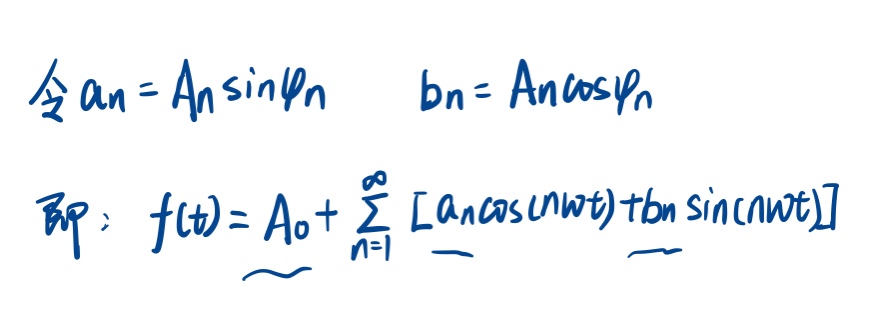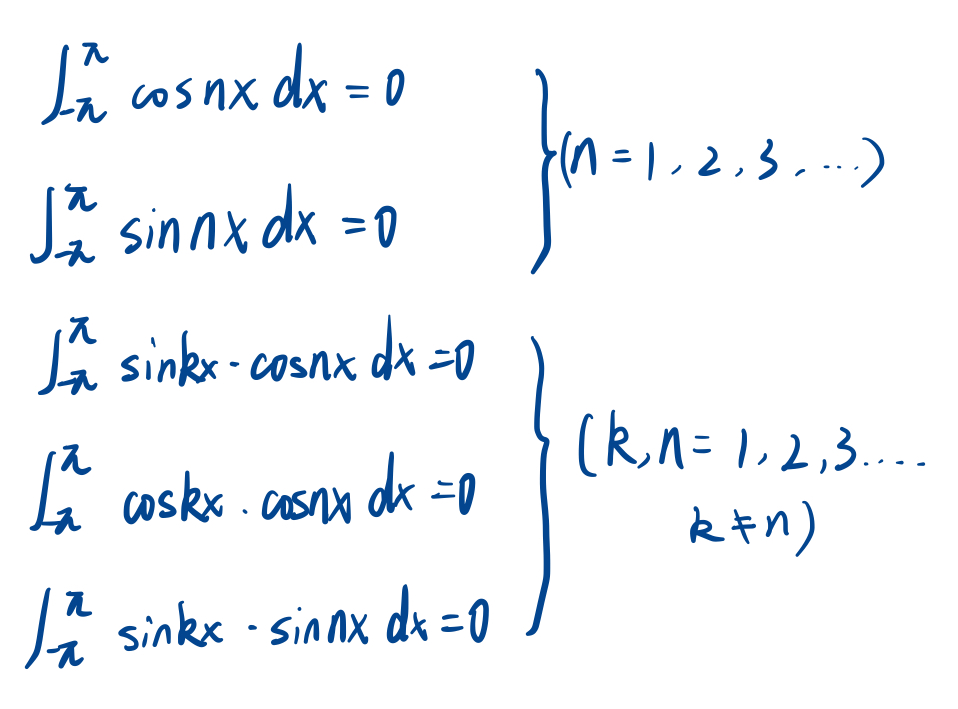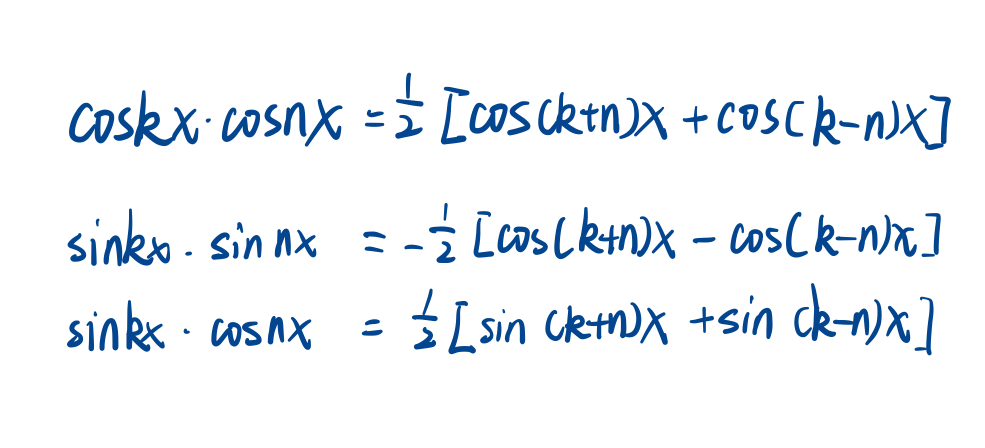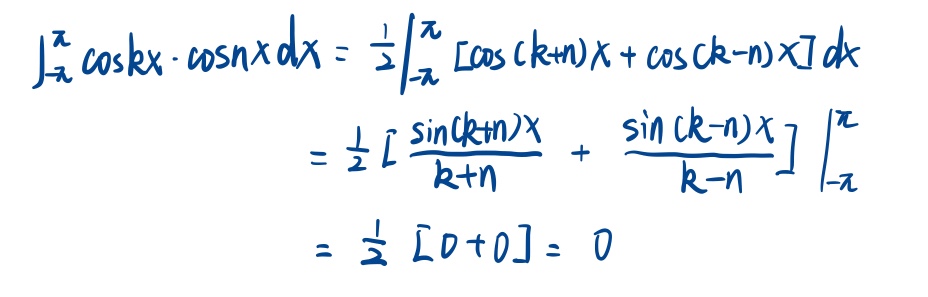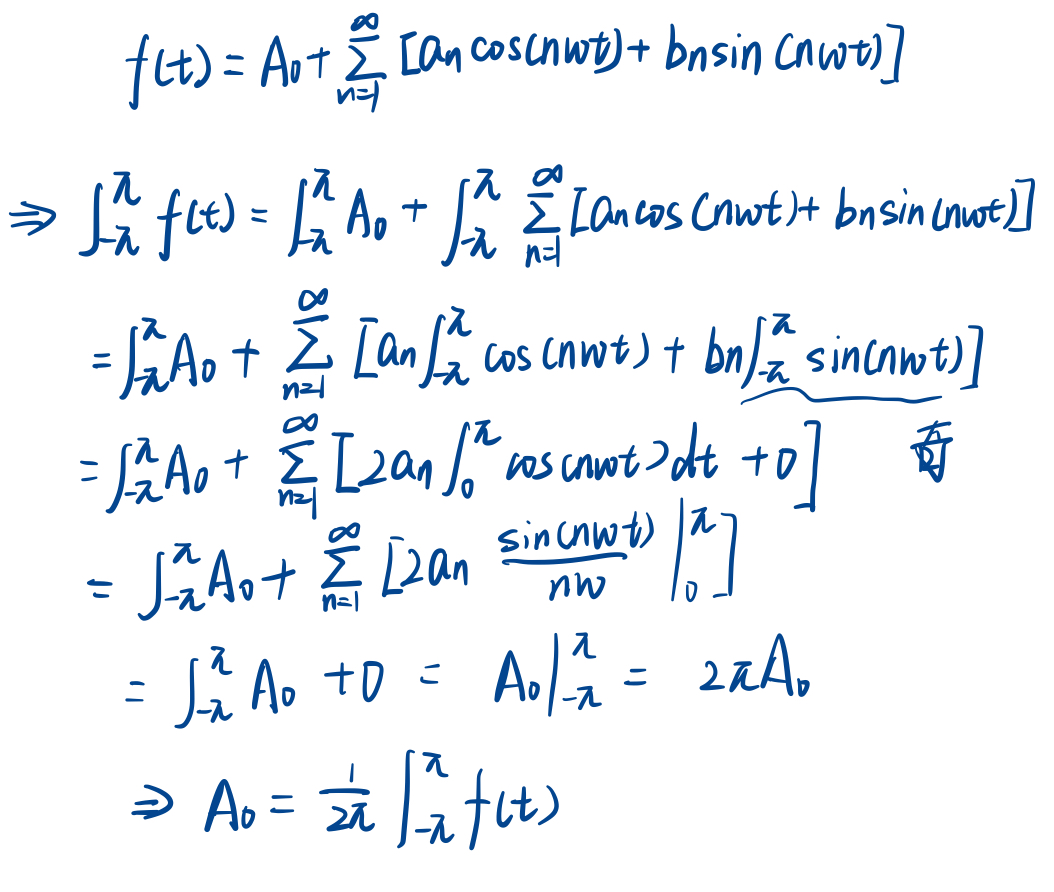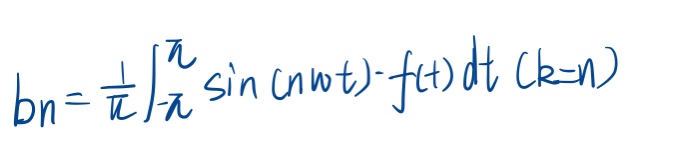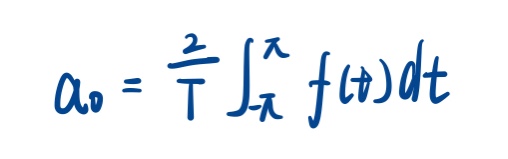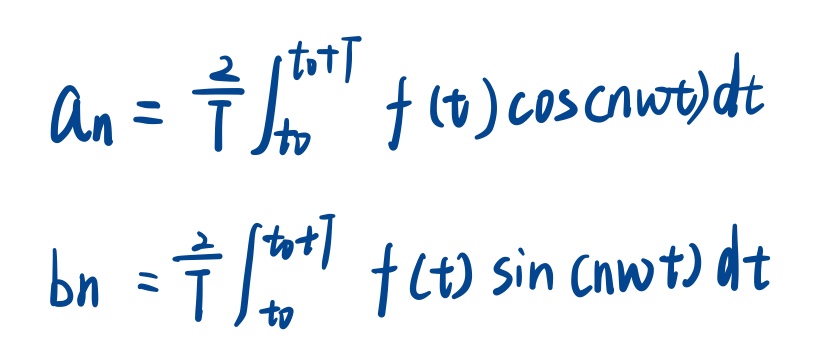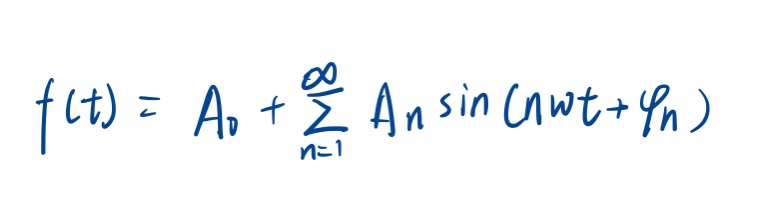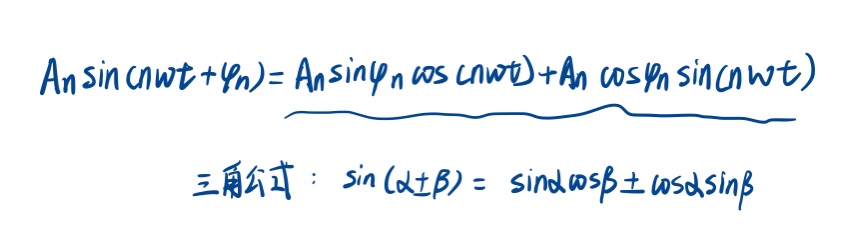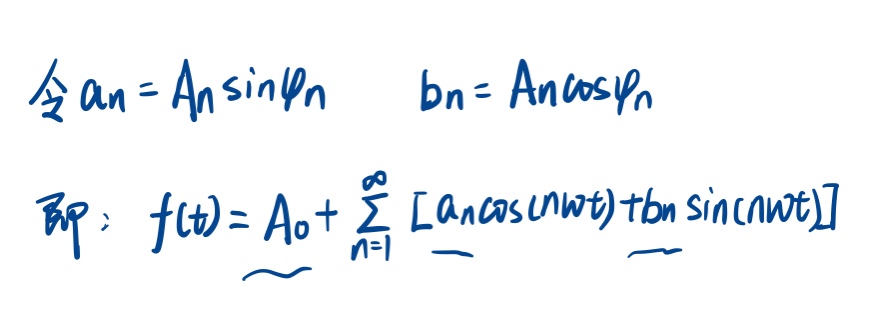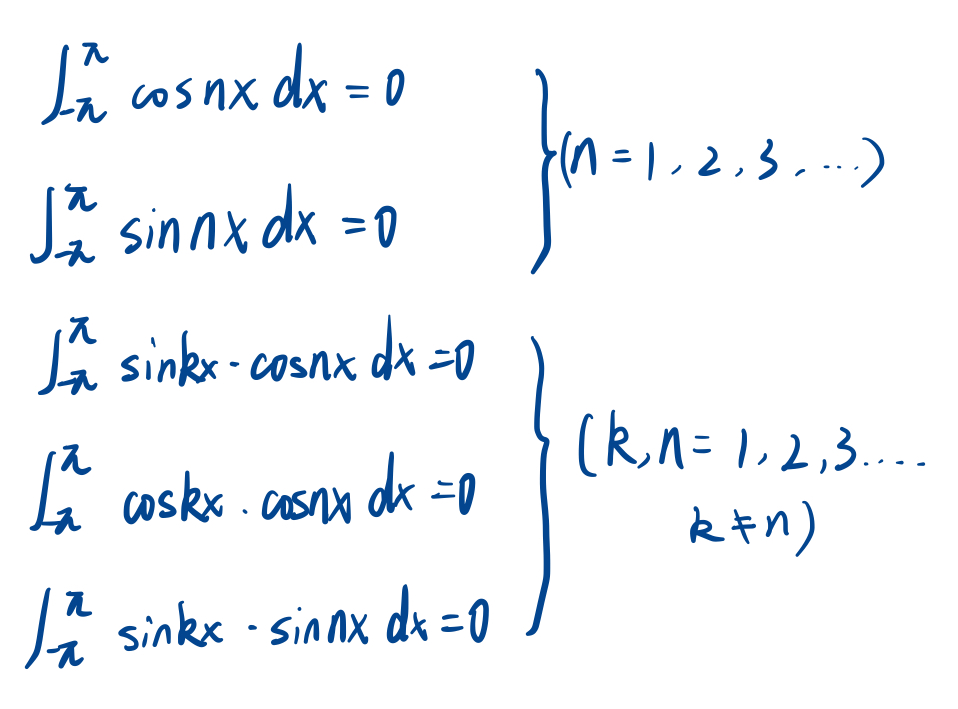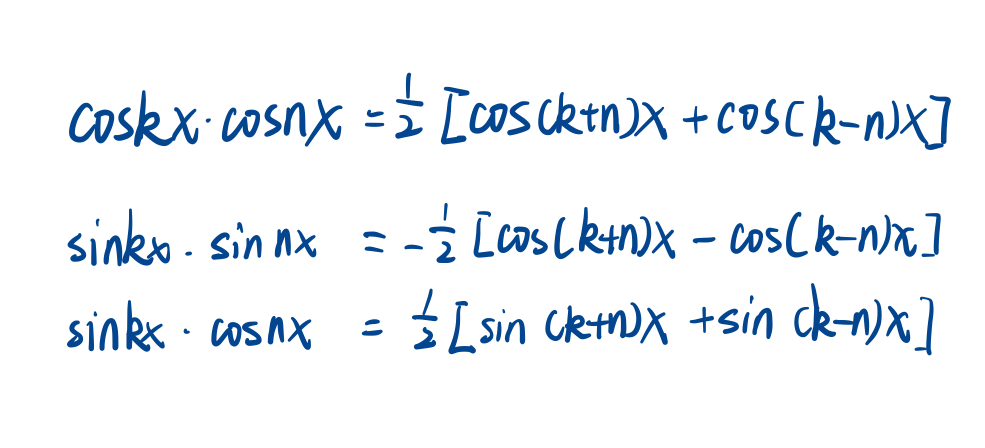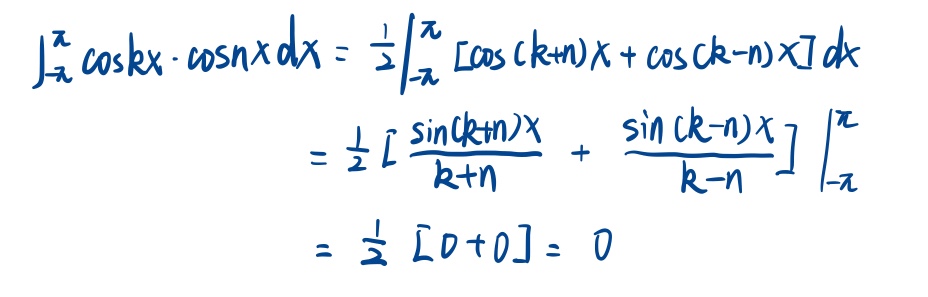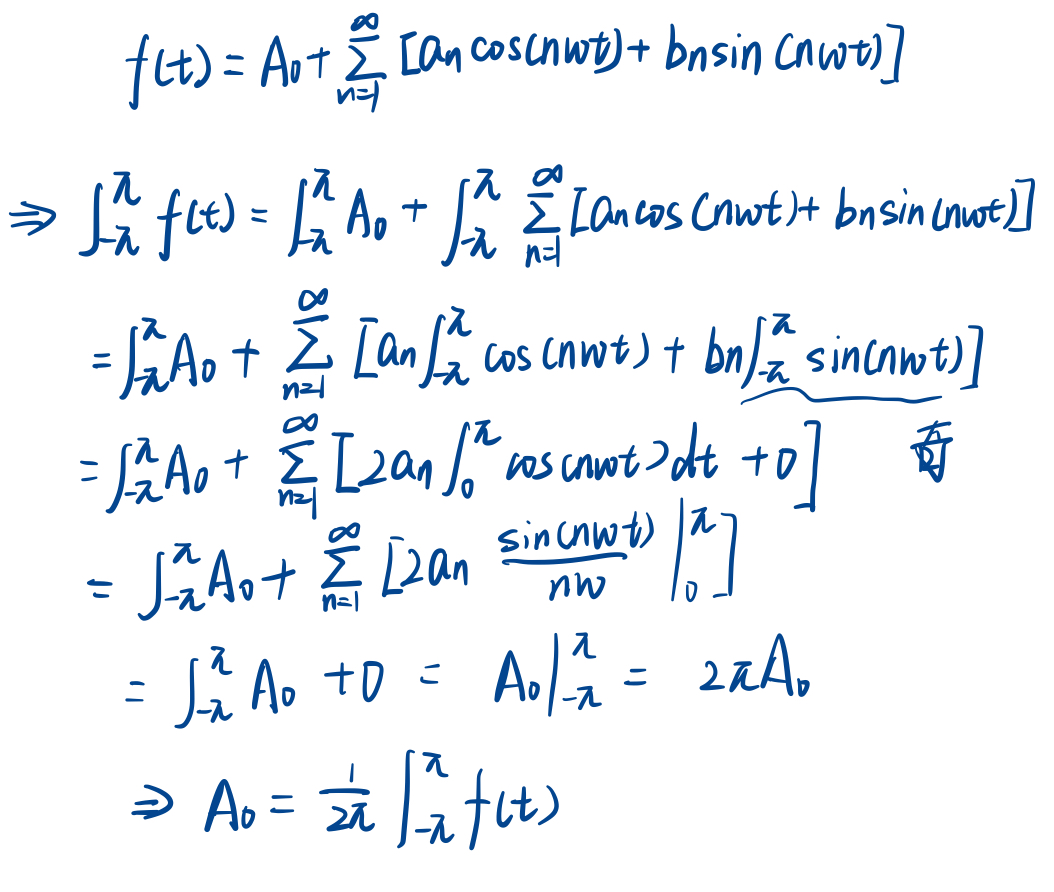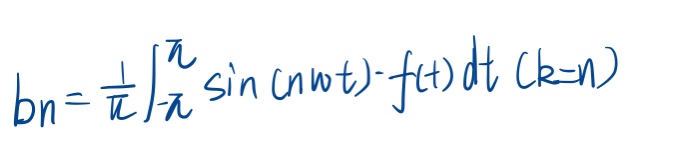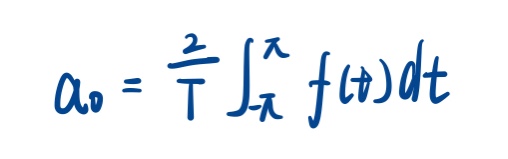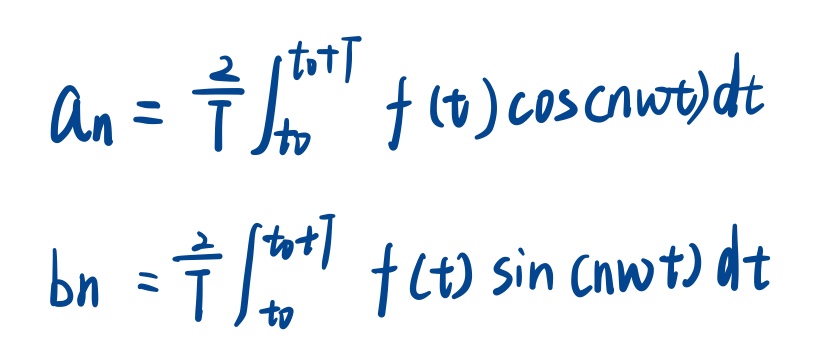傅里叶级数的推导

周期函数是客观世界中周期运动的数学表述，大多可以表示为：
     

然而许多周期信号并非正弦函数那么简单，傅里叶猜想用一系列的三角函数之和来表示那个较复杂的周期函数f(t)，于是就有以下式子：
     

首先先对该式子进行三角函数变形：
     

再把常数项给简化：
     

很明显，我们只需要解出A0，an，bn的值就可以了。
关于三角函数的正交性，有以下式子：
     

注意:第4，5个式子中的k与n不相等，第3个式子的k与n可以相同。后三个式子还可以写成以下形式:
     

当k不等于n时，有：
     

其他式子也可由上面方式同理可以证出。
先把傅里叶级数写成刚才那个式子，并对其从-Π到Π进行积分，可得：
     

目前我们就把A0求出来了
再利用之前那个式子，在他两边同时乘上cos(kwt)，**就可以将an求出来**：
     

同理，两边同时乘上sin(kwt),就可以将bn求出了:
     

因为A0分母为2Π，而an，bn为Π，我们令a0=2A0，就有：
     

变形为：
     

书上的推导的时候假设的T=2Π，代入就得到的以下式子，不影响，随T不同而不同：