平衡树从入门到入土

dly 想要学平衡树，但她打开 oiwiki 后傻眼了。怎么有这么多种平衡树呢？

Treap、FHQ-Treap、Splay、替罪羊、WBLT，甚至还有 01-Trie 实现的平衡树。

各种平衡树有什么不同呢？它们都用什么方法呢？它们的优缺点是什么呢？

如果初学平衡树的你像当初的 dly 那么茫然，那么不妨看一下这篇介绍吧。

二叉搜索树

所有的平衡树都是从二叉搜索树优化而来的。

二叉搜索树，顾名思义，~~首先是一颗二叉树~~。

它的所有点都有一个点权，且一个点左子树里的点的点权都小于它的点权，一个点右子树里的点的点权都大于它的点权。

如下图的这棵树，就是一颗二叉搜索树。

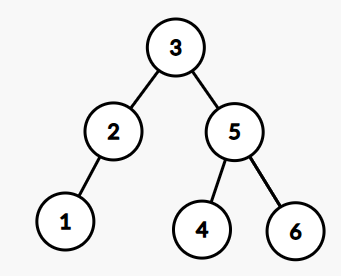
有了上面的性质，我们可以在二叉搜索树上进行很多操作了，如查找第 k 大、查询树中小于某数的数有多少个等。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,rt,tot,a[N],ls[N],rs[N],sz[N];
//ls[u]和rs[u]分别表示u的左右儿子是谁
//a[u]表示u的节点权值
//sz[u]表示u的子树内有多少个数
void insert(int &u,int x)
{
    if(!u){u=++tot,a[u]=x,sz[u]=1;return;}
    if(x<a[u])insert(ls[u],x);
    else if(x>a[u])insert(rs[u],x);
    sz[u]++;
    return;
}
void del(int u,int x)
{
    //这里的del我采用了惰性删除，只改变sz的值，不直接把这个节点从树上删掉
    if(x<a[u])del(ls[u],x);
    else if(x>a[u])del(rs[u],x);
    sz[u]--;
    return;
}
int Rank(int u,int x)//Rank(u,x)表示在u的子树中有几个数比x小
{
    if(!u)return 0;
    else if(x<a[u])return Rank(ls[u],x);
    else if(x>a[u])return sz[u]-sz[rs[u]]+Rank(rs[u],x);
    else return sz[ls[u]];
}
int find(int u,int x)//find(u,x)表示在u的子树中第x大的是哪个数
{
    if(sz[ls[u]]>=x)return find(ls[u],x);
    else if(sz[u]-sz[rs[u]]<x)return find(rs[u],x-sz[u]+sz[rs[u]]);
    else return a[u];
}
int main()
{
    scanf("%d",&n);
    for(int i=1,op,x;i<=n;i++)
    {
        scanf("%d%d",&op,&x);
        if(op==1)insert(rt,x);
        else if(op==2)del(rt,x);
        else if(op==3)printf("%d\n",Rank(rt,x)+1);
        else if(op==4)printf("%d\n",find(rt,x));
        else if(op==5)printf("%d\n",find(rt,Rank(rt,x)));
        else printf("%d\n",find(rt,Rank(rt,x+1)+1));
    }
    return 0;
}

将上面这份代码交到 [P3369 【模板】普通平衡树](P3369 【模板】普通平衡树 - 洛谷) 上，可以获得高达 91 分！

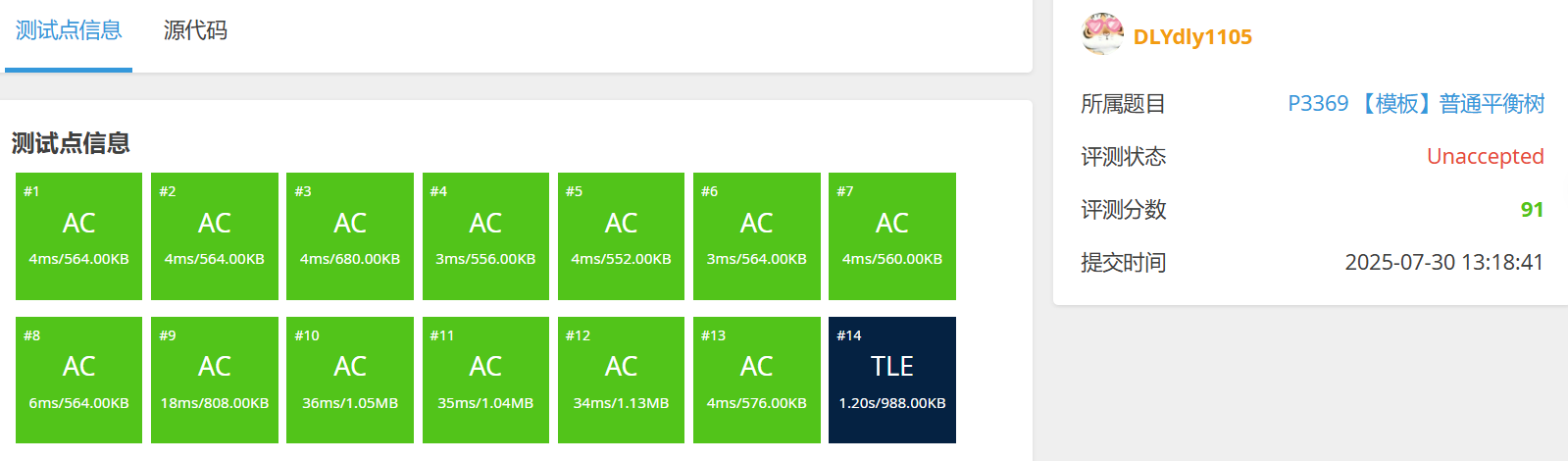
那么，为什么最后一个点会 TLE 呢？

考虑一种情况，我们把要插入的数字从小到大排序后进行插入，那么每次数字会被插到最右边，树一直是一条链。

假设当前树的最大深度是 $x$, 那么函数 insert 的复杂度就是 $O(x)$。

执行 $n$ 次插入操作，总复杂度就是 $O(n^2)$ 的，那么就 TLE 了。

怎么避免这种情况？

这时候就要平衡树出马了，各种平衡树的原理其实都是一样的，即让树高尽可能小，各个节点的左右子树大小尽可能“平衡”（尽可能相等）。

当各个节点的左右子树大小平衡时，显而易见，树高为 $\log n$，那么总复杂度就是 $O(n \log n)$。

替罪羊树

我觉得这应该是最简单、最好写的平衡树了。

我们考虑什么时候树是不平衡的，那么就是左右子树大小相差过大，两者大的那部分占比过多。

于是，我们设定一个阈值 $\alpha$, 这个阈值 $\alpha$ 一般为 $0.7$。设 $sz[u]$ 表示 $u$ 的子树大小，$ch[u][0]$ 和 $ch[u][1]$ 分别表示 $u$ 的左儿子和右儿子（下同），

规定当 $max(sz[ch[u][0]],sz[ch[u][1]])>\alpha \times sz[u]$ 时，判定 $u$ 的子树是失衡的，需要使其平衡。

那么替罪羊树使用什么方法来保持平衡呢？

十分简单粗暴，若 $u$ 的子树失衡了，直接把整棵树推到重构。

比如说下面这棵树，显然 $sz[4]>sz[2]\times 0.7$，那么我们就要对这颗树进行重构了。

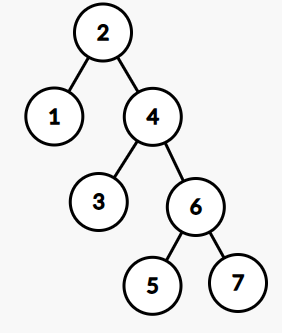
因为二叉搜索树的性质，那么中序遍历得到的序列就是单调递增的，所以我们先进行一遍中序遍历，记录一下每个点的点权，同时在遍历时，让 $sz[u]$ 只保留单点的信息。

然后在重建这棵树，每次取序列的中点为根，那么整棵树就很接近满二叉树了，上图的树经过重构后就会变成下面这样。

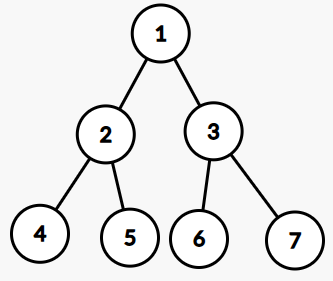
通过上述步骤，我们就可以保证均摊复杂度为 $O(n\log n)$ 了。

完整代码如下。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
const double alpha=0.7;
int n,id,rt,tot,a[N],s[N],sz[N],ch[N][2];
void dfs(int u)
{
    if(ch[u][0])sz[u]-=sz[ch[u][0]],dfs(ch[u][0]);
    s[++tot]=u;
    if(ch[u][1])sz[u]-=sz[ch[u][1]],dfs(ch[u][1]);
    return;
}
void build(int &u,int l,int r)
{
    if(l>r){u=0;return;}//若是l>r说明没有u这个点
    int mid=l+r>>1;
    u=s[mid];//取中点为根
    build(ch[u][0],l,mid-1);
    build(ch[u][1],mid+1,r);
    sz[u]+=sz[ch[u][0]]+sz[ch[u][1]];//重新计算sz
    return;
}
void balance(int &u)
{
    if(max(sz[ch[u][0]],sz[ch[u][1]])<=alpha*sz[u])return;//判断是否失衡
    tot=0,dfs(u),build(u,1,tot);//先dfs中序遍历,然后再暴力重构
    return;
}
//下面这些实际上都和二叉搜索树版本大差不差
void insert(int &u,int x)
{
    if(!u){u=++id,a[u]=x,sz[u]=1;return;}
    if(x<a[u])insert(ch[u][0],x);
    else if(x>a[u])insert(ch[u][1],x);
    sz[u]++;
    balance(u);//添加一个点可能导致u的子树失衡
    return;
}
void del(int &u,int x)
{
    if(x<a[u])del(ch[u][0],x);
    else if(x>a[u])del(ch[u][1],x);
    sz[u]--;
    balance(u);//删除一个点可能导致u的子树失衡
    return;
}
int Rank(int u,int x)
{
    if(!u)return 0;
    if(x<a[u])return Rank(ch[u][0],x);
    else if(x>a[u])return sz[u]-sz[ch[u][1]]+Rank(ch[u][1],x);
    else return sz[ch[u][0]];
}
int find(int u,int x)
{
    if(x<=sz[ch[u][0]])return find(ch[u][0],x);
    else if(x>sz[u]-sz[ch[u][1]])return find(ch[u][1],x-sz[u]+sz[ch[u][1]]);
    else return a[u];
}
int main()
{
    scanf("%d",&n);
    for(int i=1,op,x;i<=n;i++)
    {
        scanf("%d%d",&op,&x);
        if(op==1)insert(rt,x);
        else if(op==2)del(rt,x);
        else if(op==3)printf("%d\n",Rank(rt,x)+1);
        else if(op==4)printf("%d\n",find(rt,x));
        else if(op==5)printf("%d\n",find(rt,Rank(rt,x)));
        else printf("%d\n",find(rt,Rank(rt,x+1)+1));
    }
    return 0;
}

WBLT

这颗平衡树好像很少有人写，但是它的功能是很多的，而且常数也不是很大，可能唯一的缺点就是要开两倍空间了吧。

WBLT 判断失衡的方法和替罪羊相似，都是设定一个阈值 $\alpha$，但它的判断方式是若 $min(sz[ch[u][0]],sz[ch[u][1]])<\alpha \times sz[u]$ 的话则失衡，阈值 $\alpha $ 一般设为 $0.25$。

WBLT 有两种维护平衡的方法，旋转和合并，这里我们给出旋转的方法。

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
const double alpha=0.25;
int n,rt,id,sz[N],val[N],ch[N][2];
int tot,bin[N];
int newnode(int s)
{
    int x;
    if(tot)x=bin[tot--];
    else x=++id;
    sz[x]=1,val[x]=s,ch[x][0]=ch[x][1]=0;
    return x;
}
void delnode(int &x)
{
    bin[++tot]=x,x=0;
    return;
}
void upd(int u)
{
    sz[u]=sz[ch[u][0]]+sz[ch[u][1]];
    val[u]=val[ch[u][1]];
    return;
}
int too_heavy(int x,int y){return y<alpha*(x+y);}
int double_rotate(int u,int r){return sz[ch[u][r]]>sz[u]/(2-alpha);}
void rotate(int &u,int r)
{
    int t=ch[u][r];
    ch[u][r]=ch[t][r^1];
    ch[t][r^1]=u;
    upd(u),upd(t),u=t;
    return;
}
void balance(int &u)
{
    int r=sz[ch[u][0]]<sz[ch[u][1]];
    if(!too_heavy(sz[ch[u][r]],sz[ch[u][r^1]]))return;
    if(sz[ch[u][r]]>1&&double_rotate(ch[u][r],(r^1)))rotate(ch[u][r],(r^1));
    rotate(u,r);
    return;
}
void insert(int &u,int x)
{
    if(!u){u=newnode(x);return;}
    else if(sz[u]==1)
    {
        int r=val[u]>x;
        ch[u][r]=newnode(val[u]),ch[u][r^1]=newnode(x),upd(u);
        return;
    }
    else if(x<=val[ch[u][0]])insert(ch[u][0],x);
    else insert(ch[u][1],x);
    upd(u),balance(u);
    return;
}
void del(int &u,int x)
{
    if(sz[u]==1){delnode(u);return;}
    int r=val[ch[u][0]]<x;
    del(ch[u][r],x);
    if(!ch[u][r])
    {
        int t=ch[u][!r];
        delnode(u);
        u=t;
        return;
    }
    upd(u),balance(u);
    return;
}
int Rank(int u,int x)
{
    if(!u)return 0;
    else if(sz[u]==1)return val[u]<x;
    else if(x<=val[ch[u][0]])return Rank(ch[u][0],x);
    else return sz[ch[u][0]]+Rank(ch[u][1],x);
}
int find(int u,int x)
{
    if(!u)return -1;
    else if(sz[u]==1)return val[u];
    else if(sz[ch[u][0]]>=x)return find(ch[u][0],x);
    else return find(ch[u][1],x-sz[ch[u][0]]);
}
int main()
{
    scanf("%d",&n);
    for(int i=1,op,x;i<=n;i++)
    {
        scanf("%d%d",&op,&x);
        if(op==1)insert(rt,x);
        else if(op==2)del(rt,x);
        else if(op==3)printf("%d\n",Rank(rt,x)+1);
        else if(op==4)printf("%d\n",find(rt,x));
        else if(op==5)printf("%d\n",find(rt,Rank(rt,x)));
        else printf("%d\n",find(rt,Rank(rt,x+1)+1));
    }
    return 0;
}

posted @ 2025-08-01 13:08 AvisD 阅读(57) 评论(3) 收藏举报

刷新页面返回顶部

Loading

AvisDJuruo

平衡树从入门到入土

平衡树从入门到入土

二叉搜索树

替罪羊树

WBLT

公告