福州市 2025 国庆集训 Day1 前三题题解
福州市 2025 国庆集训 Day1 前三题题解
别问为啥只有前三题,因为后面我不会……
T1 旅行
注意到 \(P\) 非常小,所以可以考虑指数级别的做法。
考虑状压 dp。设 \(f_{s,u}\) 表示经过 \(P\) 内的点集为 \(s\),当前位于 \(P\) 中第 \(u\) 号点的最短路径长度。
然而我们的路径其实是 \(1\rightarrow p_1\rightarrow \cdots \rightarrow p_n\rightarrow n\),所以其实点集的级别是 \(2^{p+2}\)。
那么转移就是枚举 \(s\),然后枚举 \(s\) 内经过的点 \(i\),再枚举 \(s\) 内没经过的点 \(j\),得到新的状态 s'=s|(1<<j)。
然后 \(f_{s',j}=\min \left\{f_{s,i}+dis_{p_i,p_j}\right\}\)。其中 \(dis_{p_i,p_j}\) 表示点 \(p_i\) 到点 \(p_j\) 的最短路径长度。可以用 Floyd 预处理出来。
最后的答案显然就是 \(f_{2^{p+2}-1,p+1}\)。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ljl;
const int N=205,M=1e4+5,P=15;
const ljl inf=1e18;
int n,m,p,vec[N],cur=1;
ljl dis[N][N],ans,f[(1<<P)+5][N];
bool vis[N];
int main(){
ios::sync_with_stdio(0);
cin>>n>>m;
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
if(i!=j)dis[i][j]=inf;
for(int i=1;i<=m;++i)
{
ljl u,v,w;
cin>>u>>v>>w;
dis[u][v]=dis[v][u]=min(dis[u][v],w);
}
cin>>p;
for(int i=1;i<=p;++i)
{
cin>>vec[i];
vis[vec[i]]=1;
}
vec[0]=1;vec[p+1]=n;
for(int k=1;k<=n;++k)
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
memset(f,0x3f,sizeof(f));f[1][0]=0;
for(int i=0;i<(1<<p+2);++i)
{
for(int j=0;j<p+2;++j)
{
if(!((i>>j)&1))continue;
for(int k=0;k<p+2;++k)
{
if((i>>k)&1)continue;
f[i|(1<<k)][k]=
min(f[i|(1<<k)][k],f[i][j]+dis[vec[j]][vec[k]]);
}
}
}
ans=f[(1<<p+2)-1][p+1];
if(ans>=inf)cout<<-1<<'\n';
else cout<<ans<<'\n';
return 0;
}
T2 种植
先看看如果不考虑 \(q_i\),那么就是个简单的 01 背包板子。
但是它有 \(q_i\) 啊?
我们可以尝试下,发现把 \(q_i\) 按照从大到小的顺序排序后依次插入是最优的。
证明听了,但不会。/kel。只懂把某个时间段移到前面,与前面的交换,则前面的也一定可以对答案做出贡献。所以不会更劣。
来自 hqh 巨佬的证明:
- 题目没要求固定的种植顺序,所以可以改变顺序。
- 因为q越大意味着在相同的室内栽培时间下,它剩出的时间最多,所以放在前面绝对不劣。
所以可以得出q从大到小排序必定为最优解。
先 orz 下。
我的理解:
因为我们种植完第 \(i\) 个后是要继续种植的,而继续种植的同时是可以让 \(i\) 在户外生长的,如果同时进行的时间最长,则消耗时间是最少的,所以最优。
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=305,T=2e4+5;
int n,t,f[T],ans;
struct NODE{
int p,q,r;
bool operator < (const NODE x)const{
return q>x.q;
}
}node[N];
int main(){
ios::sync_with_stdio(0);
cin>>n>>t;
for(int i=1;i<=n;++i)
cin>>node[i].p>>node[i].q>>node[i].r;
sort(node+1,node+n+1);
for(int i=1;i<=n;++i)
{
for(int j=t-node[i].q;j>=node[i].p;--j)
{
f[j]=max(f[j],f[j-node[i].p]+node[i].r);
}
}
for(int i=1;i<=t;++i)
ans=max(ans,f[i]);
cout<<ans<<'\n';
return 0;
}
T3 最短路
妙妙题。
考虑额外加边的本质是什么。
通过 T1,不难想到其实就是把数字化作二进制,看成集合,\(i\) 可以向 \(j\) 连边当且仅当 \(j\) 是 \(i\) 的真子集。
那么考虑怎么优化建图。
比如说当前数字为 \((101)_2\),那么可以 \((101)_2\rightarrow (100)_2\),以及 \((101)_2\rightarrow (001)_2\)。其中边权均为 \(0\)。
那么就有问题了:正常来说边权是 \(1\) 啊?
其实这些点都是虚图。点编号是从 \(n+1\) 开始的。
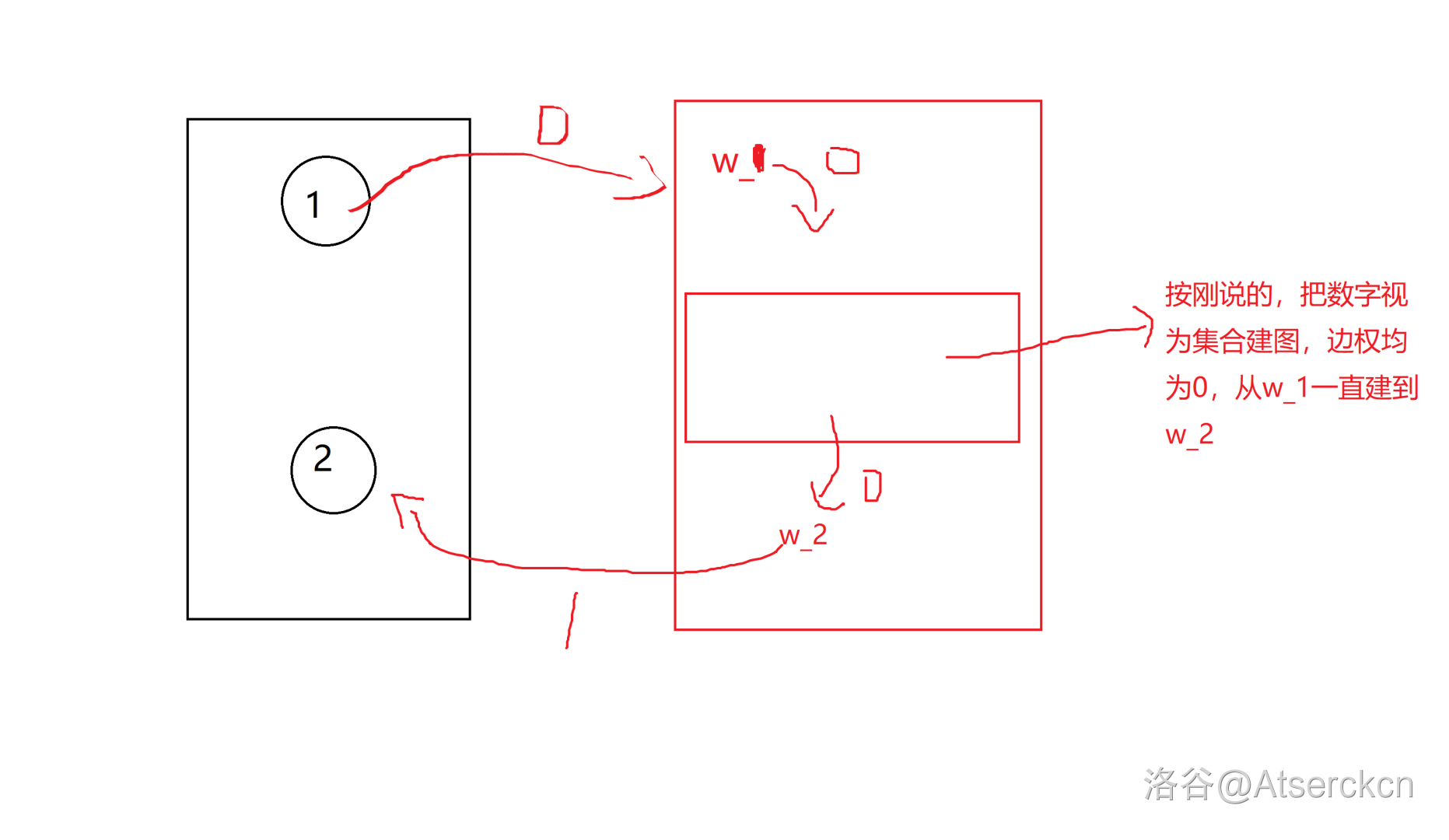
所以我们就建好了图。
注意,这样的话,需要开的点的大小是 \(2\times 10^5+2^{20}\),边是 \(3\times 10^5+2^{20}\times 20\)。
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+(1<<20)+5,M=3e5+(1<<20)*20+5;
int n,m,a[N],ehead[N],cnt_e,dis[N],maxa;
bool vis[N];
struct E{
int to,w,pre;
}e[M];
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > h;
void adde(int from,int to,int w)
{
e[++cnt_e].to=to;
e[cnt_e].w=w;
e[cnt_e].pre=ehead[from];
ehead[from]=cnt_e;
return;
}
void dijk()
{
memset(dis,0x3f,sizeof(dis));dis[1]=0;
h.push(make_pair(dis[1],1));
while(!h.empty())
{
int u=h.top().second;h.pop();
if(vis[u])continue;
vis[u]=1;
for(int i=ehead[u];i;i=e[i].pre)
{
int v=e[i].to,w=e[i].w;
if(dis[v]>dis[u]+w)
{
dis[v]=dis[u]+w;
if(!vis[v])h.push(make_pair(dis[v],v));
}
}
}
return;
}
int main(){
ios::sync_with_stdio(0);
cin>>n>>m;
for(int i=1;i<=n;++i)cin>>a[i];
for(int i=1,u,v;i<=m;++i)
{
cin>>u>>v;
adde(u,v,1);
}
for(int i=1;i<=n;++i)
adde(i,n+a[i]+1,0),adde(n+a[i]+1,i,1),maxa=max(maxa,a[i]);
for(int i=1;i<=maxa;++i)//set i
{
//set i->set j(j\in i)
for(int j=0;j<20;++j)
{
if((i>>j)&1)adde(n+i+1,n+(i^(1<<j))+1,0);
}
}
dijk();
for(int i=1;i<=n;++i)
cout<<(dis[i]==0x3f3f3f3f?-1:dis[i])<<'\n';
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号