HOG算法以及python实现

HOG(Histogram of Oreinted Gradients) 方向梯度直方图是一种常用的图像特征算法，和SVM等机器学习算法一起使用可以实现目标检测等。本文详细介绍HOG并给出python的MNIST实例。

参考：

• https://zhuanlan.zhihu.com/p/85829145
• https://iq.opengenus.org/object-detection-with-histogram-of-oriented-gradients-hog/
• https://scikit-image.org/docs/stable/auto_examples/features_detection/plot_hog.html

HOG算法介绍

译文：Navneet Dalal和Bill Triggs在2005年提出了方向梯度直方图(HOG)特征。HOG是一种用于图像处理的特征描述符，主要用于目标检测。特征描述符是图像或图像patch的表示，它通过从图像中提取有用信息来简化图像。HOG的原理是通过灰度梯度或边缘方向的分布来描述图像中局部物体的外观和形状。图像的x和y导数(梯度)是有用的，因为由于强度的突变，边缘和角落的梯度的幅度很大，我们知道边缘和角落比平坦区域包含更多关于物体形状的信息。因此，梯度方向的直方图（HOG）被用作描述符的特征。

方向梯度

对于图像上的一个像素点，其方向梯度的值由其上下左右4个点决定，可以计算为幅值$g$和方向$\theta$，公式如下:

$g = \sqrt {g_x^2 + g_y^2} \\ \theta = \text {arctan} \frac {g_y}{g_x}$

以下图为例，点Q的周围4个像素点值如下：

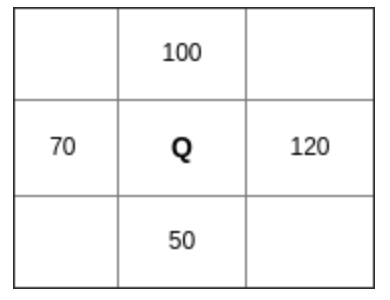
有：
$g_x = 120-70=50$
$g_y = 100-50=50$
$g = \sqrt {g_x^2 + g_y^2}=70.7$
$\theta = \text {arctan} \frac {g_y}{g_x}=\ang{45}$

梯度直方图

梯度直方图是在一个$8^2$的cell里面计算的。那么在$8^2$的cell里面就会有$8*8*2=128$个值，2是包括了梯度强度和梯度方向。通过统计形成梯度直方图，128个值将会变成9个值，大大降低了计算量，同时又对光照等环境变化更加地robust。

首先，我将0-180度分成9个bins，分别是0，20，40...160。然后统计每一个像素点所在的bin。请看下图：

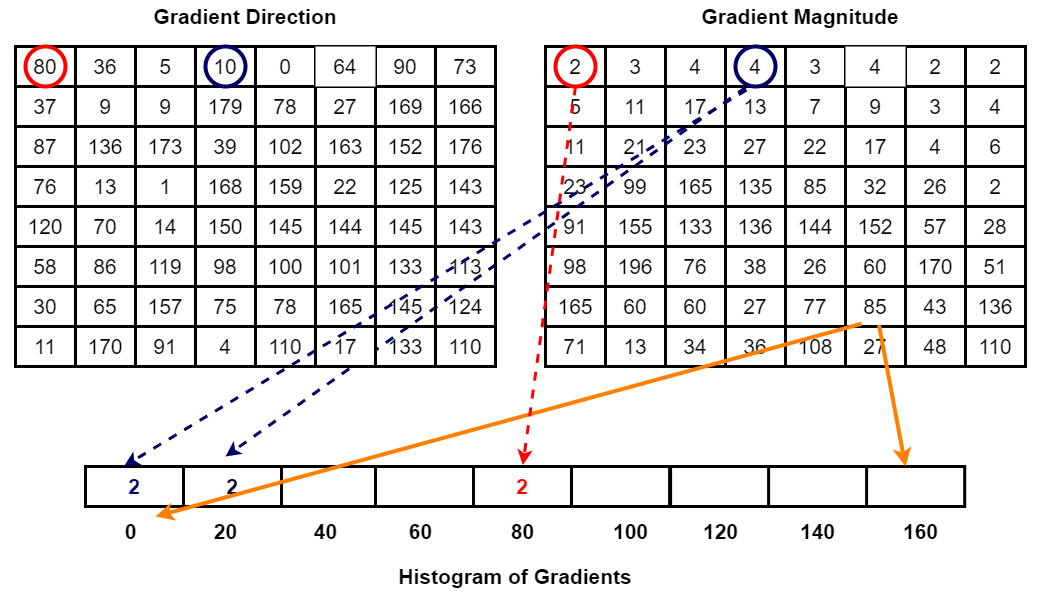
比如上面方向图中红圈包围的像素，角度为80度，这个像素对应的幅值为2，所以在直方图80度对应的bin加上2。蓝圈包围的像素，角度为10度，介于0度和20度之间，其幅值为4，那么这个梯度值就被按比例分给0度和20度对应的bin，也就是各加上2。

还有一个细节需要注意，如果某个像素的梯度角度大于160度，也就是在160度到180度之间，那么把这个像素对应的梯度值按比例分给0度和160度对应的bin。

将这 8x8 的cell中所有像素的梯度值加到各自角度对应的bin中，就形成了长度为9的直方图。

BLOCK归一化

HOG将8×8的一个区域作为一个cell，再以2×2个cell作为一组，称为block。由于每个cell有9个值，2×2个cell则有36个值，HOG是通过滑动窗口的方式来得到block的，如下图所示：

在前面的步骤中，我们基于图像的梯度对每个cell创建了一个直方图。

但是图像的梯度对整体光照非常敏感，比如通过将所有像素值除以2来使图像变暗，那么梯度幅值将减小一半，因此直方图中的值也将减小一半。 理想情况下，我们希望我们的特征描述符不会受到光照变化的影响，那么我们就需要将直方图“归一化” 。

在说明如何归一化直方图之前，先看看长度为3的向量是如何归一化的。

假设我们有一个向量 [128,64,32]，向量的长度为$\sqrt {128^2 + 64^2 + 32^2}=146.64$，这叫做向量的L2范数。将这个向量的每个元素除以146.64就得到了归一化向量 [0.87, 0.43, 0.22]。

现在有一个新向量，是第一个向量的2倍 [128x2, 64x2, 32x2]，也就是 [256, 128, 64]，我们将这个向量进行归一化，你可以看到归一化后的结果与第一个向量归一化后的结果相同。所以，对向量进行归一化可以消除整体光照的影响。

知道了如何归一化，现在来对block的梯度直方图进行归一化（注意不是cell），一个block有4个直方图，将这4个直方图拼接成长度为36的向量，然后对这个向量进行归一化。

因为使用的是滑动窗口，滑动步长为8个像素，所以每滑动一次，就在这个窗口上进行归一化计算得到长度为36的向量，并重复这个过程。

Python实例

官方示例

scikit-image.feature中包含了hog特征
https://scikit-image.org/docs/stable/api/skimage.feature.html#skimage.feature.hog
以下是官方示例：

import matplotlib.pyplot as plt

from skimage.feature import hog
from skimage import data, exposure


image = data.astronaut()

fd, hog_image = hog(image, orientations=8, pixels_per_cell=(16, 16),
                    cells_per_block=(1, 1), visualize=True, channel_axis=-1)

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4), sharex=True, sharey=True)

ax1.axis('off')
ax1.imshow(image, cmap=plt.cm.gray)
ax1.set_title('Input image')

# Rescale histogram for better display
hog_image_rescaled = exposure.rescale_intensity(hog_image, in_range=(0, 10))

ax2.axis('off')
ax2.imshow(hog_image_rescaled, cmap=plt.cm.gray)
ax2.set_title('Histogram of Oriented Gradients')
plt.show()

这里图片的像素是$512 * 512$，我们如果打印fd.shape，会得到结果为8192。
这是因为512的像素除以16得到每个边分为32份，计算$32 * 32$得到1024。在这里设置orientations=8,即每个cell直方图分为8等分，得到结果$1024 * 8 = 8192$

用于FMNIST分类

下面示例HOG结合SVM做经典的FMNIST分类，数据源于TensorFlow。

# import files
data_train_file = "./Datasets/fashion-mnist_train.csv"
data_test_file = "./Datasets/fashion-mnist_test.csv"

# read files csv
df_train = pd.read_csv(data_train_file)
df_test = pd.read_csv(data_test_file)

# data as array in order to reshape them
train_data = np.array(df_train, dtype='float32')
test_data = np.array(df_test, dtype='float32')

train_len = train_data.shape[0]

FEATURE = np.zeros([train_len, fd.shape[0]])
LABEL = []

for i in range(train_len):
    pic = train_data[i,1:].reshape(28,28).astype('uint8')
    img = cv2.cvtColor(pic, cv2.COLOR_GRAY2BGR)
    hv = hog(img, orientations=8, pixels_per_cell=(4, 4),
             cells_per_block=(1, 1), visualize=False, channel_axis=-1)
    FEATURE[i] = hv
    LABEL.append(train_data[i,0])
	
test_len = test_data.shape[0]

TEST_FEATURE = np.zeros([test_len, fd.shape[0]])
TEST_LABEL = []

for i in range(test_len):
    pic = test_data[i,1:].reshape(28,28).astype('uint8')
    img = cv2.cvtColor(pic, cv2.COLOR_GRAY2BGR)
    hv = hog(img, orientations=8, pixels_per_cell=(4, 4),
             cells_per_block=(1, 1), visualize=False, channel_axis=-1)
    TEST_FEATURE[i] = hv
    TEST_LABEL.append(test_data[i,0])
	
# Linear svc 分类
from sklearn.svm import LinearSVC
clf = LinearSVC(max_iter=10000)
clf.fit(FEATURE, LABEL)

clf.score(TEST_FEATURE, TEST_LABEL)