二叉树
什么是二叉树
当我们得到一个数,就将这个数放在第一位,拿到第二个数时,对比第一个数,小则放在左边(左孩子Left),大则放在右边(Right),接下来依次类推。
- 深度优先遍历DFS:(栈)递归方法
- 前序遍历(Pre—Order)(根左右)
- 中序遍历(In-Order)(左根右)会让树按顺序排列
- 后序遍历 (Post—Order)(左右根)
- 广度优先遍历(层次遍历)队列方法
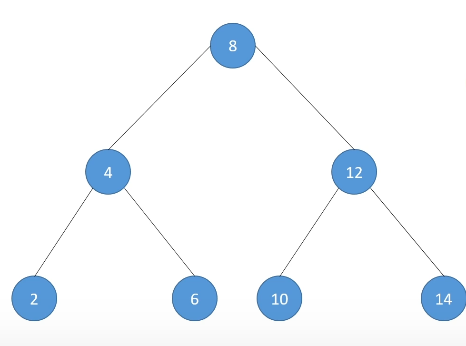
给你一个数组int[] a=new int[]{8,4,12,2,6,10,14};
经过一些排序后得到类似于这样一颗倒转过来的数型图
完整代码:
Tree.cs
class Tree<T> where T:IComparable<T>
{
private class Node
{
public T Val { get; set; }
public Node Left { get; set; }
public Node Right { get; set; }
public Node(T val)
{
this.Val=val;
this.Left=null;
this.Right=null;
}
}
private Node root; //我们的根节点
private int N; //存储元素的个数
public Tree() //当我们实例一个对象时候初始化
{
root=null;
N=0;
}
public int Count { get{return N;} }
public bool IsEmpty {get{return N==0;}} //N为0代表没有节点
//非递归添加元素
public void add(T val)
{
if(root==null)
{
root=new Node(val);
N++;
return;
}
Node pre=null;
Node cur=root;
while(cur!=null)
{
if(val.CompareTo(cur.Val)==0) return;
pre=cur;
if(val.CompareTo(cur.Val)<0)
{
cur=cur.Left;
}
else if(val.CompareTo(cur.Val)>0)
{
cur=cur.Right;
}
}
cur=new Node(val); //当cur所指向的节点为空时,创建新叶子
if(val.CompareTo(pre.Val)<0)
{
pre.Left=cur;
}else
{
pre.Right=cur;
}
N++; //多了一个元素
}
//递归方式添加新元素
public void Add(T val)
{
root=Add(root,val);
}
private Node Add(Node Root,T val)
{
if(Root==null)
{
N++;
return new Node(val);
}
if(val.CompareTo(Root.Val)<0)
{
Root.Left=Add(Root.Left,val); //递归到最后会返回一个Node节点,用left去接住
}
if(val.CompareTo(Root.Val)>0)
{
Root.Right=Add(Root.Right,val); //同理
}
return Root;
}
//查找元素
public bool Contains(T val)
{
return Contains(root,val);
}
private bool Contains(Node Root,T val)
{
if(Root==null)
{
return false;
}
if(val.CompareTo(Root.Val)==0)
{
return true;
}
else if(val.CompareTo(Root.Val)<0)
{
return Contains(Root.Left,val);
}
else
{
return Contains(Root.Right,val);
}
}
//前序遍历(PreOrder) 根左右
public void PreOrder()
{
PreOrder(root);
}
private void PreOrder(Node Root)
{
if(Root==null)
{
return;
}
System.Console.WriteLine(Root.Val);
PreOrder(Root.Left);
PreOrder(Root.Right);
}
//中序遍历(In-Order)左根右
public void InOrder()
{
InOrder(root);
}
private void InOrder(Node Root)
{
if(Root==null)
{
return;
}
InOrder(Root.Left);
System.Console.WriteLine(Root.Val);
InOrder(Root.Right);
}
//后序遍历(Post-Order)
public void PostOrder()
{
PostOrder(root);
}
private void PostOrder(Node Root)
{
if(Root==null)
{
return;
}
PostOrder(Root.Left);
PostOrder(Root.Right);
System.Console.WriteLine(Root.Val);
}
//广度优先遍历(层次遍历)
public void LevelOrder()
{
LevelOrder(root);
}
private void LevelOrder(Node Root)
{
Queue<Node> q=new Queue<Node>();
q.Enqueue(root);
while(q.Count!=0)
{
Node cur=q.Dequeue();
System.Console.WriteLine(cur.Val);
if(cur.Left!=null)
{
q.Enqueue(cur.Left);
}
if(cur.Right!=null)
{
q.Enqueue(cur.Right);
}
}
}
//查找最小值
public T Min()
{
if(root==null)
{
throw new ArgumentException("空树");
}
return Min(root).Val;
}
private Node Min(Node Root)
{
if(Root.Left==null)
{
return Root;
}
return Min(Root.Left);
}
//查找最大值
public T Max()
{
if(root==null)
{
throw new ArgumentException("空树");
}
return Max(root).Val;
}
private Node Max(Node Root)
{
if(Root.Right==null)
{
return Root;
}
return Max(Root.Right);
}
//删除最小值,最大值
public T RemoveMin()
{
T val=Min();
RemoveMin(root);
return val;
}
private Node RemoveMin(Node Root)
{
if(Root.Left==null)
{
N--;
return Root.Right;
}
Root.Left=RemoveMin(Root.Left);
return Root;
}
public T RemoveMax()
{
T val=Max();
RemoveMax(root);
return val;
}
private Node RemoveMax(Node Root)
{
if(Root.Right==null)
{
N--;
return Root.Left;
}
Root.Right=RemoveMax(Root.Right);
return Root;
}
//删除任意节点
public void Remove(T e)
{
root=Remove(root,e);
}
private Node Remove(Node Root,T e)
{
if(Root==null) return null;
if(e.CompareTo(Root.Val)<0)
{
Root.Left=Remove(Root.Left,e);
return Root;
}
else if(e.CompareTo(Root.Val)>0)
{
Root.Right=Remove(Root.Right,e);
return Root;
}
else
{
if(Root.Left==null)
{
N--;
return Root.Right;
}
if(Root.Right==null)
{
N--;
return Root.Left;
}
Node s=Min(Root.Right);
s.Right=RemoveMin(Root.Right);
s.Left=Root.Left;
return s;
}
}
//树的高度取值
public int MaxHeight()
{
return MaxHeight(root);
}
private int MaxHeight(Node Root)
{
if(Root==null) return 0;
int l=MaxHeight(Root.Left);
int r=MaxHeight(Root.Right);
return Math.Max(l,r)+1;
}
}
Program.cs
class Test
{
static void Main(string[] arg)
{
int[] a=new int[]{8,4,12,2,6,10,14};
Tree<int> tree=new Tree<int>();
for(int i=0;i<a.Length;i++)
{
tree.Add(a[i]);
}
int maxH=tree.MaxHeight();
System.Console.WriteLine(maxH);
// tree.PreOrder(); //前序深度优先遍历
// System.Console.WriteLine("=========");
// tree.InOrder(); //中序深度优先遍历
// System.Console.WriteLine("=========");
// tree.PostOrder(); //后序深度优先遍历
// System.Console.WriteLine("=========");
// tree.LevelOrder(); //广度优先遍历
// System.Console.WriteLine("=========");
// System.Console.WriteLine(tree.Min());
// System.Console.WriteLine("=========");
// System.Console.WriteLine(tree.Max());
// System.Console.WriteLine(tree.Count);
//System.Console.WriteLine("删除了最小值{0}",tree.RemoveMin());
// System.Console.WriteLine("删除了最大值{0}",tree.RemoveMax());
// System.Console.WriteLine(tree.Count);
// tree.Remove(12);
// tree.InOrder(); //中序深度优先遍历
}
}
如何添加新元素
非递归的方法:
首先创建一个cur指针与pre指针,pre是跟在cur后面的,当有一个数字进来时候,如果还是空树,则初始化root,不是则对root进行比较,小则在Left,大则在Left,先让pre等于cur,再让cur去移动,当移动到一个null值时候,退出循环,cur此时new个新节点,cur的值与pre比较,小则将pre的左孩子=cur,大则将pre的右孩子=cur
递归:
当传进来的根为null值时,则创建新值并初始化,如果有根,则再衍生,通过递归对比数字,达到合适的位置返回一个Node节点,完成添加。
前序深度优先遍历
先打印根的值,在递归左孩子,再递归右孩子
点击查看代码
private void PreOrder(Node Root)
{
if(Root==null)
{
return;
}
System.Console.WriteLine(Root.Val);
PreOrder(Root.Left);
PreOrder(Root.Right);
}
中序深度优先遍历
先递归左孩子,然后递归到左孩子为null时候,返回到打印当前根的值,再进入右孩子递归,适合来做二叉树的顺序查找
点击查看代码
private void InOrder(Node Root)
{
if(Root==null)
{
return;
}
InOrder(Root.Left);
System.Console.WriteLine(Root.Val);
InOrder(Root.Right);
}
后序深度优先遍历
先递归左孩子,再右孩子,最后打印值根的值
点击查看代码
private void PostOrder(Node Root)
{
if(Root==null)
{
return;
}
PostOrder(Root.Left);
PostOrder(Root.Right);
System.Console.WriteLine(Root.Val);
}
广度优先遍历
利用队列,不用递归,也就不增加函数调用栈,是一种层级遍历,对于树的高度太庞大时使用,主要思想就是加二打一
首先把根加进队列,写个循环,当队列的值不为空时,将值拿出,打印,之后加入左孩子与右孩子进队列,以此循环,直到队列没有节点
点击查看代码
private void LevelOrder(Node Root)
{
Queue<Node> q=new Queue<Node>();
q.Enqueue(root);
while(q.Count!=0)
{
Node cur=q.Dequeue();
System.Console.WriteLine(cur.Val);
if(cur.Left!=null)
{
q.Enqueue(cur.Left);
}
if(cur.Right!=null)
{
q.Enqueue(cur.Right);
}
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号