一、聚类
1.聚类的定义
将物理或抽象对象的集合分成由类似的对象组成的多个类的过程被称为聚类。由聚类所生成的簇是一组数据对象的集合,这些对象与同一个簇中的对象彼此相似,与其他簇中的对象相异。
通俗的讲,聚类是按照某个特定标准(如距离)把一个数据集分割成不同的类或簇,使得同一个簇内的数据对象的相似性尽可能大,同时不在同一个簇中的数据对象的差异性也尽可能地大。也即聚类后同一类的数据尽可能聚集到一起,不同类数据尽量分离。
2.聚类的目标
3. 聚类的一般过程
① 数据准备:特征标准化和降维
② 特征选择:从最初的特征中选择最有效的特征,并将其存储在向量中
③ 特征提取:通过对选择的特征进行转换形成新的突出特征
④ 聚类:基于某种距离函数进行相似度度量,获取簇
⑤ 聚类结果评估:分析聚类结果,如距离误差和(SSE)等
4.聚类方法分类
① 划分方法(partitioning methods):K-MEANS算法、K-MEDOIDS算法、CLARANS算法
划分方法给定一个有N个元组或者纪录的数据集,分裂法将构造K个分组,每一个分组就代表一个聚类,K<N。而且这K个分组满足下列条件:(1) 每一个分组至少包含一个数据纪录;(2)每一个数据纪录属于且仅属于一个分组(注意:这个要求在某些模糊聚类算法中可以放宽);对于给定的K,算法首先给出一个初始的分组方法,以后通过反复迭代的方法改变分组,使得每一次改进之后的分组方案都较前一次好,而所谓好的标准就是:同一分组中的记录越近越好,而不同分组中的纪录越远越好。
② 层次方法(hierarchical methods):BIRCH算法、CURE算法、CHAMELEON算法
层次方法对给定的数据集进行层次似的分解,直到某种条件满足为止。具体又可分为“自底向上”和“自顶向下”两种方案。例如在“自底向上”方案中,初始时每一个数据纪录都组成一个单独的组,在接下来的迭代中,它把那些相互邻近的组合并成一个组,直到所有的记录组成一个分组或者某个条件满足为止。
③ 基于密度的方法(density-based methods):DBSCAN算法、OPTICS算法、DENCLUE算法
划分和层次的方法旨在发现球状簇,他们很难形成任意形状的簇,因此无法根据数据的特征进行聚合,为了发现任意形状的簇,我们可以把簇看做数据空间中被稀疏区域分开的稠密区,这样就能克服基于距离的算法只能发现“类圆形”的聚类的缺点。这个方法的指导思想就是,只要一个区域中的点的密度大过某个阀值,就把它加到与之相近的聚类中去。
④ 基于网格的方法(grid-based methods):STING算法、CLIQUE算法、WAVE-CLUSTER算法
基于网格的方法首先将数据空间划分成为有限个单元(cell)的网格结构,所有的处理都是以单个的单元为对象的。这么处理的一个突出的优点就是处理速度很快,通常这是与目标数据库中记录的个数无关的,它只与把数据空间分为多少个单元有关。
⑤ 基于模型的方法(model-based methods):统计的方案和神经网络的方案
基于模型的方法给每一个聚类假定一个模型,然后去寻找能够很好的满足这个模型的数据集。这样一个模型可能是数据点在空间中的密度分布函数或者其它。它的一个潜在的假定就是:目标数据集是由一系列的概率分布所决定的。
⑥ 其他聚类方法:传递闭包法,布尔矩阵法,直接聚类法,相关性分析聚类,基于统计的聚类方法
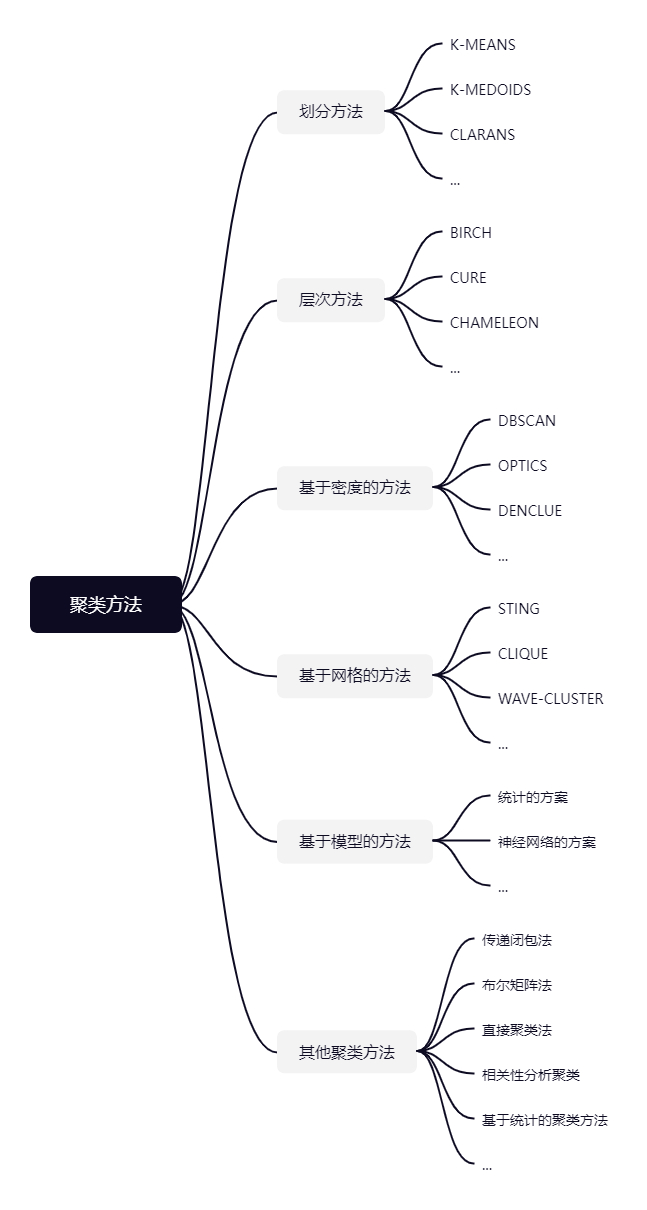
图1 聚类方法思维导图
二、常用聚类方法及python实现
0.准备工作
①加载包

1 ## 输出高清图像 2 %config InlineBackend.figure_format = 'retina' 3 %matplotlib inline 4 ## 图像显示中文的问题 5 import matplotlib 6 matplotlib.rcParams['axes.unicode_minus']=False 7 8 import seaborn as sns 9 sns.set(font= "Kaiti",style="ticks",font_scale=1.4) 10 11 ## 忽略提醒 12 import warnings 13 warnings.filterwarnings("ignore") 14 15 ## 导入会使用到的相关库 16 import numpy as np 17 import pandas as pd 18 import matplotlib.pyplot as plt 19 from mpl_toolkits.mplot3d import Axes3D 20 import seaborn as sns 21 22 from sklearn.manifold import TSNE 23 from sklearn.preprocessing import StandardScaler 24 from sklearn.datasets import load_wine 25 from sklearn.cluster import * 26 from sklearn.metrics.cluster import v_measure_score 27 from sklearn.metrics import * 28 from sklearn.mixture import GaussianMixture,BayesianGaussianMixture 29 from sklearn.neighbors import LocalOutlierFactor 30 from sklearn.model_selection import train_test_split,GridSearchCV 31 from sklearn.svm import OneClassSVM 32 33 from pyclustering.cluster.kmedians import kmedians 34 from pyclustering.cluster.fcm import fcm 35 from pyclustering.cluster import cluster_visualizer 36 37 from scipy.cluster import hierarchy 38 39 import networkx as nx 40 from networkx.drawing.nx_agraph import graphviz_layout 41 42 import pyod.models as pym 43 from pyod.models.cof import COF 44 from pyod.models.pca import PCA 45 from pyod.models.sod import SOD 46 from pyod.models.iforest import IForest 47 from pyod.models.xgbod import XGBOD
②加载数据

1 ## 对酒数据的TSNE降维后的结果进行聚类分析 2 3 ## 对酒的特征数据进行标准化 4 wine_x,wine_y = load_wine(return_X_y=True) 5 wine_x = StandardScaler().fit_transform(wine_x) 6 print("每类样本数量:",np.unique(wine_y,return_counts = True)) 7 8 ## TSNE进行数据的降维,降维到3维空间中 9 tsne = TSNE(n_components = 3,perplexity =25, 10 early_exaggeration =3,random_state=123) 11 12 ## 获取降维后的数据 13 tsne_wine_x = tsne.fit_transform(wine_x) 14 print(tsne_wine_x.shape)
TSNE详见https://scikitlearn.org/stable/modules/generated/sklearn.manifold.TSNE.html
1.K-MEANS(https://www.cnblogs.com/pinard/p/6164214.html)
①原理
对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大。如果用数据表达式表示,假设簇划分为(C1,C2,...,Ck),则算法的目标是最小化平方误差E:
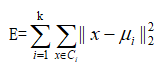
其中μi是簇Ci的均值向量,有时也称为质心,表达式为:
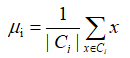
②算法流程
1)k值选择
一般来说,会根据对数据的先验经验选择一个合适的k值,如果没有什么先验知识,则可以通过交叉验证选择一个合适的k值。

1 ## 使用肘方法搜索合适的聚类数目 2 kmax = 10 3 K = np.arange(1,kmax) 4 iner = [] ## 类内误差平方和 5 for ii in K: 6 kmean = KMeans(n_clusters=ii,random_state=1) 7 kmean.fit(tsne_wine_x) 8 ## 计算类内误差平方和 9 iner.append(kmean.inertia_) 10 ## 可视化类内误差平方和的变化情况 11 plt.figure(figsize=(10,6)) 12 plt.plot(K,iner,"r-o") 13 plt.xlabel("聚类数目") 14 plt.ylabel("类内误差平方和") 15 plt.title("K-means聚类") 16 ## 在图中添加一个箭头 17 plt.annotate("转折点", xy=(3,iner[2]),xytext=(4,iner[2] + 2000), 18 arrowprops=dict(facecolor='blue', shrink=0.1)) 19 plt.grid() 20 plt.show()
2)质心选择
k个初始化的质心的位置选择对最后的聚类结果和运行时间都有很大的影响,因此需要选择合适的k个质心,最好这些质心不能太近。
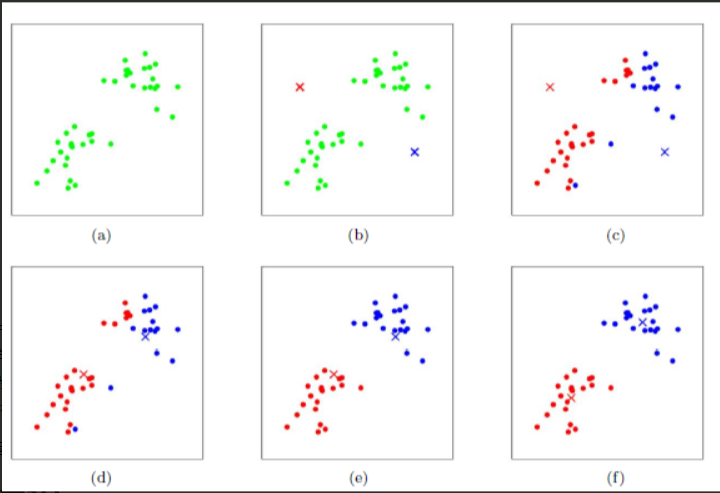
图2 k-means算法质心选择
图a表达了初始的数据集,假设k=2。在图b中,随机选择了两个k类所对应的类别质心,即图中的红色质心和蓝色质心,然后分别求样本中所有点到这两个质心的距离,并标记每个样本的类别为和该样本距离最小的质心的类别,如图c所示,经过计算样本和红色质心和蓝色质心的距离,我们得到了所有样本点的第一轮迭代后的类别。此时我们对我们当前标记为红色和蓝色的点分别求其新的质心,如图4所示,新的红色质心和蓝色质心的位置已经发生了变动。图e和图f重复了我们在图c和图d的过程,即将所有点的类别标记为距离最近的质心的类别并求新的质心。最终我们得到的两个类别如图f。
在实际K-Means算法中,我们一般会多次运行图c和图d,才能达到最终的比较优的类别。
传统K-MEANS算法流程:
输入是样本集D={x1,x2,...xm},聚类的簇树k,最大迭代次数N
输出是簇划分C={C1,C2,...Ck}
1) 从数据集D中随机选择k个样本作为初始的k个质心向量: {μ1,μ2,...,μk}
2)对于n=1,2,...,N
a) 将簇划分C初始化为Ct=∅ t=1,2...k
b) 对于i=1,2...m,计算样本xi和各个质心向量μj(j=1,2,...,k)的距离:dij=||xi−μj||22,将xi标记最小的为dij所对应的类别λi。此时更新Cλi=Cλi∪{xi}
c) 对于j=1,2,...,k,对Cj中所有的样本点重新计算新的质心μj
e) 如果所有的k个质心向量都没有发生变化,则转到步骤3)
3) 输出簇划分C={C1,C2,...,Ck}
③算法优缺点
K-Means的主要优点有:
1)原理比较简单,实现比较容易,收敛速度快。
2)聚类效果较优。
3)算法的可解释度比较强。
4)只需要调节参数簇数k。
K-Means的主要缺点有:
1)K值的选取不好把握
2)对于不是凸的数据集比较难收敛
3)如果各隐含类别的数据不平衡,比如各隐含类别的数据量严重失衡,或者各隐含类别的方差不同,则聚类效果不佳。
4)采用迭代方法,得到的结果只是局部最优。
5)对噪音和异常点比较的敏感。
④python代码
1)python实现
Clustering 详见 https://mathpretty.com/9374.html

1 ## 将数据聚类为3类并可视化相关结果 2 ## 使用KMeans将数据聚类为3类 3 kmean = KMeans(n_clusters=3,random_state=1) 4 k_pre = kmean.fit_predict(tsne_wine_x) 5 print("每簇包含的样本数量:",np.unique(k_pre,return_counts = True)) 6 print("每个簇的聚类中心为:\n",kmean.cluster_centers_) 7 print("聚类效果V测度: %.4f"%v_measure_score(wine_y,k_pre)) 8 9 ## 该得分是聚类同质性和完整性的调和平均数,越接近于1,说明聚类的效果越好, 10 # 同质性(Homogeneity): 每个聚类(簇)里面只包含单个类的样本。 11 # 完备性(completeness): 一个给定类的所有样本都被分到了同一个聚类(簇)中。 12 13 ## 使用Kmedians将数据聚类为3类 14 initial_centers = tsne_wine_x[[1,51,100],:] 15 np.random.seed(10) 16 kmed = kmedians(data=tsne_wine_x,initial_medians = initial_centers) 17 kmed.process() # 算法训练数据 18 kmed_pre = kmed.get_clusters() # 聚类结果 19 kmed_center = np.array(kmed.get_medians()) 20 ## 将聚类结果处理为类别标签 21 kmed_pre_label = np.arange(len(tsne_wine_x)) 22 for ii,li in enumerate(kmed_pre): 23 kmed_pre_label[li] = ii 24 25 print("每簇包含的样本数量:",np.unique(kmed_pre_label,return_counts = True)) 26 print("每个簇的聚类中心为:\n",kmed_center) 27 print("聚类效果V测度: %.4f"%v_measure_score(wine_y,kmed_pre_label)) 28 29 ## 该得分是聚类同质性和完整性的调和平均数,越接近于1,说明聚类的效果越好 30 31 ## 在3D空间中可视化聚类后的数据空间分布 32 colors = ["red","blue","green"] 33 shapes = ["o","s","*"] 34 fig = plt.figure(figsize=(15,6)) 35 ## 将坐标系设置为3D,K均值聚类结果 36 ax1 = fig.add_subplot(121, projection="3d") 37 for ii,y in enumerate(k_pre): 38 ax1.scatter(tsne_wine_x[ii,0],tsne_wine_x[ii,1],tsne_wine_x[ii,2], 39 s = 40,c = colors[y],marker = shapes[y],alpha = 0.5) 40 ## 可视化聚类中心 41 for ii in range(len(np.unique(k_pre))): 42 x = kmean.cluster_centers_[ii,0] 43 y = kmean.cluster_centers_[ii,1] 44 z = kmean.cluster_centers_[ii,2] 45 ax1.scatter(x,y,z,c = "gray",marker="o",s=150,edgecolor='k') 46 ax1.text(x,y,z,"簇"+str(ii+1)) 47 ax1.set_xlabel("特征1",rotation=20) 48 ax1.set_ylabel("特征2",rotation=-20) 49 ax1.set_zlabel("特征3",rotation=90) 50 ax1.azim = 225 51 ax1.set_title("K-means聚为3簇") 52 53 ## K中位数聚类结果 54 ax2 = fig.add_subplot(122, projection="3d") 55 for ii,y in enumerate(kmed_pre_label): 56 ax2.scatter(tsne_wine_x[ii,0],tsne_wine_x[ii,1],tsne_wine_x[ii,2], 57 s = 40,c = colors[y],marker = shapes[y],alpha = 0.5) 58 for ii in range(len(np.unique(kmed_pre_label))): 59 x = kmed_center[ii,0] 60 y = kmed_center[ii,1] 61 z = kmed_center[ii,2] 62 ax2.scatter(x,y,z,c = "gray",marker="o",s=150,edgecolor='k') 63 ax2.text(x,y,z,"簇"+str(ii+1)) 64 65 ax2.set_xlabel("特征1",rotation=20) 66 ax2.set_ylabel("特征2",rotation=-20) 67 ax2.set_zlabel("特征3",rotation=90) 68 ax2.azim = 225 69 ax2.set_title("K-medians聚为3簇") 70 plt.tight_layout() 71 plt.show()
2)评价指标
轮廓系数:是聚类效果好坏的一种评价方式,结合内聚度和分离度两种因素。可以用来在相同原始数据的基础上用来评价不同算法、或者算法不同运行方式对聚类结果所产生的影响。
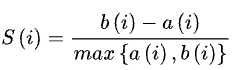

1 ## 使用轮廓系数评价聚类效果的好坏 2 ## 计算整体的平均轮廓系数,K均值 3 sil_score = silhouette_score(tsne_wine_x,k_pre) 4 ## 计算每个样本的silhouette值,K均值 5 sil_samp_val = silhouette_samples(tsne_wine_x,k_pre) 6 7 ## 可视化聚类分析轮廓图,K均值 8 plt.figure(figsize=(10,6)) 9 y_lower = 10 10 n_clu = len(np.unique(k_pre)) 11 for ii in np.arange(n_clu): ## 聚类为了3类 12 ## 将第ii类样本的silhouette值放在一块排序 13 iiclu_sil_samp_sort = np.sort(sil_samp_val[k_pre == ii]) 14 ## 计算第ii类的数量 15 iisize = len(iiclu_sil_samp_sort) 16 y_upper = y_lower + iisize 17 ## 设置ii类图像的颜色 18 color = plt.cm.Spectral(ii / n_clu) 19 plt.fill_betweenx(np.arange(y_lower,y_upper),0,iiclu_sil_samp_sort, 20 facecolor = color,alpha = 0.7) 21 # 簇对应的y轴中间添加标签 22 plt.text(-0.08,y_lower + 0.5*iisize,"簇"+str(ii+1)) 23 ## 更新 y_lower 24 y_lower = y_upper + 5 25 ## 添加平均轮廓系数得分直线 26 plt.axvline(x=sil_score,color="red",label = "mean:"+str(np.round(sil_score,3))) 27 plt.xlim([-0.1,1]) 28 plt.yticks([]) 29 plt.legend(loc = 1) 30 plt.xlabel("轮廓系数得分") 31 plt.ylabel("聚类标签") 32 plt.title("K-means聚类轮廓图") 33 plt.show() 34 35 ## 使用轮廓系数评价聚类效果的好坏 36 ## 计算整体的平均轮廓系数,K中位数 37 sil_score = silhouette_score(tsne_wine_x,kmed_pre_label) 38 ## 计算每个样本的silhouette值,K中位数 39 sil_samp_val = silhouette_samples(tsne_wine_x,kmed_pre_label) 40 41 ## 可视化聚类分析轮廓图,K中位数 42 plt.figure(figsize=(10,6)) 43 y_lower = 10 44 n_clu = len(np.unique(kmed_pre_label)) 45 for ii in np.arange(n_clu): ## 聚类为了3类 46 ## 将第ii类样本的silhouette值放在一块排序 47 iiclu_sil_samp_sort = np.sort(sil_samp_val[kmed_pre_label == ii]) 48 ## 计算第ii类的数量 49 iisize = len(iiclu_sil_samp_sort) 50 y_upper = y_lower + iisize 51 ## 设置ii类图像的颜色 52 color = plt.cm.Spectral(ii / n_clu) 53 plt.fill_betweenx(np.arange(y_lower,y_upper),0,iiclu_sil_samp_sort, 54 facecolor = color,alpha = 0.7) 55 # 簇对应的y轴中间添加标签 56 plt.text(-0.08,y_lower + 0.5*iisize,"簇"+str(ii+1)) 57 ## 更新 y_lower 58 y_lower = y_upper + 5 59 ## 添加平均轮廓系数得分直线 60 plt.axvline(x=sil_score,color="red",label = "mean:"+str(np.round(sil_score,3))) 61 plt.xlim([-0.1,1]) 62 plt.yticks([]) 63 plt.legend(loc = 1) 64 plt.xlabel("轮廓系数得分") 65 plt.ylabel("聚类标签") 66 plt.title("K-medians聚类轮廓图") 67 plt.show()
2.层次聚类
2.1层次聚类(https://www.cnblogs.com/zongfa/p/9344769.html)
①原理
层次聚类(Hierarchical Clustering)是聚类算法的一种,通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树。在聚类树中,不同类别的原始数据点是树的最低层,树的顶层是一个聚类的根节点。创建聚类树有自下而上合并和自上而下分裂两种方法。
②算法流程
按照 层次分解是自下而上,还是自顶向下,层次的聚类方法可以进一步分为以下两种:
1)自下而上的 凝聚方法(agglomerative:先将所有样本的每个点都看成一个簇,然后找出距离最小的两个簇进行合并,不断重复到预期簇或者其他终止条件),
凝聚方法的代表算法:AGNES,Agglomerative Nesting
AGNES 算法步骤:
(1) 初始化,每个样本当做一个簇
(2) 计算任意两簇距离,找出 距离最近的两个簇,合并这两簇
(3) 重复步骤 (2)
直到,最远两簇距离超过阈值,或者簇的个数达到指定值,终止算法
2)自顶向下的 分裂方法(divisive:先将所有样本当作一整个簇,然后找出簇中距离最远的两个簇进行分裂,不断重复到预期簇或者其他终止条件)。
分裂方法的代表算法:DIANA,Divisive Analysis
DIANA 算法步骤:
(1) 初始化,所有样本集中归为一个簇
(2) 在同一个簇中,计算任意两个样本之间的距离,找到 距离最远 的两个样本点a,b,将 a,b 作为两个簇的中心;
(3) 计算原来簇中剩余样本点距离 a,b 的距离,距离哪个中心近,分配到哪个簇中
(4) 重复步骤(2)、(3)
直到,最远两簇距离不足阈值,或者簇的个数达到指定值,终止算法
③算法优缺点
层次算法算法的主要优点有:
1)距离和规则的相似度容易定义,限制少;
2)不需要预先制定聚类数;
3)可以发现类的层次关系;
4)可以聚类成其它形状
层次算法的主要缺点有:
1)计算复杂度太高;
2)奇异值也能产生很大影响;
3)算法很可能聚类成链状
④python代码
1)python实现

1 ## 层次聚类 2 ## 对数据进行系统聚类并绘制树 3 Z = hierarchy.linkage(tsne_wine_x, method="ward", metric="euclidean") 4 fig = plt.figure(figsize=(12,6)) 5 Irisdn = hierarchy.dendrogram(Z,truncate_mode = "lastp") 6 plt.axhline(y = 40,color="k",linestyle="solid",label="three class") 7 plt.axhline(y = 80,color="g",linestyle="dashdot",label="two class") 8 plt.title("层次聚类树") 9 plt.xlabel("Sample number") 10 plt.ylabel("距离") 11 plt.legend(loc = 1) 12 plt.show() 13 14 ## 计算系统聚类后每个簇的信息 15 ## 最多聚类为两类 16 hie2 = hierarchy.fcluster(Z,t = 2, criterion="maxclust") 17 print("聚为2个簇,每簇包含的样本数量:\n",np.unique(hie2,return_counts = True)) 18 print("聚为2个簇,聚类效果V测度: %.4f"%v_measure_score(wine_y,hie2)) 19 ## 最多聚类为三类 20 hie3 = hierarchy.fcluster(Z,t = 3, criterion="maxclust") 21 print("聚为3个簇,每簇包含的样本数量:\n",np.unique(hie3,return_counts = True)) 22 print("聚为3个簇,聚类效果V测度: %.4f"%v_measure_score(wine_y,hie3))
2)可视化

1 ## 将聚类为两类和3类的结果在空间中可视化出来 2 colors = ["red","blue","green"] 3 shapes = ["o","s","*"] 4 fig = plt.figure(figsize=(15,6)) 5 ## 将坐标系设置为3D,层次聚类结果 6 ax1 = fig.add_subplot(121, projection="3d") 7 for ii,y in enumerate(hie2-1): 8 ax1.scatter(tsne_wine_x[ii,0],tsne_wine_x[ii,1],tsne_wine_x[ii,2], 9 s = 40,c = colors[y],marker = shapes[y],alpha = 0.5) 10 ax1.set_xlabel("特征1",rotation=20) 11 ax1.set_ylabel("特征2",rotation=-20) 12 ax1.set_zlabel("特征3",rotation=90) 13 ax1.azim = 225 14 ax1.set_title("层次聚类为2簇") 15 16 ax2 = fig.add_subplot(122, projection="3d") 17 for ii,y in enumerate(hie3-1): 18 ax2.scatter(tsne_wine_x[ii,0],tsne_wine_x[ii,1],tsne_wine_x[ii,2], 19 s = 40,c = colors[y],marker = shapes[y],alpha = 0.5) 20 ax2.set_xlabel("特征1",rotation=20) 21 ax2.set_ylabel("特征2",rotation=-20) 22 ax2.set_zlabel("特征3",rotation=90) 23 ax2.azim = 225 24 ax2.set_title("层次聚类为3簇") 25 plt.tight_layout() 26 plt.show()
2.2谱聚类(https://www.cnblogs.com/pinard/p/6221564.html)
①原理
把所有的数据看做空间中的点,这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低,而距离较近的两个点之间的边权重值较高,通过对所有数据点组成的图进行切图,让切图后不同的子图间边权重和尽可能的低,而子图内的边权重和尽可能的高,从而达到聚类的目的。
②算法流程
输入:样本集D=(x1,x2,...,xn);相似矩阵的生成方式;降维后的维度k1;聚类方法;聚类后的维度k2
输出: 簇划分C(c1,c2,...ck2)
1) 根据输入的相似矩阵的生成方式构建样本的相似矩阵S
2)根据相似矩阵S构建邻接矩阵W,构建度矩阵D
3)计算出拉普拉斯矩阵L
4)构建标准化后的拉普拉斯矩阵D−1/2LD−1/2
5)计算D−1/2LD−1/2最小的k1个特征值所各自对应的特征向量f
6) 将各自对应的特征向量f组成的矩阵按行标准化,最终组成n×k1维的特征矩阵F
7)对F中的每一行作为一个k1维的样本,共n个样本,用输入的聚类方法进行聚类,聚类维数为k2。
8)得到簇划分C(c1,c2,...ck2)
③算法优缺点
谱聚类算法的主要优点有:
1)谱聚类只需要数据之间的相似度矩阵,因此对于处理稀疏数据的聚类很有效。这点传统聚类算法比如K-Means很难做到
2)由于使用了降维,因此在处理高维数据聚类时的复杂度比传统聚类算法好。
谱聚类算法的主要缺点有:
1)如果最终聚类的维度非常高,则由于降维的幅度不够,谱聚类的运行速度和最后的聚类效果均不好。
2) 聚类效果依赖于相似矩阵,不同的相似矩阵得到的最终聚类效果可能很不同。
④python代码
1)python实现

1 ## 使用K近邻算法相似矩阵的建立方式 2 speclu_nei = SpectralClustering(n_clusters=3, # 投影到子空间的维度 3 affinity="nearest_neighbors", # 相似矩阵的建立方式 4 n_neighbors = 5, # 相似矩阵的建立时使用的近邻数 5 random_state = 123) 6 speclu_nei.fit(tsne_wine_x) 7 ## 计算聚类的效果 8 nei_pre = speclu_nei.labels_ 9 print("聚为3个簇,每簇包含的样本数量:\n",np.unique(nei_pre,return_counts = True)) 10 print("聚为3个簇,聚类效果V测度: %.4f"%v_measure_score(wine_y,nei_pre)) 11 ## 使用rbf算法相似矩阵的建立方式 12 speclu_rbf = SpectralClustering(n_clusters=3, # 投影到子空间的维度 13 affinity="rbf", # 相似矩阵的建立方式 14 gamma = 0.005, # 相似矩阵的建立时使用的参数 15 random_state = 123) 16 speclu_rbf.fit(tsne_wine_x) 17 ## 计算聚类的效果 18 rbf_pre = speclu_rbf.labels_ 19 print("聚为3个簇,每簇包含的样本数量:\n",np.unique(rbf_pre,return_counts = True)) 20 print("聚为3个簇,聚类效果V测度: %.4f"%v_measure_score(wine_y,rbf_pre))
2)可视化

1 ## 可视化中不同的聚类结果构建的相似矩阵 2 plt.figure(figsize=(14,6)) 3 plt.subplot(1,2,1) 4 sns.heatmap(speclu_nei.affinity_matrix_.toarray(),cmap="YlGnBu") 5 plt.title("K近邻算法构建的相似矩阵") 6 plt.subplot(1,2,2) 7 sns.heatmap(speclu_rbf.affinity_matrix_,cmap="YlGnBu") 8 plt.title("RBF构建的相似矩阵") 9 plt.tight_layout() 10 plt.show() 11 12 ## 在二维空间中可视化两种不同的算法构建的节点网络 13 colors = ["red","blue","green"] 14 shapes = ["o","s","*"] 15 nei_mat = speclu_nei.affinity_matrix_.toarray() 16 rbf_mat = speclu_rbf.affinity_matrix_ 17 18 ## 可视化网络图 19 plt.figure(figsize=(14,6)) 20 ## 使用K近邻算法获得的网路图 21 plt.subplot(1,2,1) 22 G1 = nx.Graph(nei_mat) ## 生成无项图 23 pos1=graphviz_layout(G1,prog="fdp") 24 for ii in range(3): # 为每种类型的点设置颜色和形状 25 nodelist = np.arange(len(wine_y))[wine_y == ii] 26 nx.draw_networkx_nodes(G1,pos1,nodelist = nodelist,alpha=0.8, 27 node_size=50,node_color = colors[ii], 28 node_shape=shapes[ii]) 29 nx.draw_networkx_edges(G1,pos1,width=1,edge_color= "k") 30 plt.title("K近邻算法构建网络") 31 ## 使用RBF算法获得的网路图 32 plt.subplot(1,2,2) 33 G2 = nx.Graph(rbf_mat) ## 生成无项图 34 pos2=graphviz_layout(G2,prog="fdp") 35 for ii in range(3): # 为每种类型的点设置颜色和形状 36 nodelist = np.arange(len(wine_y))[wine_y == ii] 37 nx.draw_networkx_nodes(G2,pos2,nodelist = nodelist,alpha=0.8, 38 node_size=50,node_color = colors[ii], 39 node_shape=shapes[ii]) 40 nx.draw_networkx_edges(G2,pos2,width=1,alpha = 0.1,edge_color= "gray") 41 plt.title("RBF算法构建网络") 42 plt.tight_layout() 43 plt.show()
2.3BIRCH聚类算法(https://www.cnblogs.com/pinard/p/6179132.html)
①原理
通过扫描数据库,建立一个初始存放于内存中的聚类特征树,然后对聚类特征树的叶结点进行聚类。它的核心是聚类特征(CF)和聚类特征树(CF Tree)。
CF 树是一棵具有两个参数的高度平衡树,用来存储层次聚类的聚类特征。它涉及到两个参数分支因子和阈值。其中,分支因子B指定子节点的最大数目,即每个非叶节点可以拥有的孩子的最大数目。阈值T 指定存储在叶节点的子簇的最大直径,它影响着CF 树的大小。改变阈值可以改变树的大小。CF树是随着数据点的插入而动态创建的,因此该方法是增量的。
CF树的构造过程实际上是一个数据点的插入过程,其步骤为:
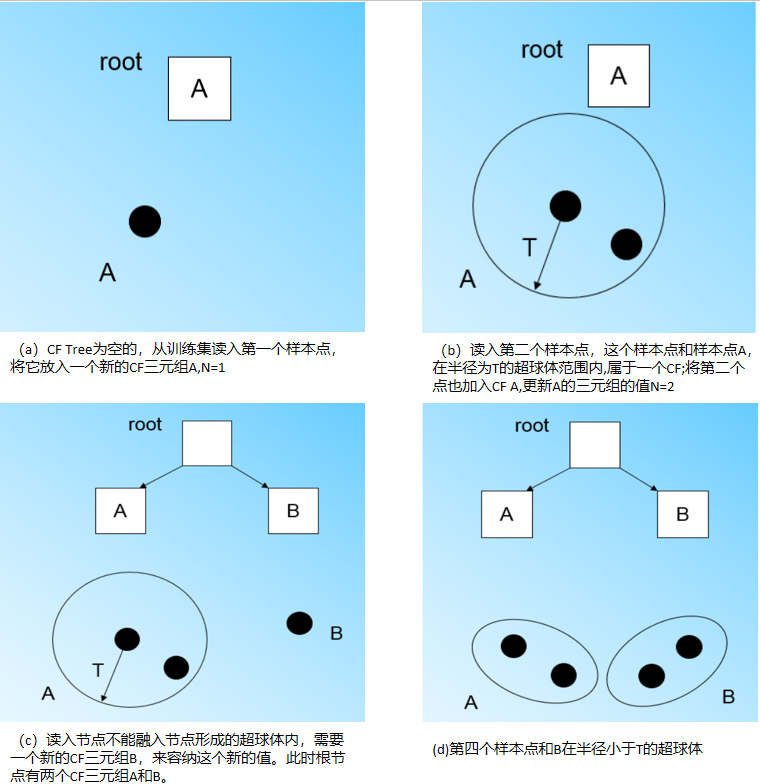
图3 CF tree生长过程
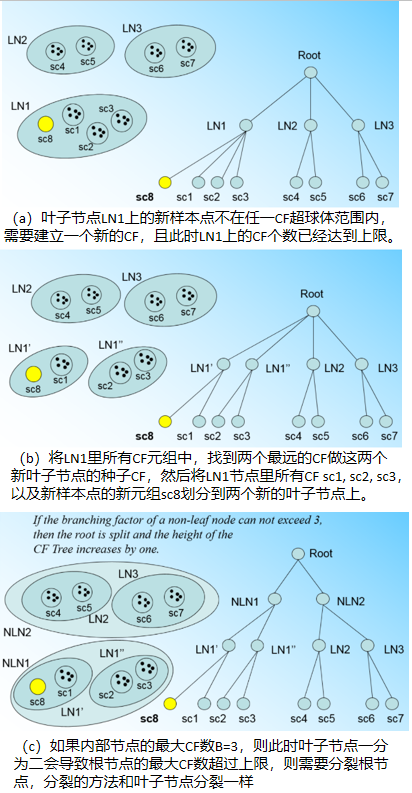
图4 CF tree分裂过程
②算法流程
1) 将所有的样本依次读入,在内存中建立一颗CF Tree。
2)对叶节点进一步利用一个全局性的聚类算法,改进聚类质量。 由于CF 树的叶节点代表的聚类可能不是自然的聚类结果,原因是给定的阈值限制了簇的大小,并且数据的输入顺序也会影响到聚类结果。因此,需要对叶节点进一步利用一个全 局性的聚类算法,改进聚类质量:
(可选)将第一步建立的CF Tree进行筛选,去除一些异常CF节点,这些节点一般里面的样本点很少。对于一些超球体距离非常近的元组进行合并。
(可选)利用其它的一些聚类算法比如K-Means对所有的CF元组进行聚类,得到一颗比较好的CF Tree.这一步的主要目的是消除由于样本读入顺序导致的不合理的树结构,以及一些由于节点CF个数限制导致的树结构分裂。
(可选)利用第三步生成的CF Tree的所有CF节点的质心,作为初始质心点,对所有的样本点按距离远近进行聚类。这样进一步减少了由于CF Tree的一些限制导致的聚类不合理的情况。
③算法优缺点
BIRCH算法的主要优点有:
1) 节约内存,所有的样本都在磁盘上,CF Tree仅仅存了CF节点和对应的指针。
2) 聚类速度快,只需要一遍扫描训练集就可以建立CF Tree,CF Tree的增删改都很快。
3) 可以识别噪音点,还可以对数据集进行初步分类的预处理。
BIRCH算法的主要缺点有:
1) 由于CF Tree对每个节点的CF个数有限制,导致聚类的结果可能和真实的类别分布不同。
2) 对高维特征的数据聚类效果不好。此时可以选择Mini Batch K-Means。
3) 如果数据集的分布簇不是类似于超球体,或者说不是凸的,则聚类效果不好。
④python代码
1)python实现

1 ## 计算聚为不同簇的V测度大小 2 vm = [] 3 n_cluster = 10 4 for cluster in range(1,n_cluster): 5 birch = Birch(threshold = 0.5, ## 合并样本的半径阈值 6 branching_factor = 20, ## 每个节点中CF子集群的最大数量 7 n_clusters=cluster) 8 birch.fit(tsne_wine_x) # 拟合模型 9 vm.append(v_measure_score(wine_y,birch.labels_)) 10 ## 可视化V测度的变化情况 11 plt.figure(figsize=(10,6)) 12 plt.plot(range(1,n_cluster),vm,"r-o") 13 plt.xlabel("聚类数目") 14 plt.ylabel("V测度") 15 plt.title("BIRCH聚类") 16 ## 在图中添加一个箭头 17 plt.annotate("V测度最高", xy=(3,vm[2]),xytext=(4,0.5), 18 arrowprops=dict(facecolor='blue', shrink=0.1)) 19 plt.grid() 20 plt.show() 21 22 ## 使用参数网格搜索的方法寻找最合适的threshold 和 ranching_factor参数 23 thre = [0.1,0.2,0.3,0.4,0.5, 0.75, 1,1.5,2,3,5] 24 ranch = np.arange(5,50,5) 25 threx, ranchy = np.meshgrid(thre,ranch) 26 vm = np.ones_like(threx) 27 ## 计算不同参数组合下的V测度 28 for i,t in enumerate(thre): 29 for j,r in enumerate(ranch): 30 birch = Birch(threshold = t,branching_factor = r, 31 n_clusters=3) 32 birch.fit(tsne_wine_x) # 拟合模型 33 vm[j,i] = (v_measure_score(wine_y,birch.labels_)) 34 35 36 ## 使用3D曲面图可视化交叉验证的平均均方根误差 37 ## 数据准备 38 x, y = np.meshgrid(range(len(thre)),range(len(ranch))) 39 ## 可视化 40 fig = plt.figure(figsize=(10,6)) 41 ax1 = fig.add_subplot(111, projection="3d") 42 surf = ax1.plot_surface(x,y,vm,cmap=plt.cm.coolwarm, 43 linewidth=0.1) 44 plt.xticks(range(len(thre)),thre,rotation=45) 45 plt.yticks(range(len(ranch)),ranch,rotation=125) 46 ax1.set_xlabel("threshold",labelpad=25) 47 ax1.set_ylabel("ranching_factor",labelpad=15) 48 ax1.set_zlabel("V测度",rotation = 90,labelpad=10) 49 plt.title("BIRCH参数搜索") 50 plt.tight_layout() 51 plt.show() 52 53 ## 可以发现,当threshold=2时,聚类效果较好 54 55 ## 使用合适的参数聚类为3类 56 birch = Birch(threshold = 2, ## 合并样本的半径阈值 57 branching_factor = 20, ## 每个节点中CF子集群的最大数量 58 n_clusters=3) 59 birch.fit(tsne_wine_x) # 拟合模型 60 print("BIRCH聚类,每簇包含的样本数量:",np.unique(birch.labels_,return_counts = True)) 61 print("聚类效果V测度: %.4f"%v_measure_score(wine_y,birch.labels_)) 62 63 ## 在3维空间中可视化聚类的效果 64 colors = ["red","blue","green"] 65 shapes = ["o","s","*"] 66 birch_pre = birch.labels_ 67 fig = plt.figure(figsize=(10,6)) 68 ## 将坐标系设置为3D,Birch模型聚类结果 69 ax1 = fig.add_subplot(111, projection="3d") 70 for ii,y in enumerate(birch_pre): 71 ax1.scatter(tsne_wine_x[ii,0],tsne_wine_x[ii,1],tsne_wine_x[ii,2], 72 s = 40,c = colors[y],marker = shapes[y],alpha = 0.5) 73 ax1.set_xlabel("特征1",rotation=20) 74 ax1.set_ylabel("特征2",rotation=-20) 75 ax1.set_zlabel("特征3",rotation=90) 76 ax1.azim = 225 77 ax1.set_title("BIRCH模型聚为3簇") 78 plt.tight_layout() 79 plt.show()
3.DBSCAN(https://www.cnblogs.com/pinard/p/6208966.html)
①原理
由密度可达关系导出的最大密度相连的样本集合,即为我们最终聚类的一个类别,或者说一个簇:任意选择一个没有类别的核心对象作为种子,然后找到所有这个核心对象能够密度可达的样本集合,即为一个聚类簇。接着继续选择另一个没有类别的核心对象去寻找密度可达的样本集合,这样就得到另一个聚类簇。一直运行到所有核心对象都有类别为止。
1) ϵ-邻域:对于xj∈D,其ϵ-邻域包含样本集D中与xj的距离不大于ϵ的子样本集,即Nϵ(xj)={xi∈D|distance(xi,xj)≤ϵ}, 这个子样本集的个数记为|Nϵ(xj)|
2) 核心对象:对于任一样本xj∈D,如果其ϵ-邻域对应的Nϵ(xj)至少包含MinPts个样本,即如果|Nϵ(xj)|≥MinPts,则xj是核心对象。
3)密度直达:如果xi位于xj的ϵ-邻域中,且xj是核心对象,则称xi由xj密度直达。注意反之不一定成立,即此时不能说xj由xixi密度直达, 除非且xi也是核心对象。
4)密度可达:对于xi和xj,如果存在样本样本序列p1,p2,...,pT,满足p1=xi,pT=xj, 且pt+1由pt密度直达,则称xj由xi密度可达。也就是说,密度可达满足传递性。此时序列中的传递样本p1,p2,...,pT均为核心对象,因为只有核心对象才能使其他样本密度直达。注意密度可达也不满足对称性,这个可以由密度直达的不对称性得出。
5)密度相连:对于xi和xj,如果存在核心对象样本xk,使xi和xj均由xk密度可达,则称xi和xj密度相连。注意密度相连关系是满足对称性的。
②算法流程
输入:样本集D=(x1,x2,...,xm),邻域参数(ϵ,MinPts)(ϵ,MinPts), 样本距离度量方式
输出: 簇划分C={C1,C2,...,Ck}
1)初始化核心对象集合Ω=∅, 初始化聚类簇数k=0,初始化未访问样本集合Γ = D, 簇划分C = ∅
2) 对于j=1,2,...m, 按下面的步骤找出所有的核心对象:
a) 通过距离度量方式,找到样本xjxj的ϵϵ-邻域子样本集Nϵ(xj)
b) 如果子样本集样本个数满足|Nϵ(xj)|≥MinPts,将样本xj加入核心对象样本集合:Ω=Ω∪{xj}
3)如果核心对象集合Ω=∅,则算法结束,否则转入步骤4.
4)在核心对象集合Ω中,随机选择一个核心对象o,初始化当前簇核心对象队列Ωcur={o}, 初始化类别序号k=k+1,初始化当前簇样本集合Ck={o}, 更新未访问样本集合Γ=Γ−{o}
5)如果当前簇核心对象队列Ωcur=∅,则当前聚类簇Ck生成完毕, 更新簇划分C={C1,C2,...,Ck}, 更新核心对象集合Ω=Ω−Ck, 转入步骤3。否则更新核心对象集合Ω=Ω−Ck。
6)在当前簇核心对象队列Ωcur中取出一个核心对象o′,通过邻域距离阈值ϵϵ找出所有的ϵ-邻域子样本集Nϵ(o′),令Δ=Nϵ(o′)∩Γ, 更新当前簇样本集合Ck=Ck∪Δ, 更新未访问样本集合Γ=Γ−Δ, 更新Ωcur=Ωcur∪(Δ∩Ω)−o′,转入步骤5.
③算法优缺点
DBSCAN的主要优点有:
1) 可以对任意形状的稠密数据集进行聚类,相对的,K-Means之类的聚类算法一般只适用于凸数据集。
2) 可以在聚类的同时发现异常点,对数据集中的异常点不敏感。
3) 聚类结果没有偏倚,相对的,K-Means之类的聚类算法初始值对聚类结果有很大影响。
DBSCAN的主要缺点有:
1)如果样本集的密度不均匀、聚类间距差相差很大时,聚类质量较差,这时用DBSCAN聚类一般不适合。
2) 如果样本集较大时,聚类收敛时间较长,此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。
3) 调参相对于传统的K-Means之类的聚类算法稍复杂,主要需要对距离阈值ϵϵ,邻域样本数阈值MinPts联合调参,不同的参数组合对最后的聚类效果有较大影响。
④python代码
1)数据输入

1 ## 密度聚类,使用双月数据集进行演示 2 moons = pd.read_csv("data/chap7/moonsdatas.csv") 3 print(moons.head()) 4 ## 可视化数据的分布情况 5 index0 = np.where(moons.Y == 0)[0] 6 index1 = np.where(moons.Y == 1)[0] 7 plt.figure(figsize=(10,6)) 8 plt.plot(moons.X1[index0],moons.X2[index0],"ro") 9 plt.plot(moons.X1[index1],moons.X2[index1],"bs") 10 plt.grid() 11 plt.title("数据分布情况") 12 plt.show()

#moonsdatas.csv内部数据 X1,X2,Y 0.7424200753567709,0.5855670971530897,0 1.7444393113646617,0.03909623608357027,1 1.6934790738838439,-0.19061851292737964,1 0.7395695138224223,0.6392745781975631,0 -0.37802468688813173,0.9748140740959461,0 0.8943965995923518,0.2684180118353568,0 -0.29963968538614105,0.8552920833977722,0 0.5990826764995416,0.8689869663938821,0 1.4487513724292789,-0.38561064828523417,1 0.9594990725132131,0.1961820698703347,0 -0.8997106712223975,0.06995877775187856,0 1.6675174947499802,-0.27512890687214797,1 0.40981132226076655,-0.3464058822185835,1 0.1783854555389263,-0.08150562888680847,1 -0.9903399229195686,0.07396486782342798,0 0.64143092786173,-0.422634014818711,1 0.6174911668832177,0.8624477557627027,0 0.9122707444030145,0.41976568984604457,0 1.8454853360335206,0.02427053731935118,1 -0.8517968147219294,0.3052569878189397,0 1.9571688666681026,0.10222186087128464,1 1.459200738327181,-0.3541572323460125,1 0.0568361751864634,0.634289329658039,1 0.345405711194895,-0.3374921582152528,1 0.10021502503213334,0.03682150898860592,1 -0.02372568458855653,0.9598729038394033,0 1.5484796677088024,-0.3088278792686746,1 -0.9725006638571696,0.2671843612455592,0 -0.07539756626085375,0.25782887433165075,1 0.6797041596628686,-0.3863258933020085,1 0.5563891498049013,0.7611245866283963,0 1.9066856045456826,0.048122673665592273,1 1.0852354070492092,-0.5157087439187823,1 -0.9751054318482008,0.13601296750396805,0 1.9927426654631033,0.1606651870176002,1 0.6296275380761032,-0.46359909951528167,1 1.7630873710175643,-0.09721359907943336,1 -0.2116591928235565,1.0518201595006507,0 0.9629940179504384,0.016291402851855586,0 0.9916078372712691,0.09002612207065792,0 -0.7681353789911676,0.5923980808743408,0 0.07132362547304566,1.030668868974684,0 -0.9632044040840658,0.13264710026354096,0 0.9586142482482164,0.508703368472232,0 0.24955673751082114,0.920982933645361,0 0.18341480774743935,-0.2381556496785117,1 0.8933985245017807,0.33605841632935957,0 0.4679447820744323,-0.36660931615987286,1 0.5376610250691192,-0.43421589741841754,1 0.7014993370434921,0.6848655710085387,0 0.9529500463705477,0.2354371899065051,0 0.25978521137508537,0.9933916276315788,0 1.8501332503342962,0.10449912393226825,1 0.4072671351869828,-0.1909447614554059,1 0.12060437594682927,0.9164623927178303,0 0.812548360472443,-0.390855503154816,1 0.4771417924580682,0.8714198709801048,0 0.9637022994364077,-0.5584406403890955,1 0.8836538231159422,0.5023518241189919,0 2.0783030591952203,0.3459281403976071,1 -0.3809581758248603,0.917332454888744,0 0.9136186796086495,0.15543255251652632,0 1.9419337152954537,0.5020559611408825,1 0.30571243003164894,-0.08341233284874061,1 0.8310084830370218,-0.4517011995275053,1 0.3322310441172739,0.8807485195212301,0 0.2223086157691117,0.8925137061203403,0 -0.9473502831485547,0.23507292797266616,0 0.8632606498577688,0.542845600632332,0 0.06085102961547313,1.003946878208531,0 0.42512522106272843,0.9055859472767139,0 -0.5577207459075265,0.8539267435503082,0 1.9786407791910676,0.3585702701370858,1 0.3980109762811974,0.9212561259849487,0 0.3324630347315997,1.0548029527351463,0 -0.972006657472121,0.32529289314727583,0 -0.46895298008644715,0.9222263865342955,0 0.6985336324278157,-0.46584479383396904,1 0.7531111873722609,0.5443503420204149,0 1.6039919379642473,-0.29165875992675616,1 1.5759923429948874,-0.2594985176566876,1 -0.9115970258502809,0.60810610041036,0 0.7791476535423524,-0.41921662949112987,1 0.3866717578799457,-0.1709939163384983,1 1.2844182774692592,-0.4068797394152577,1 1.9206183854828334,0.03853204975572547,1 0.0073481888336762845,0.48648145397506765,1 -0.7199301255711074,0.5337889943565324,0 0.2377901528422881,-0.14164841558781793,1 1.1347403988478986,-0.39891724559935565,1 -0.969753333647298,0.2309581548071133,0 0.6104078332585035,0.6177937325568452,0 -0.7167374064308867,0.6729053585387454,0 -0.8315305075029933,0.4104256046575462,0 1.9625369785177371,0.3143858104958859,1 0.965674899028712,0.23996433677016082,0 0.09541684177804129,0.9613966244651005,0 0.4122422820153855,0.9793532433620252,0 1.9611956712693253,0.19901792561154713,1 0.6279132573280283,0.8178082770163417,0 1.593481580531614,-0.2854862179994909,1 -0.5908333377389866,0.7832144794381733,0 1.8706205047559261,-0.16473066546427292,1 1.1325636767709943,-0.47146143089737447,1 0.014381269446944497,1.091541562294836,0 0.5961791643945252,-0.4011072294411995,1 0.09031798962222999,1.0280561659346794,0 1.951867165520074,0.09667582771033055,1 1.0037724696181787,0.09326458513382924,0 0.6011556615130206,0.8131531695132175,0 1.9297534152894598,0.3327809114416115,1 0.9275874084078487,-0.5007648288604377,1 0.9733979338940547,0.3044774570823104,0 0.06996217184930456,0.30713574181457837,1 -0.5785138518325845,0.7499917561004416,0 1.9525084457013187,0.28460210644257367,1 1.2064824526423523,-0.429515601914685,1 1.7516144289972853,-0.165532632105251,1 1.9572527009286234,0.4439072014321818,1 -1.062664750041987,-0.017496173860412606,0 0.0847243031008849,0.20096810440393123,1 -0.00642671967857226,0.5075440414332381,1 1.514383628049127,-0.39067455824398734,1 -0.09682184686039716,1.0579285080084353,0 -0.2016673552179985,0.9737924617675013,0 -0.9760218293641607,0.3534711547225126,0 0.9366443410624838,-0.4883766374172068,1 -0.46373197524171295,0.786166999540863,0 -0.8394063539792624,0.5764911847173955,0 0.140741041959623,0.20947589954563692,1 0.9684685005254524,0.033760825743885885,0 0.977075116764224,-0.5321723564983244,1 1.0956938441090138,-0.5036335514851537,1 1.834940672831108,-0.15718027215915625,1 -1.0235837649302866,0.2226638385321212,0 0.06946091823923636,0.12703908773736858,1 1.0141020743583369,-0.5205991269662286,1 0.13120637198442467,0.09314008542406058,1 0.7651064167933965,-0.5559036261549234,1 0.8893165693585728,0.4719883739173041,0 1.8444704814913961,0.1775486645392752,1 0.14451618387347567,1.0262395209796389,0 0.0502867760672027,0.35980378443531774,1 0.7423279172309605,0.5531455958946306,0 0.18387484959989897,-0.09781371243538876,1 -0.9599420744390267,0.0021819456552125784,0 -0.8384684659574201,0.41646329188388254,0 -0.23964389215786744,0.9390770021605571,0 -0.27937143094217826,1.010840130929605,0 1.924771844977743,0.44956006436557794,1 1.5342153163670667,-0.3025136003212331,1 -0.5750094527584974,0.6991559993348738,0 -0.3617069272031358,1.0646093552810245,0 0.03474985399505273,0.3517527458403409,1 -0.1406341424617487,1.0053183771518461,0 -0.5065830500860024,0.9088599893698406,0 0.10730842286882243,0.09893367668605536,1 0.2642861190571081,0.9535109099286527,0 -0.4928376895040211,0.7990606495292463,0 0.9343260660723371,0.16509792931824077,0 -0.24967549396941058,0.9728067668323792,0 0.7082200523222146,0.7393556226465736,0 -0.7965828148532713,0.5372735190814597,0 0.6501985591439242,0.7168393634110836,0 0.07233677803597276,0.2391725684576113,1 1.410245333970097,-0.5038786171210711,1 1.6876543793301135,-0.19029688196790173,1 -0.7297596529105603,0.7523248318784818,0 0.07370460592331096,0.21780604541311452,1 0.33998769643315424,-0.18515837453991976,1 1.963504058453493,0.43483847038169393,1 0.8029846890104163,-0.5009963724077396,1 -0.9855753482689671,0.14331946842933438,0 0.2932517488301456,-0.1138206535965404,1 1.23303152011868,-0.5483643166795109,1 1.3190621754867349,-0.5314246084870689,1 1.4666606133046796,-0.4240796210312127,1 0.03742372392427841,0.4252864902538817,1 0.40897423398862154,0.8450791721918022,0 -0.9412887494488528,0.39832822522454997,0 -0.9367502944876839,0.4866982206646459,0 0.9429897977773501,0.4475420907478511,0 0.03804337096858349,0.44080657254180833,1 0.15002781465586715,-0.03375298460737603,1 0.46700381267467844,-0.32040647736425354,1 -0.747349767238711,0.7710194556116463,0 0.08805449948896261,-0.03894138489214657,1 1.3818902356383433,-0.4246283535362205,1 0.7327132720759026,-0.5095956248857724,1 0.36500588944801615,-0.3690523825846015,1 1.8738052653275803,0.008991385747584416,1 0.02835283611048987,1.1252994163337442,0 0.7201526400664203,0.6454155823406507,0 1.6591501910116093,-0.17949652405908467,1 -0.6815353357484525,0.5724541629249003,0 1.0298516840179899,0.1457180666325067,0 0.44703354625506975,-0.33350708703343174,1 0.46708767255023714,-0.37266649386605766,1 1.217182371993511,-0.4691834237976201,1 -0.6668705564276686,0.7044687698434431,0
2)python实现

1 ## 对数据进行密度聚类,并可视化出聚类后的结果 2 epsdata = [0.2,0.2,0.13,1] ## 定义不同的eps参数的取值 3 min_sample = [5,10,5,10] ## 定义不同的min_samples参数的取值 4 plt.figure(figsize=(14,10)) 5 for ii,eps in enumerate(epsdata): 6 db = DBSCAN(eps=eps,min_samples = min_sample[ii]) 7 db.fit(moons[["X1","X2"]].values) 8 ## 获取聚类后的类别标签 9 db_pre_lab = db.labels_ 10 print("参数eps取值为:",eps,"参数min_samples取值为:",min_sample[ii]) 11 print("每簇包含的样本数量:",np.unique(db_pre_lab,return_counts = True)) 12 print("聚类效果V测度: %.4f"%v_measure_score(moons["Y"],db_pre_lab)) 13 print("============================") 14 ## 可视化出聚类后的结果 15 plt.subplot(2,2,ii+1) 16 sns.scatterplot(x=moons["X1"], y=moons["X2"], 17 style = db_pre_lab,s = 100) 18 plt.legend(loc = 1) 19 plt.grid() 20 plt.title("密度聚类:eps="+str(eps)+",min_samples="+str(min_sample[ii])) 21 plt.tight_layout() 22 plt.show() 23 24 ## 将密度聚类和Kmeans聚类的结果进行对比 25 ## 密度聚类 26 db = DBSCAN(eps=0.2,min_samples = 5) 27 db.fit(moons[["X1","X2"]].values) 28 db_pre_lab = db.labels_ 29 ## k均值聚类 30 km = KMeans(n_clusters=2,random_state=1) 31 k_pre = km.fit_predict(moons[["X1","X2"]].values) 32 ## 可视化两种算法的聚类效果 33 plt.figure(figsize=(14,6)) 34 plt.subplot(1,2,1) 35 sns.scatterplot(x=moons["X1"], y=moons["X2"], 36 style = db_pre_lab,s = 100) 37 plt.legend(loc = 1) 38 plt.grid() 39 plt.title("密度聚类") 40 plt.subplot(1,2,2) 41 sns.scatterplot(x=moons["X1"], y=moons["X2"], 42 style = k_pre,s = 100) 43 plt.legend(loc = 1) 44 plt.grid() 45 plt.title("Kmeans聚类") 46 plt.tight_layout() 47 plt.show()




 浙公网安备 33010602011771号
浙公网安备 33010602011771号