动态规划-01背包问题

动态规划简介

动态规划方法代表了这一类问题（最优子结构或者子问题最优性）的一般解法，是设计方法或者策略，不是具体算法。

动态规划的本质是递推，核心是找到状态转移的方式，写出dp方程，最利于解决重叠子问题（比如斐波那契方程）。

形式：

记忆型递归

递推

下面讲解下01背包问题：

问题描述：有n个重量和价值分别为wi，vi的物品，从这些物品中挑选出总重量不超过W的物品，求所有挑选方案中价值总和的最大值。

问题分析：使用dfs深度优先搜索，每次选择一个物品是否放进背包里，返回这两种选择中物品的最大价值。

直接dfs型代码如下：

int dfs(int * w,int * v,int number,int W,int n){
　　//退出判断条件
　　if(W <= 0) return 0;
　　if(n == number) return 0;
　　//不选第n个物品
　　int v1 = dfs(w,v,number,W,n+1);
　　//选择第n个物品
　　if(w[n] <= W){
　　　　int v2 = v[n]+dfs(w,v,number,W-w[n],n+1);
　　　　return v1>v2?v1:v2;
　　}else{
　　　　return v1;
　　}
}

记忆型递归型式：将之前已经计算过的值存储起来，简化后续步骤计算。

　　记忆型递归：递归之前判断，递归之后存储

代码如下：

/*记忆型递归*/
int dfs_memory(int* w,int* v,int number,int W,int n,int data[4][6]){
　　//退出判断条件
　　if(n == number) return 0;
　　if(W <= 0) return 0;
　　//递归之前判断
　　if(data[n][W] >= 0){
　　　　return data[n][W];
　　}
　　int value;
　　int v1 = dfs_memory(w,v,number,W,n+1,data);
　　if(w[n] <= W){
　　　　int v2 = v[n] + dfs_memory(w,v,number,W-w[n],n+1);
　　　　value = v1>v2?v1:v2;
　　}else{
　　　　value = v1;
　　}
　　//返回之前存储
　　data[n][W] = value;
　　cout << value << endl;
　　return value;
}

动态规划思路如下：

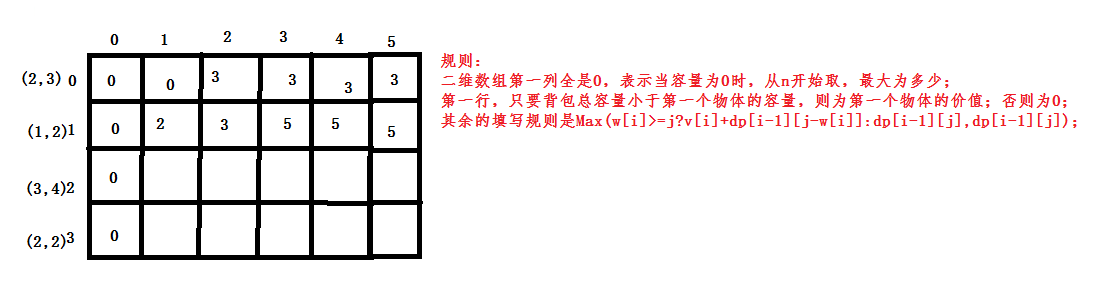
代码如下：

int dp(int* w,int* v,int number,int W){
　　int maxnum = 0;
　　int data[number][W+1];
　　//初始化data数组
　　for(int i = 0;i < number;i++){
　　　　data[i][0] = 0;
　　　　maxnum = Max(data[i][0],maxnum);
　　}
　　for(int i = 0;i < W+1;i++){
　　　　if(w[0] > i){
　　　　　　data[0][i] = 0;
　　　　}else{
　　　　　　data[0][i] = v[0];
　　　　}
　　　　maxnum = Max(data[0][i],maxnum);
　　}
　　//构造剩余data数组元素
　　for(int i = 1;i < number;i++){
　　　　for(int j = 1;j < W+1;j++){
　　　　　　data[i][j] = Max(w[i]<=j?v[i]+data[i-1][j-w[i]]:data[i-1][j],data[i-1][j]);
　　　　　　maxnum = Max(data[i][j],maxnum);
　　　　}
　　}
　　return maxnum;
}