【NOTE】Part 2

目录

• 坑（考前看）
  • • 下一个排列
    • 树的直径与重心
    • 单步容斥
    • 背包问题（链接忘记放了QAQ去日报找）
    • 一道题，开个坑，多重背包问题+单调队列优化
    • 二项式反演
    • *坑 斐波那契通项公式/状压枚举子集trick，二阶数列通项公式，数列前缀和，基本不等式
    • 错排问题
      • 解1：二项式反演
      • 解2：递推
    • 指数取模
    • \(P,NP,NPC\)问题
    • 菲薄内切数列通项公式及二阶递推式通项公式求法
      • 先说一阶递推。形如：
      • 然后是二阶递推式：
    • 我超，这也算点双
    • 我超，这个是边双

坑（考前看）

下一个排列

函数next_permutation(a+1,a+n+1)，且可用于可重排列

诶，不知道适不适合最后添加compare比较函数呢

具体的实现原理则是，两个相邻排列有着尽可能长的公共前缀。下降的排列不具有下一个排列。从后往前找到第一个不降的位置，再在这个位置后面寻找比其大的最小数，交换两者，最后令这个位置之后的序列升序排列。

---

树的直径与重心

幻想乡战略游戏（树剖解法）

吗的，怎么又看不懂，开坑了。

单步容斥

概念，合法方案=总方案-不合法方案。

背包问题（链接忘记放了QAQ去日报找）

似乎大多参考背包九讲。多人背包看得头疼（\(01\)背包\(k\)优解）。

一道题，开个坑，多重背包问题+单调队列优化

---

二项式反演

常用的几条柿饼：

\[(1)\ f_n=\sum\limits_{i=0}^n{n \choose i}g_i \iff g_n=\sum\limits_{i=0}^n(-1)^{n-i}{n \choose i}f_i \]

\[(2)\ f_n=\sum\limits_{i=m}^n{n \choose i}g_i \iff g_n=\sum\limits_{i=m}^n(-1)^{n-i}{n \choose i}f_i \]

\[(3)\ f_n=\sum\limits_{i=n}^m{i \choose n}g_i \iff g_n=\sum\limits_{i=n}^m(-1)^{i-n}{i \choose n}f_i \]

---

*坑 斐波那契通项公式/状压枚举子集trick，二阶数列通项公式，数列前缀和，基本不等式

---

错排问题

求\(n\)的全排列中每个元素都不在自己对应位置上的排列数。

解法通常两种，一种二项式反演（大家都说是容斥（）），一种是递推。

解1：二项式反演

\(p_i\)表示钦定\(i\)个元素在自己对应的位上的方案数，即

\[p_i={n \choose i} \]

再统计对应有重方案

\[f_i=(n-i)!p_i \]

又设\(g_i\)表示正好\(i\)个元素在自己对应位置上，则：

\[f_i=\sum\limits_{j=i}^n{j \choose i}g_j \]

由二项式反演：

\[g_i=\sum\limits_{j=i}^n(-1)^{j-i}{j \choose i}f_j \]

所求即为：

\[D_n=g_0=\sum\limits_{i=0}^n(-1)^if_i=n!\sum\limits_{i=0}^n(-1)^i\frac{1}{i!} \]

解2：递推

挺有意思的（

我们同样利用排列构造问题上，新加入一个元素\(i\)，考虑\(i\)与前面的数交换。但注意到：一个合法的错排并不一定是从另一个合法的错排通过这样的交换得来的。所以我们得这样考虑：如果将\(i\)放在\(k\)的位置...

1.如果将\(k\)放在\(i\)的位置，接下来就是\(n-2\)个数的错排问题。
2.如果\(k\)不放在\(i\)的位置，那么相当于有\(n-2\)个数不能放在自己位置上，\(k\)这个数不能放在\(i\)的位置上，所以是等价于\(n-1\)个数的错排问题。

由于\(k\)有\(i-1\)种取值，所以：

\[D_i=(i-1)(D_{i-1}+D_{i-2}) \]

---

指数取模

\[x^y \% p=x^{y\%\varphi(p)}\%p \]

特别地，\(p\)为质数的情况下，\(\varphi(p)=p-1\)：

\[x^y \% p=x^{y\%(p-1)}\%p \]

---

\(P,NP,NPC\)问题

似乎没有提及空间复杂度上的问题。

所以正常只需要判断，有多项式复杂度解的问题即为\(P\)问题，可以用多项式复杂度check解的问题即为\(NP\)问题。\(NPC\)问题是一种\(NP\)问题，但是不是一种\(P\)问题。任意\(NP\)问题都可以转化为\(NPC\)问题。

真 tm 神奇啊。

---

菲薄内切数列通项公式及二阶递推式通项公式求法

先说一阶递推。形如：

\[f_i=qf_{i-1}+p \]

高调里面有讲，就是构造

\[f_i+k=q(f_{i-1}+k) \]

然后数列\(\{a_i=f_i+k\}\)就会变成一个等比数列。得到：

\[\frac{a_i}{a_{i-1}}=q \]

再由累乘：

\[\begin{aligned} a_i&=\frac{a_i}{a_{i-1}}\cdot\frac{a_{i-1}}{a_{i-2}}\cdot\ \cdots\ \cdot\frac{a_2}{a_1}\cdot a_1 \\ &=a_1\cdot q^{i-1} \end{aligned} \]

这个\(k\)也很好球的，\(k=\frac{p}{q-1}\)。

最后得到

\[f_i=a_1 \cdot q^{i-1}-\frac{p}{q-1} \]

所得的通项公式是一个常数+等比的形式。

然后是二阶递推式：

\[f_i=af_{i-1}+bf_{i-2} \]

构造一对\(x,y\)，满足：

\[f_i-xf_{i-1}=y(f_{i-1}-xf_{i-2}) \]

同理又有：

\[f_i-yf_{i-1}=x(f_{i-1}-yf_{i-2}) \]

得

\[\left\{ \begin{aligned} a=x+y\\ b=-xy \end{aligned} \right. \]

又

\[x^2=ax+b \]

这就是特征方程，我到现在还没看懂是干啥的。继续看吧（

我们同样得到了一个比例关系：

\[\frac{f_i-xf_{i-1}}{f_{i-1}-xf_{i-2}}=y \]

与一阶递推同理地，有：

\[f_i-xf_{i-1}=y^{i-2}\times(f_2-xf_1) \]

同理又有：

\[f_i-yf_{i-1}=x^{i-2}\times(f_2-yf_1) \]

两柿相减得：

\[f_{i-1}=\frac{f_2-yf_1}{x-y}x^{i-2}+\frac{f_2-xf_1}{x-y}y^{i-2} \]

即：

\[f_{i}=\frac{f_2-yf_1}{x-y}x^{i-1}+\frac{f_2-xf_1}{x-y}y^{i-1} \]

写不动了。

---

我超，这也算点双

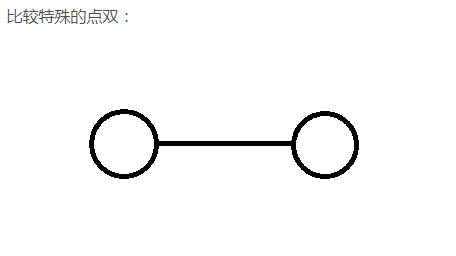
概念：

莫得割点。删去后图不连通的点叫割点

性质：

1. 除了上面这个特殊情况，点双连通图里任意两点之间有至少两条除了这两点之外无共同点的路径；

2. 一个割点包含于至少两个点双分量；

3. 非割点只包含于一个点双分量。

我超，这个是边双

概念：

莫得割边（桥）。删去后图不连通的边叫割边（桥）

性质：

1. 边双连通图里任意两点之间有至少两条无共同边的路径；

2. 边双分量里面可以存在割点；

3. 割边不属于任何边双分量。