CF954D Fight Against Traffic

传送门

---

这道题之所以是蓝题，是因为他的思路十分难想，但是代码很好写。

先理解一下题目:

在一个无向联通图上找到一条边，使得\(s \to t\)的最短路变小。

求这种边的个数。

---

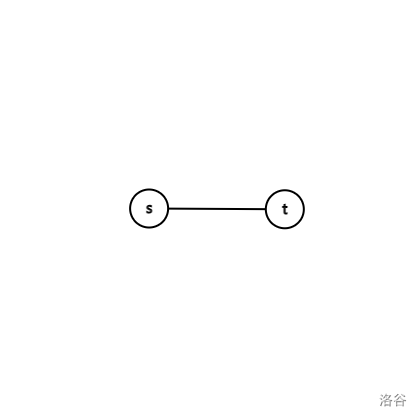
比如这个图，我们要使\(s \to t\)的距离变短，就得加一条边权为1的边\(x \to y\)。

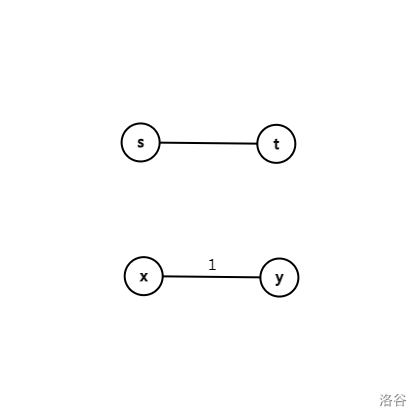
一共有两种路径可选

第一种：
\(s \to y \to x \to t\)

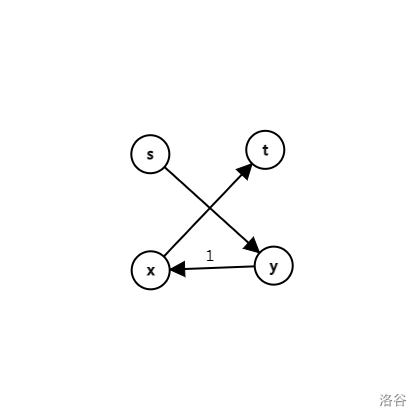
第二种：
\(s \to x \to y \to t\)

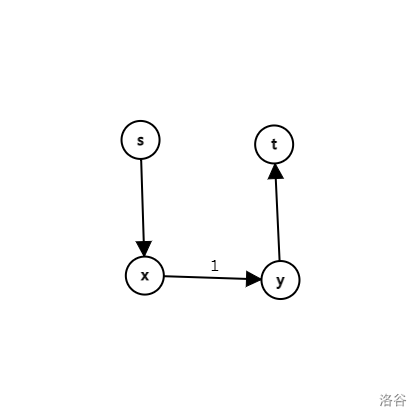
所以代码是这样实现的：

dis1[id]表示从s开始到id的最短路径。
dis2[id]表示从t开始到id的最短路径。

先从s和t分别做一遍dijkstra,他们的dis分别存在dis1和dis2里。

然后再\(O(n^2)\)找两个点(i, j)，表示(i, j)之间连了一条边，如果dis1[i] + dis2[j] + 1 >= dis1[t]即\(s \to x \to y \to t\)就说明加的这条边成功的让\(s \to t\)的最短路径变小了,ans++;

如果dis1[j] + dis2[i] + 1 >= dis1[t]即\(s \to y \to x \to t\)就说明加的这条边成功的也让\(s \to t\)的最短路径变小了,ans++;

还有一个细节，就是已经有的边就不能加了，所以用一个flag记录已经有的边，如果flag[i][j]就continue

代码：

#include <bits/stdc++.h>
using namespace std;
#define MAXN 1005
vector<int> myv[MAXN];
int dis1[MAXN], dis2[MAXN];
bool vis[MAXN];
bool flg[MAXN][MAXN];
void adde(int x, int y)
{
	myv[x].push_back(y);
}
void dijkstra(int s, int *dis)
{
	priority_queue<pair<int, int> > myq;
	memset(vis, 0, sizeof(vis));
	dis[s] = 0;
	myq.push(make_pair(0, s));
	while(!myq.empty())
	{
		int id = myq.top().second;
		int sum = myq.top().first;
		myq.pop();
		if(vis[id])
			continue;
		vis[id] = 1;
		for(int i = 0; i < myv[id].size(); i++)
		{
			int nxt = myv[id][i];
			if(dis[nxt] > dis[id] + 1)
			{
				dis[nxt] = dis[id] + 1;
				myq.push(make_pair(-dis[nxt], nxt));
			}
		}
	}
}
int main()
{
	int n, m, s, t;
	scanf("%d %d %d %d", &n, &m, &s, &t);
	for(int i = 1; i <= m; i++)
	{
		int u, v;
		scanf("%d %d", &u, &v);
		flg[u][v]=1;
		flg[v][u]=1;
		adde(u, v);
		adde(v, u);
	}
	memset(dis1, 0x3f, sizeof(dis1));
	dijkstra(s, dis1);
	memset(dis2, 0x3f, sizeof(dis2));
	dijkstra(t, dis2);
	int ans = 0;
	for(int i = 1; i <= n-1; i++)
	{
		for(int j = i+1; j <= n; j++)
		{	
			if(flg[i][j])
				continue;
			if(dis1[i]+dis2[j]+1 >= dis1[t] && dis1[j]+dis2[i]+1>=dis1[t])
			{
				ans++;
			}
		}
	}
	printf("%d\n", ans);
	return 0;
}