12306出票算法随想(一)
引言
每逢假日人流高峰,12306便会成为一个热门的话题,2016的春节也毫无例外。大年初二,我和汤雪华(NetFocus)一干人等,在QQ群里围绕12306的购票问题展开了热烈的讨论。最后,由于购票问题远比想象中复杂,所以最终还是公说公有理、婆说婆有理,没有得到一个较为清晰和明确的结果。于是决定动动笔,谈一谈自己的理解,重点是解决面对购票请求时能不能出票的问题。如果我的方法有漏洞,请一定指出,谢谢!
需要说明的是,我的离散数学和组合数学的知识,都早早地还给了我的体育老师,所以下面的这个算法可能会粗糙得让各位无法直视,只希望能完整地表达出我的想法。
出票规则臆测
由于已久未坐过火车,也从未在12306上买过票,所以我根据相关文章假想出以下的出票规则:
假设一列火车K110,从A始发,途经BCD三个站点,最终驶往终点E。那么旅客可以购买的将包括{AB, AC, AD, AE, BC, BD, BE, CD, CE, DE}这10种『区段』的客票。
假设列车承载限额为500人。如果有500名旅客购买了AE全程客票,之后无论哪个区间的客票,都不能再多卖一张了。如果有499名旅客购买了AE全程客票,那么还有的可能,一是再有人买到一张AE全程客票,使列车从始发到终点都满载;二是AE包含的AB/AC/AD/BC/BD/BE/CD/CE/DE每个区段都最多只能售出1张客票,此时就象先下后上原则,区段间彼此不能有交叉,前一个区段有人下车,后面的区段才能再有人上车。比如我们还可以同时出票1张AB,1张BC、1张CD和1张DE的组合,或者1张AC、1张CE的组合。反之,此时若同时有AC、BD、CD各出票1张,则列车到B站点时仍是满载,持BD者将无法上车,而到C站点时持AC者下车,故持CD者可上车。
正因如此,每当我们售出一张某个区段的客票,就会引发其他区段可售票数量产生相应变化。所以,即使是同一编号的列车,在不同日期出行班次内售出的客票总数,都会因为旅客购票区段、购票数量的不同而完全不一样。
在仔细观察后我发现,在列车从始发到终点的整个过程中,唯一不变的是列车最多能容纳的人数——『承载限额』。
承载限额
在此赘述『承载限额』的概念,是为了理清座位与车票之间的关系。
以我数年前坐火车的经历,如果列车还有空余座位,那么我们在购票后将得到一张打印了车厢号、座位号的车票。如果座位已经售罄,那么只要列车承载限额还在其负荷内,那么我们仍能购得一张车票,并凭此进站上车,尽管这张票只载明了车次,而无具体的车厢号与座位号。这便是『有座票』与『无座票』的由来。
由此衍生出的,售出的座号是否由系统回收后再行出售给后续区段旅客,成为干扰我们讨论的问题之一。而我当时假设系统不回收座号。即假设甲买到A到B的有座票,并且是最后一个座位:15车厢102号座。而乙随后买到B到D的票,系统并不因此将这个座位15-102再次出售给乙。而是当甲在B下车后,由车厢里没有座位的其他旅客自行占据使用。
经过讨论,我认识到纠结于是否回收实际的座号是个大大的错误。如果将无座号也视为一种虚拟的座位,那么对列车而言只需要区分满载与未满载两种情况:满载时不能再售票,未满载时可售后续区段的票。而整个列车所能承载的人数,或者说是负荷,都将始终是个常量。
在这样的设定下,能否出票的问题就变成了判断列车在特定的区段是否会超载的问题了。至于『有座票』与『无座票』,就自然退化为次要问题了。
至于高铁和动车,我还没有坐过,所以只能揣测由于其车载设备的同步能力远比现有火车强大,因此借由列车员或其他机制实现空闲座号回收与更新,应该不是难题。
总体思路
在我当初大学的《数据结构》课程里,曾经有一个关于银行排队的算法模拟,我的灵感便正得于此。
第一步
明确整个算法的前提:『任意时刻列车均不得超载——列车承载的旅客人数不得超过其预定的承载限额。』进而,我推导出购票算法的准则:『每出售一张票,都必须保证列车不会因此在实际运行时超载。』
第二步
采取TDD的方法去模拟列车的运行。通过遍历列车经过的每个站点,按照先下后下的原则,计算每个站点上下旅客的数量以及列车的承载人数。当承载人数超过承载限额时,即说明多卖了一些不该卖的票,导致列车超载。这样,我们就可以设定不同区段已售出客票数量的不同组合,再提交给这个模拟的列车运行测试程序,以检验该售票结果是否正确。
第三步
设计出购票算法,模拟客户的购票请求,得到不同的售票结果,再提交给上面的测试程序检验,确保购票算法能产生符合要求的、正确的售票结果。
第四步
对已经正确的算法进行优化,通过重构提高算法的运算效率、降低并发竞争的风险。
第五步
围绕座号分配与回收、解决退票等问题,丰富设计功能,进一步满足业务需求。
综上所述,我的思路实际是模仿迷宫问题的递归,大致可以表述如下:
当一条线路收到一个购票请求时,它会用该请求包含的拟购票数去试探,通过遍历所有站点的已出售票数,模拟列车运行时的旅客上下车情况,检查期间是否会发生超载的情况。如果不会因此产生超载,则说明可以同意该购票请求。否则无论是在哪个站点发生超载,都必须拒绝这个购票请求。
明确了算法准则,下面我就从第二步开始,逐步实现上述预定思路。
注:因为Scala的简洁高效,所以我选择了它。另一方面也是因为我最近正陶醉其中,日后也希望有时间用Scala来模拟12306的客票并发。不过我自知此处的代码粗陋不堪,甚至站点的到达时间和发车时间我都用
Float模拟了,因为我还不知道Scala里用什么表示C#里的Timespan。😅
为有益于讨论,我把C#的实现代码放在了文末,有需要的可以点击此处直接前往。
搭建出票结果的测试环境
分析购票问题,我得到这样一张简单的类图。其中忽略了订票中心可以同时处理多条线路,同一线路可以选择不同机车运行,以及前述的上车有无座位等实际情况。
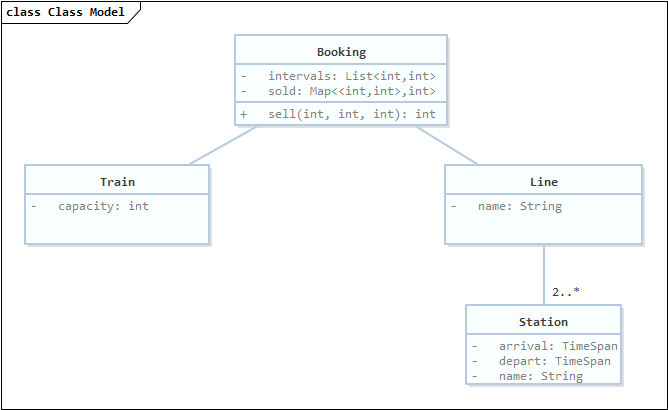
第一步:定义站点Station,线路Line
case class Station(val name: String, val arrival: Float, val depart: Float) {
require(arrival <= depart)
def before(that: Station): Boolean = this.depart < that.arrival
def after(that: Station): Boolean = this.arrival > that.depart
}
case class Line(val stations: List[Station]) {
require(stations.length >= 2)
}
第二步:定义列车Train
列车有2个很简单的方法:上客board与下客land,参数为上下车的人数。它们都会在超载时抛出异常。
class Train(val capacity: Int) {
var load: Int = 0
def land(amount: Int): Int = {
load -= amount
if (load < 0)
throw new IllegalArgumentException("Train loading should not be negative.")
amount
}
def board(amount: Int): Int = {
load += amount
if (load > capacity)
throw new IllegalArgumentException("Train is overloading.")
amount
}
}
第三步:定义订票中心Booking
订票中心是负责出票的地方。它先根据线路的站点列表生成一个包含所有区段的列表intervals,并将每个区段的已售票sold全部初始为0。这里,因为整数运算更快,所以我用了站点在Stations里的索引值,作为区段的两个端点值,即用(0,1)代替了(A,B)。之后我定义了一个售票方法sell(begin: Int, end: Int, amount: Int),它会简单地更新该区段已售票的数量。此外,还有两个函数beginWith与endWith,用来计算某个站点为始发或终点站时的上下车人数:下车的是所有以该站点为终点的客票总和,上车的是所有以该站点为起点的客票总和。
class Booking(val line: Line, val train: Train) {
val intervals: IndexedSeq[(Int, Int)] = line.stations.indices.dropRight(1).flatMap(
begin => ((begin + 1) until line.stations.length).map(
end => (begin, end)
)
)
val sold: mutable.Map[(Int, Int), Int] = intervals.map(i => i -> 0)(collection.breakOut)
def sell(begin: Int, end: Int, amount: Int) = {
require(begin < end)
sold(begin, end) += amount
}
def beginWith(station: Int): Int = {
var boarding = 0
for {
(begin, end) <- intervals
if begin == station
} boarding += sold(begin, end)
boarding
}
def endWith(station: Int): Int = {
var landing = 0
for {
(begin, end) <- intervals
if end == station
} landing += sold(begin, end)
landing
}
override def toString: String = {
(for ((begin, end) <- intervals)
yield s"${line.stations(begin).name}${line.stations(end).name}[${sold(begin, end)}]").mkString(" ")
}
}
第四步:定义测试驱动器Watcher
Watcher的核心方法是runTrain(),它模拟列车从始发站点出发,驶往终点。期间到达每个站点时,会模拟『先下后上』的原则,更新列车承载的旅客数量。
class Watcher(val booking: Booking) {
def runTrain() = {
for (
s <- booking.line.stations.indices
) {
print(s"Train arrived [${booking.line.stations(s).name}]: ")
printf("-[%3d] +[%3d] ", booking.train land booking.endWith(s), booking.train board booking.beginWith(s))
println(s"= ${booking.train.load} ")
}
}
}
第五步:让列车跑一会儿
最后,我模拟了一条线路line,包括有ABCDE一共5个站点;一列满载为100人的列车train;一个购票中心booking和模拟器watcher。然后在try-catch块里,我采取调用booking.sell(0, 1, 3)这样的方式,卖了5个区段的票,然后调用watch.runTrain()检验上述售票结果是否会超载。
object Railway {
def main(args: Array[String]) = {
val line = new Line(List(
Station("A", 1.0f, 1.0f),
Station("B", 2.0f, 2.1f),
Station("C", 3.0f, 3.1f),
Station("D", 4.0f, 4.2f),
Station("E", 5.0f, 5.0f)
))
val train = new Train(100)
val booking = new Booking(line, train)
val watcher = new Watcher(booking)
print("Line route[interval]: ")
print((for (s <- line.stations) yield s.name).mkString(" -> "))
println(s"\t[${booking.intervals.length}]")
try {
booking.sell(0, 1, 3)
booking.sell(0, 4, 30)
booking.sell(1, 2, 20)
booking.sell(1, 4, 35)
booking.sell(3, 4, 35)
println("Sold at this moment:")
println(booking)
watcher.runTrain()
} catch {
case e: IllegalArgumentException => println(e.getMessage)
}
}
}
运行程序,得到如下输出:
- 第一行是线路图,中括号里是包括的区段总数;
- 第二行是已售出的客票情况:区段[票数]
- 后面几行是模拟列车运行时上下旅客的情况:-[下车人数] +[上车人数] = 列车当前载客量
Line route[interval]: A -> B -> C -> D -> E [10]
Sold at this moment:
AB[3] AC[0] AD[0] AE[30] BC[20] BD[0] BE[35] CD[0] CE[0] DE[35]
Train arrived [A]: -[ 0] +[ 33] = 33
Train arrived [B]: -[ 3] +[ 55] = 85
Train arrived [C]: -[ 20] +[ 0] = 65
Train arrived [D]: -[ 0] +[ 35] = 100
Train arrived [E]: -[100] +[ 0] = 0
当我修改try中第二行为booking.sell(0, 4, 50)后,在B站点发生了超载而得到如下结果,证明了这样的售票结果是不正确的。
AB[3] AC[0] AD[0] AE[50] BC[20] BD[0] BE[35] CD[0] CE[0] DE[35]
Train arrived [A]: -[ 0] +[ 53] = 53
Train arrived [B]: Train is overloading.
实现购票算法
从上面的模拟,可以得到下面这样的一张图。图中每个结点对应一个站点,左叶代表在这个站点下车的人,右叶代表在这个站点上车的人。所有区段将会在左右各出现一次,分别对应区段的起点和终点。
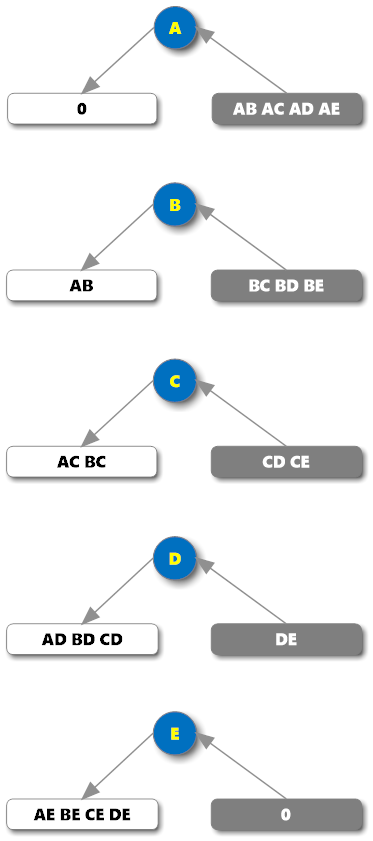
这一次,我先模拟了一组这样的已售客票:{AB[36] AC[4] AD[6] AE[32] BC[27] BD[0] BE[11] CD[0] CE[0] DE[12]}
booking.sell(0, 1, 36)
booking.sell(0, 2, 4)
booking.sell(0, 3, 6)
booking.sell(0, 4, 32)
booking.sell(1, 2, 27)
booking.sell(1, 4, 11)
booking.sell(3, 4, 12)
然后,利用上面的测试得到如下的上下旅客数据,证明这是一组有效的售票数据:
Train arrived [A]: -[ 0] +[ 78] = 78
Train arrived [B]: -[ 36] +[ 38] = 80
Train arrived [C]: -[ 31] +[ 0] = 49
Train arrived [D]: -[ 6] +[ 12] = 55
Train arrived [E]: -[ 55] +[ 0] = 0
接着,我开始为每个区段单独加入一条booking.sell,来测试该区段的最大可售票数量。比如下面这条,就是尝试AB段当前的最大可售票数量为22。
booking.sell(0, 1, 22)
最终,我得到了这样一张图,左边是每个站点上下旅客的情况,右边是对应该售票组合下,每个区段可供出售的最大票数。
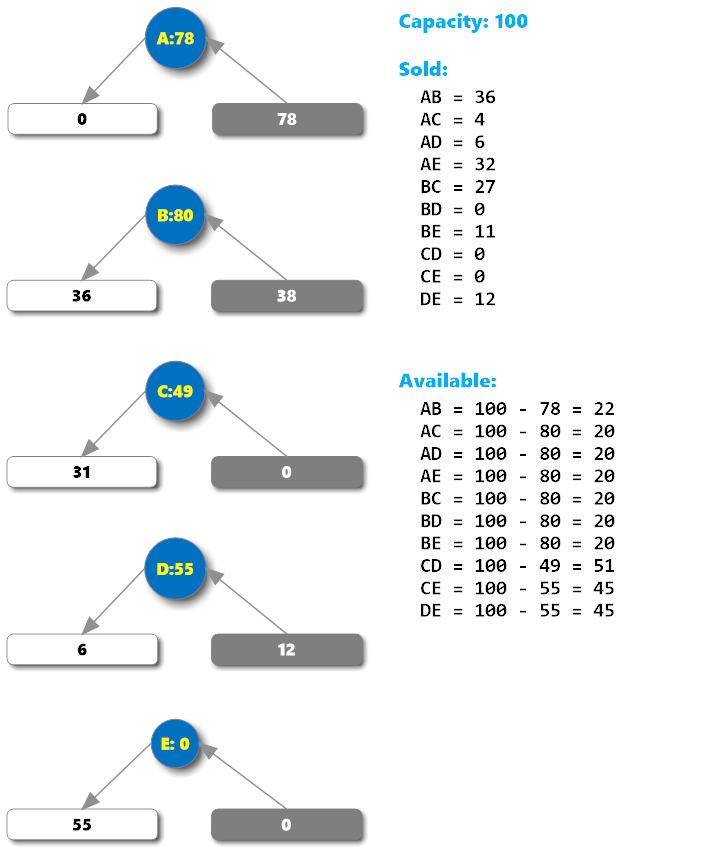
最大票数可以用这样一个公式表示之:available(x, y) = capacity - max(load(x) to load(y - 1)),即某个区间可售出的最大票数,等于列车的承载限额,与从始发站至终点前一站点间,各站点承载人数之最大值的差。(有点绕,看公式其实更直白 😝)
所以,我给booking添加了一个函数loadingAt,用来计算列车到达某个站点时的载客人数:
def loadingAt(station: Int): Int = station match {
case 0 => beginWith(station)
case _ => loadingAt(station - 1) - endWith(station) + beginWith(station)
}
再在此基础上,写出计算某个区段的最大待售票数的方法available
def available(begin: Int, end: Int): Int = {
require(begin < end)
train.capacity - (for {
station <- begin until end
} yield loadingAt(station)).max
}
最后,我们修改try,测试available函数是否正确可行
try {
booking.sell(0, 1, 36)
booking.sell(0, 2, 4)
booking.sell(0, 3, 6)
booking.sell(0, 4, 32)
booking.sell(1, 2, 27)
booking.sell(1, 4, 11)
booking.sell(3, 4, 12)
println("Sold at this moment:")
println(booking)
println("Available at this moment:")
println((for{(begin,end) <- booking.intervals
} yield {
s"${booking.line.stations(begin).name}${booking.line.stations(end).name}[${booking.available(begin,end)}]"
}).mkString(" "))
watcher.runTrain()
}
运行结果如下:
Line route[interval]: A -> B -> C -> D -> E [10]
Sold at this moment:
AB[36] AC[4] AD[6] AE[32] BC[27] BD[0] BE[11] CD[0] CE[0] DE[12]
Available at this moment:
AB[22] AC[20] AD[20] AE[20] BC[20] BD[20] BE[20] CD[51] CE[45] DE[45]
Train arrived [A]: -[ 0] +[ 78] = 78
Train arrived [B]: -[ 36] +[ 38] = 80
Train arrived [C]: -[ 31] +[ 0] = 49
Train arrived [D]: -[ 6] +[ 12] = 55
Train arrived [E]: -[ 55] +[ 0] = 0
可见available函数计算得到的数据,与上图中手工计算的结果是一致的,并且通过了runTrain的测试。
停下来再想一想
到这里,这个算法暂且是实现了。由于某个区段的可用票数,总是依赖于那一时刻已售出票数,所以该方法有两个主要特点:
- 无库存。各站点可用票不需要预先分配和设定
- 动态化。购票请求同意与否,在处理请求那一刻才由算法计算得出。
那么整个算法的瓶颈在哪里呢?显然是上面的递归loadingAt与available两个函数,其中有大量重复的加减运算。
其次是关于并发的处理。很显然,已售票数sold是整个计算发生竞争的核心,这从sold使用了mutable map即可见一斑,其他相关的计算也完全依赖于sold进行。所以,对sold的并发访问是解决并发竞争问题的关键。为此,优化loadingAt与available,减少占据sold的时间是第一步。进而可以将sold视为独占资源,将所有针对sold的请求排个队,按FIFO的原则依次处理。
暂作小节
本以为在一篇文章里就能实现所有的预期,但真动了笔才发现远没有那么轻松。所以,暂且以实现购票算法做为小节,把预留一定量的票、座位分配和并发访问等问题留待下一篇,甚至再下一篇,希望不至于因此烂尾。
作为对比,老汤在他的文章中用了一个很简单的出票方法,该方法的前提是『原子区间的可用票数,由工作人员在初始化车次时预先设定。』,即预先分配并设定每个区段的票数库存,然后每次接到购票请求时,就对每个区段的库存尝试减1。当所有区段库存减1的操作都能成功完成时,才能出票。
具体内容参见浅谈个人对12306的核心用户诉求的核心模型设计思路和架构设计
出票时扣减库存的逻辑是:根据订单信息,拿到出发地和目的地,然后获取这段区间里的所有的原子区间。然后尝试将每个原子区间的可用票数减1,如果所有的原子区间都够减,则购票成功;否则购票失败,提示用户该票已经卖完了。
最后,奉上C#的实现代码
using System;
using System.Collections.Generic;
using System.Diagnostics.Contracts;
using System.Linq;
namespace Ticket {
public static class Program {
public static void Main() {
var train = new Train(100);
var line = new Line(new List<Station> {
new Station("A", TimeSpan.Parse("1:00"), TimeSpan.Parse("1:00")),
new Station("B", TimeSpan.Parse("2:00"), TimeSpan.Parse("2:05")),
new Station("C", TimeSpan.Parse("3:00"), TimeSpan.Parse("3:10")),
new Station("D", TimeSpan.Parse("4:00"), TimeSpan.Parse("4:06")),
new Station("E", TimeSpan.Parse("5:00"), TimeSpan.Parse("5:00"))
});
var booking = new Booking(line, train);
var watcher = new Watcher(booking);
Console.Write("Line route[interval]: ");
foreach (var station in booking.Line.Stations)
Console.Write($"{station.Name} -> ");
Console.WriteLine($"[{booking.Intervals.Count}]");
try {
booking.Sell(0, 1, 36);
booking.Sell(0, 2, 4);
booking.Sell(0, 3, 6);
booking.Sell(0, 4, 32);
booking.Sell(1, 2, 27);
booking.Sell(1, 4, 11);
booking.Sell(3, 4, 12);
Console.WriteLine("Sold at this moment:");
Console.WriteLine(booking.ToString());
Console.WriteLine("Available at this moment:");
foreach (var interval in booking.Intervals) {
Console.Write(" {0}{1}[{2}]",
booking.Line.Stations[interval.Item1].Name,
booking.Line.Stations[interval.Item2].Name,
booking.Available(interval.Item1, interval.Item2));
}
Console.WriteLine();
watcher.RunTrain();
}
catch (ArgumentOutOfRangeException e) {
Console.WriteLine(e.Message);
}
}
}
internal class Station {
public Station(string name, TimeSpan arrival, TimeSpan depart) {
Contract.Requires(arrival <= depart);
Name = name;
Arrival = arrival;
Depart = depart;
}
public string Name { get; }
public TimeSpan Arrival { get; }
public TimeSpan Depart { get; }
public bool Before(Station that) => Depart < that.Arrival;
public bool After(Station that) => Arrival > that.Depart;
}
internal class Line {
public Line(IList<Station> stations) {
Contract.Requires(stations.Count >= 2);
Stations = stations;
}
public IList<Station> Stations { get; }
}
internal class Train {
public Train(int capacity) {
Contract.Requires(capacity > 0);
Capacity = capacity;
}
public int Capacity { get; }
public int Load { get; private set; }
public int Board(int amount) {
Load += amount;
if (Load > Capacity)
throw new ArgumentOutOfRangeException(nameof(amount), "Train is overloading.");
return amount;
}
public int Land(int amount) {
Load -= amount;
if (Load < 0)
throw new ArgumentOutOfRangeException(nameof(amount), "Train loading should not be negative.");
return amount;
}
}
internal class Booking {
public Booking(Line line, Train train) {
Line = line;
Train = train;
GenerateIntervals();
ResetSold();
}
public Line Line { get; }
public Train Train { get; }
public IList<Tuple<int, int>> Intervals { get; } = new List<Tuple<int, int>>();
private IDictionary<Tuple<int, int>, int> Sold { get; } = new Dictionary<Tuple<int, int>, int>();
public void Sell(int begin, int end, int amount) {
Contract.Requires(begin < end);
Contract.Requires(amount > 0);
var key = Sold.Keys.Single(k => k.Item1 == begin && k.Item2 == end);
Sold[key] += amount;
}
public int BeginWith(int station) => Sold.Where(p => p.Key.Item1 == station).Sum(v => v.Value);
public int EndWith(int station) => Sold.Where(p => p.Key.Item2 == station).Sum(v => v.Value);
private int LoadingAt(int station) {
switch (station) {
case 0:
return BeginWith(0);
default:
return LoadingAt(station - 1) - EndWith(station) + BeginWith(station);
}
}
public int Available(int begin, int end) {
Contract.Requires(begin < end);
var maxloading = 0;
for (var station = begin; station < end; station++)
maxloading = Math.Max(maxloading, LoadingAt(station));
return Train.Capacity - maxloading;
}
private void GenerateIntervals() {
Intervals.Clear();
for (var begin = 0; begin < Line.Stations.Count - 1; begin++) {
for (var end = begin + 1; end < Line.Stations.Count; end++)
Intervals.Add(new Tuple<int, int>(begin, end));
}
}
private void ResetSold() {
Sold.Clear();
foreach (var interval in Intervals)
Sold.Add(interval, 0);
}
public override string ToString() {
return Intervals.Aggregate(string.Empty, (current, interval) =>
current +
$" {Line.Stations[interval.Item1].Name}{Line.Stations[interval.Item2].Name}[{Sold[interval]}]");
}
}
internal class Watcher {
public Watcher(Booking booking) {
Booking = booking;
}
private Booking Booking { get; }
public void RunTrain() {
for (var station = 0; station < Booking.Line.Stations.Count; station++) {
Console.Write("Train arrived [{0}]:", Booking.Line.Stations[station].Name);
Console.WriteLine(" -{0,3}, +{1,3} = {2}",
Booking.Train.Land(Booking.EndWith(station)),
Booking.Train.Board(Booking.BeginWith(station)),
Booking.Train.Load);
}
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号