凸函数及其性质

上世纪70年代新的数学分支”凸分析”的出现，打破了分析数学中”线性”和”非线性”这样一个经典的却又是极不对称的分划格局，使得过去相当一部分非线性的内容(即”凸”内容)，能够象线性分析那样优美地得到高度统一的处理。一切理论和应用的非线性数学问题都朝着”凸”靠近，早已经构成数学和应用数学的重要思想。
由于凸函数是一类在优化问题中非常重要的函数，因此，其性质被广泛研究。而凸函数是定义在凸集上的。下面我们分别给出凸集与凸函数的定义与性质。

凸集、仿射集及其性质

凸集

定义： 设集合$C\subset {\mathbb{R}}^n$.若对$\mathrm{\forall }x,y\in C$,有

$$\theta x+(1-\theta )y\in C,\theta \in [0,1],$$

则称C为凸集。凸集的几何意义明显，即若x,y属于凸集，则其连线上所有的点都属于凸集C。凸集关于加法、数乘和交运算都是封闭的。即凸集之和为凸集、凸集的数乘为凸集、凸集相交为凸集

仿射集(affine set)

仿射集与凸集有一定类似。其关系类似于直线与线段的关系。（仿射集是开集，而凸集是闭集？）

凸函数的定义

凸函数的定义，是从凸集和优化的角度出发定义的。
定义：设集合$C$ 为非空凸集，函数$f:C\to \mathbb{R}$. 若对$\mathrm{\forall }x,y\in C$,有

$$f(tx+(1-t)y)\le tf(x)+(1-t)f(y)，t\in [0,1]$$

则称$f$为C上的凸函数。若不等式对$x\ne y$严格成立，则称$f$为$C$上的严格凸函数。
这个定义，可以如下理解，如下图所示的函数，是有极小点的。即凸函数的割线在函数曲线的上方。

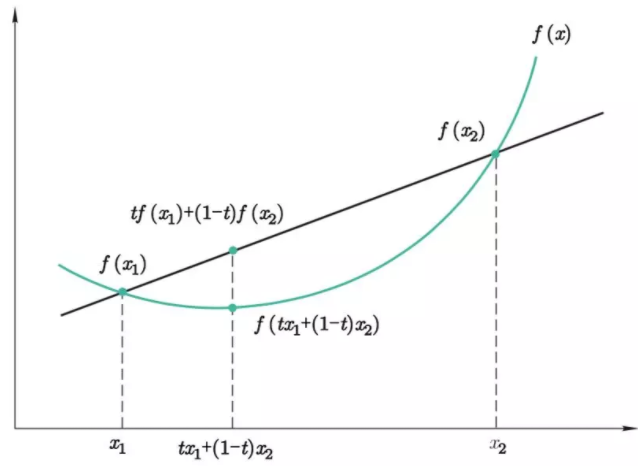
凸函数的判定

判断一个函数是否为凸函数，最基本的方法是使用其定义。但对可微函数，下面介绍的两个判定定理可能更为有效。

一阶判定条件

$f(x)$是凸函数，当且仅当对$\mathrm{\forall }x,y\in C$，有

$$f(y)\ge f(x)+g(x{)}^T(y-x)$$

二阶判定条件

对于一元函数，我们可以通过其二阶导数的符号来判断。如果函数的二阶导数总是非负，即，则是凸函数。
对于多元函数，我们可以通过其Hessian矩阵（Hessian矩阵是由多元函数的二阶导数组成的方阵）的正定性来判断。如果Hessian矩阵是半正定矩阵，则是凸函数。

凸函数的性质

• 设$f(x)$为定义在凸集S上的凸函数，则对任意非负数$c\ge 0$ ，函数$cf(x)$也是定义在凸集S上的凸函数。
• 设$f(x)$和$g(x)$都是定义在凸集S上的凸函数，则函数$f(x)+g(x)$也是定义在凸集S上的凸函数。
• 如果$f(x)$和$g(x)$都是定义在凸集S上的凸函数，且g递增，那么$h(x)=g(f(x))$是凸函数
• 设$f(x)$为定义在凸集S上的凸函数，则对任意实数c，集合$S_c=\{x|x\in S,f(x)\le c\}$是凸集。
• 设$f(x)$为定义在凸集上的凸函数，则它的任一个极小点就是它在S上的全局极小点，而且所有极小点的集合是凸集。

常见的凸函数