插入排序

插入排序跟打扑克牌一样，每次抽一张牌，按照从小到大的顺序插入到手里的正确位置，操作过程如下：

• 你从桌面上拿起第一张牌（已经排序）。
• 拿起第二张牌，插入到正确的位置。
• 拿起第三张牌，找到它应该在手中的位置，插入。
• 依次遍历每张牌，找到合适的位置插入。

速记口诀如下：左边有序，右边待插，拿起一张，插入应当

• "左边有序"：已排序部分，初始时只有第一个元素。
• "右边待插"：未排序部分，我们逐个取出元素。
• "拿起一张"：从未排序部分取一个数。
• "插入应当"：在有序部分找到合适的位置插入(即第一个比当前元素小的数的右侧)。

例如我们有一组数字：｛5，2，4，6，1，3｝，我们要将这组数字从小到大进行排列。

先假设有序列表中只有第1个元素，然后从第二个数字开始，将其认为是新增加的数字，这样第二个数字只需与其左边的第一个数字比较后排好序；

第三个数字时，只需与前两个数字比较即可；

以此类推，直到最后一个数字与前面的所有数字比较结束，插入排序完成。

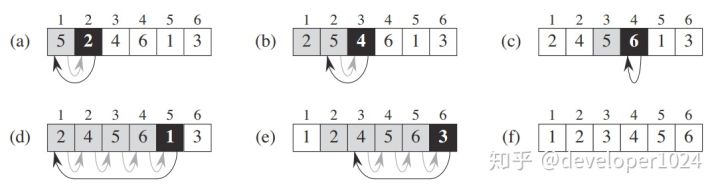
实现步骤：

1️⃣ 假设第 1 个元素是有序的，因此从 第 2 个元素（下标 1）开始排序。
2️⃣ 正向遍历未排序的元素列表，对于每个元素：

• 反向遍历已排序部分，找到第一个（即从左往右的第1个）比当前元素大的数。
• 比当前元素大的数都向右移动 1 位，腾出插入位置。

3️⃣ 插入位置：反向查找结束后 j + 1 的位置（即第一个比当前元素小的数的右侧）。

代码实现：

        const arr = [5,2,4,6,1,3];
        const len = arr.length;
        //假设第1个是有序的，因此只需从第2个（即下标为1的位置开始排序）元素开始进行排序
        for(let i=1;i<len;i++){
            const current = arr[i];
            let j = i - 1;
            //当前元素之前的都是有序表，在有序列表中，从后往前找到比当前元素大的第一个数
            while(j>=0 && arr[j] > current){
                //该排好序的数字向右移动1位(相当于当前j的地方让出了位置)
                arr[j+1] = arr[j];
                j--;
            }
            //原来j所在的位置设置为当前值：(因为原来找到了j的位置后，j--,因此这里需要+1，才能得到原有的位置)
            arr[j+1] = current;
        }
        console.log(arr);

 

 上述代码存在一个缺点，新插入的元素要按顺序依次往前查找，数据量较大时，必然比较耗时。改进方法是采用二分查找法

过程如下：

• 假设第一个元素是已经排好序的

• 从第二个元素开始，逐个处理：遍历未排序部分的元素，对于每个元素，我们用二分查找来 快速找到插入位置。

• 使用二分查找查找插入位置在已排序部分 arr[0...i-1] 中找到一个位置，这个位置满足：
  arr[position] <= current < arr[position + 1]（position 是当前元素 current 应该插入的合适位置）。

• 将找到位置后的元素向右移动
  
  • 通过二分查找，我们已经知道 current 应该插入的位置 left。
  • 接下来，我们需要将 所有大于 current 的元素向右移动一位，为 current 腾出位置。
  • 从 i - 1 到 left，我们 将这些元素都右移 1 位。
• 将 current 插入正确的位置
  最后，我们将 current 插入到 arr[left]

function binaryInsertionSort(arr) {
    const len = arr.length;

    for (let i = 1; i < len; i++) {
        let current = arr[i];
        let left = 0, right = i - 1;

        // ✅ 用二分查找找到插入位置
        while (left <= right) {
            let mid = Math.floor((left + right) / 2);
            if (arr[mid] > current) {
                right = mid - 1;  // 插入位置在左侧
            } else {
                left = mid + 1;   // 插入位置在右侧
            }
        }

        // ✅ 把 [left, i-1] 范围的元素整体向右移动 1 位
        for (let j = i - 1; j >= left; j--) {
            arr[j + 1] = arr[j];
        }

        // ✅ 在 left 位置插入 current
        arr[left] = current;
    }
    
    return arr;
}

// 测试
console.log(binaryInsertionSort([5, 2, 4, 6, 1, 3]));