11.26自顶向下 DFS
11/26
671. 二叉树中第二小的节点
思路:没写出来。
自己的代码:以为根节点的子节点中较大的一个就是答案。
class Solution { public: int findSecondMinimumValue(TreeNode* root) { stack<TreeNode*> st; if(!root) return -1; int minVal = root->val; st.push(root); TreeNode* node; while(!st.empty()){ node = st.top(); st.pop(); if(node->val > minVal) return node->val; if(node->left) st.push(node->left); if(node->right) st.push(node->right); } return -1; } };
可以发现:当次小的值可能藏在最底下,因此需要遍历整个树。
DFS
- 记录根节点的值(即最小值);定义第二小的数为-1。
- 对二叉树进行深度优先搜索(DFS),大于根节点值,并且小于第二小的数。
- 如果找到,则输出该值;如果找不到,则输出 -1。
lambda函数版
class Solution {
public:
int findSecondMinimumValue(TreeNode* root) {
if (!root || !root->left) return -1;
int minVal = root->val, secondMin = -1;
auto dfs = [&](auto &&dfs, TreeNode *node) { // lambda函数
if (!node) return;
if (node->val > minVal && (secondMin == -1 || node->val < secondMin))
secondMin = node->val; // 更新第二个数
dfs(dfs, node->left), dfs(dfs, node->right);
};
dfs(dfs, root);
return secondMin;
}
};
常规回溯函数版
class Solution {
int minVal , secondMin = -1;
void traversal(TreeNode* node){
if(!node) return;
if(node->val > minVal && (secondMin == -1 || node->val < secondMin)) secondMin = node->val;
traversal(node->left);
traversal(node->right);
}
public:
int findSecondMinimumValue(TreeNode* root) {
minVal = root->val;
traversal(root);
return secondMin;
}
};
补充知识:lambda函数
什么是 Lambda表达式
Lambda表达式是一种在被调用的位置或作为参数传递给函数的位置定义匿名函数对象(闭包)的简便方法。Lambda表达式的基本语法如下:
[capture list] (parameter list) -> return type { function body }
其中:
capture list是捕获列表,用于指定 Lambda表达式可以访问的外部变量,以及是按值还是按引用的方式访问。捕获列表可以为空,表示不访问任何外部变量,也可以使用默认捕获模式&或=来表示按引用或按值捕获所有外部变量,还可以混合使用具体的变量名和默认捕获模式来指定不同的捕获方式。parameter list是参数列表,用于表示 Lambda表达式的参数,可以为空,表示没有参数,也可以和普通函数一样指定参数的类型和名称,还可以在 c++14 中使用auto关键字来实现泛型参数。return type是返回值类型,用于指定 Lambda表达式的返回值类型,可以省略,表示由编译器根据函数体推导,也可以使用->符号显式指定,还可以在 c++14 中使用auto关键字来实现泛型返回值。function body是函数体,用于表示 Lambda表达式的具体逻辑,可以是一条语句,也可以是多条语句,还可以在 c++14 中使用constexpr来实现编译期计算。
Lambda表达式的捕获方式
-
值捕获(capture by value):在捕获列表中使用变量名,表示将该变量的值拷贝到 Lambda 表达式中,作为一个数据成员。值捕获的变量在 Lambda 表达式定义时就已经确定,不会随着外部变量的变化而变化。值捕获的变量默认不能在 Lambda 表达式中修改,除非使用
mutable关键字。例如:int x = 10; auto f = [x] (int y) -> int { return x + y; }; // 值捕获 x x = 20; // 修改外部的 x cout << f(5) << endl; // 输出 15,不受外部 x 的影响 -
引用捕获(capture by reference):在捕获列表中使用
&加变量名,表示将该变量的引用传递到 Lambda 表达式中,作为一个数据成员。引用捕获的变量在 Lambda 表达式调用时才确定,会随着外部变量的变化而变化。引用捕获的变量可以在 Lambda 表达式中修改,但要注意生命周期的问题,避免悬空引用的出现。例如:int x = 10; auto f = [&x] (int y) -> int { return x + y; }; // 引用捕获 x x = 20; // 修改外部的 x cout << f(5) << endl; // 输出 25,受外部 x 的影响 -
隐式捕获(implicit capture):在捕获列表中使用
=或&,表示按值或按引用捕获 Lambda 表达式中使用的所有外部变量。这种方式可以简化捕获列表的书写,避免过长或遗漏。隐式捕获可以和显式捕获混合使用,但不能和同类型的显式捕获一起使用。例如:int x = 10; int y = 20; auto f = [=, &y] (int z) -> int { return x + y + z; }; // 隐式按值捕获 x,显式按引用捕获 y x = 30; // 修改外部的 x y = 40; // 修改外部的 y cout << f(5) << endl; // 输出 55,不受外部 x 的影响,受外部 y 的影响 -
初始化捕获(init capture):C++14 引入的一种新的捕获方式,它允许在捕获列表中使用初始化表达式,从而在捕获列表中创建并初始化一个新的变量,而不是捕获一个已存在的变量。这种方式可以使用
auto关键字来推导类型,也可以显式指定类型。这种方式可以用来捕获只移动的变量,或者捕获this指针的值。例如:int x = 10; auto f = [z = x + 5] (int y) -> int { return z + y; }; // 初始化捕获 z,相当于值捕获 x + 5 x = 20; // 修改外部的 x cout << f(5) << endl; // 输出 20,不受外部 x 的影响
Lambda表达式的优点
Lambda表达式相比于普通函数和普通类,有以下几个优点:
- 简洁:Lambda表达式可以省略函数名和类名,直接定义和使用,使得代码更加简洁和清晰。
- 灵活:Lambda表达式可以捕获外部变量,可以作为函数参数,也可以作为函数返回值,使得代码更加灵活和方便。
- 安全:Lambda表达式可以控制外部变量的访问方式,可以避免全局变量的定义,可以避免悬空指针和无效引用的产生,使得代码更加安全和稳定。
Lambda表达式的示例
下面我们通过一些示例来展示 Lambda表达式的用法和效果。
示例一:使用 Lambda表达式定义简单的匿名函数
我们可以使用 Lambda表达式来定义一些简单的匿名函数,例如计算两个数的和、判断一个数是否为奇数等。例如:
#include <iostream>
using namespace std;
int main()
{
// 定义一个 Lambda表达式,计算两个数的和
auto plus = [] (int a, int b) -> int { return a + b; };
// 调用 Lambda表达式
cout << plus(3, 4) << endl; // 输出 7
// 定义一个 Lambda表达式,判断一个数是否为奇数
auto is_odd = [] (int n) { return n % 2 == 1; };
// 调用 Lambda表达式
cout << is_odd(5) << endl; // 输出 1
cout << is_odd(6) << endl; // 输出 0
return 0;
}
示例二:使用 Lambda表达式捕获外部变量
我们可以使用 Lambda表达式的捕获列表来指定 Lambda表达式可以访问的外部变量,以及是按值还是按引用的方式访问。例如:
#include <iostream>
using namespace std;
int main()
{
int x = 10;
int y = 20;
// 定义一个 Lambda表达式,按值捕获 x 和 y
auto add = [x, y] () -> int { return x + y; };
// 调用 Lambda表达式
cout << add() << endl; // 输出 30
// 修改 x 和 y 的值
x = 100;
y = 200;
// 再次调用 Lambda表达式
cout << add() << endl; // 输出 30,捕获的是 x 和 y 的副本,不受外部变化的影响
// 定义一个 Lambda表达式,按引用捕获 x 和 y
auto mul = [&x, &y] () -> int { return x * y; };
// 调用 Lambda表达式
cout << mul() << endl; // 输出 20000
// 修改 x 和 y 的值
x = 1000;
y = 2000;
// 再次调用 Lambda表达式
cout << mul() << endl; // 输出 2000000,捕获的是 x 和 y 的引用,会反映外部变化的影响
return 0;
}
示例三:使用 Lambda表达式作为函数参数
我们可以使用 Lambda表达式作为函数的参数,这样可以方便地定义和传递一些简单的函数对象,例如自定义排序规则、自定义比较函数等。例如:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// 定义一个结构体
struct Item
{
Item(int aa, int bb) : a(aa), b(bb) {}
int a;
int b;
};
int main()
{
vector<Item> vec;
vec.push_back(Item(1, 19));
vec.push_back(Item(10, 3));
vec.push_back(Item(3, 7));
vec.push_back(Item(8, 12));
vec.push_back(Item(2, 1));
// 使用 Lambda表达式,根据 Item 中的成员 a 升序排序
sort(vec.begin(), vec.end(), [] (const Item& v1, const Item& v2) { return v1.a < v2.a; });
// 使用 Lambda表达式,打印 vec 中的 Item 成员
for_each(vec.begin(), vec.end(), [] (const Item& item) { cout << item.a << " " << item.b << endl; });
return 0;
}
示例四:使用 Lambda表达式作为函数返回值
我们可以使用 Lambda表达式作为函数的返回值,这样可以方便地定义和返回一些简单的函数对象,例如工厂函数、闭包函数等。例如:
#include <iostream>
using namespace std;
// 定义一个函数,返回一个 Lambda表达式,实现两个数的加法
auto make_adder(int x)
{
return [x] (int y) -> int { return x + y; };
}
int main()
{
// 调用函数,得到一个 Lambda表达式
auto add5 = make_adder(5);
// 调用 Lambda表达式
cout << add5(10) << endl; // 输出 15
return 0;
}
Lambda表达式与普通函数和普通类的关系
Lambda表达式虽然是一种语法糖,但它本质上也是一种函数对象,也就是重载了 operator() 的类的对象。每一个 Lambda表达式都对应一个唯一的匿名类,这个类的名称由编译器自动生成,因此我们无法直接获取或使用。Lambda表达式的捕获列表实际上是匿名类的数据成员,Lambda表达式的参数列表和返回值类型实际上是匿名类的 operator() 的参数列表和返回值类型,Lambda表达式的函数体实际上是匿名类的 operator() 的函数体。例如,下面的 Lambda表达式:
int x = 10;
auto f = [x] (int y) -> int { return x + y; };
相当于定义了一个匿名类,类似于:
int x = 10;
class __lambda_1
{
public:
__lambda_1(int x) : __x(x) {} // 构造函数,用于初始化捕获的变量
int operator() (int y) const // 重载的 operator(),用于调用 Lambda表达式
{
return __x + y; // 函数体,与 Lambda表达式的函数体相同
}
private:
int __x; // 数据成员,用于存储捕获的变量
};
auto f = __lambda_1(x); // 创建一个匿名类的对象,相当于 Lambda表达式
由于 Lambda表达式是一种函数对象,因此它可以赋值给一个合适的函数指针或函数引用,也可以作为模板参数传递给一个泛型函数或类。例如:
#include <iostream>
using namespace std;
// 定义一个函数指针类型
typedef int (*func_ptr) (int, int);
// 定义一个函数,接受一个函数指针作为参数
void apply(func_ptr f, int a, int b)
{
cout << f(a, b) << endl;
}
int main()
{
// 定义一个 Lambda表达式,计算两个数的乘积
auto mul = [] (int x, int y) -> int { return x * y; };
// 将 Lambda表达式赋值给一个函数指针
func_ptr fp = mul;
// 调用函数,传递函数指针
apply(fp, 3, 4); // 输出 12
return 0;
}
C++14 和 C++17 对 Lambda表达式的扩展和改进
C++14 和 C++17 对 Lambda表达式进行了一些扩展和改进,使得 Lambda表达式更加强大和灵活。主要有以下几个方面:
- 泛型 Lambda:C++14 允许在 Lambda表达式的参数列表和返回值类型中使用
auto关键字,从而实现泛型 Lambda,即可以接受任意类型的参数和返回任意类型的值的 Lambda表达式。例如:
#include <iostream>
using namespace std;
int main()
{
// 定义一个泛型 Lambda,根据参数的类型返回不同的值
auto f = [] (auto x) -> auto
{
if (is_integral<decltype(x)>::value) // 如果 x 是整数类型
{
return x * 2; // 返回 x 的两倍
}
else if (is_floating_point<decltype(x)>::value) // 如果 x 是浮点类型
{
return x / 2; // 返回 x 的一半
}
else // 其他类型
{
return x; // 返回 x 本身
}
};
// 调用泛型 Lambda
cout << f(10) << endl; // 输出 20
cout << f(3.14) << endl; // 输出 1.57
cout << f("hello") << endl; // 输出 hello
return 0;
}
- 初始化捕获:C++14 允许在 Lambda表达式的捕获列表中使用初始化表达式,从而实现初始化捕获,即可以在捕获列表中创建和初始化一个新的变量,而不是捕获一个已存在的变量。例如:
#include <iostream>
using namespace std;
int main()
{
// 定义一个 Lambda表达式,使用初始化捕获,创建一个新的变量 z
auto f = [z = 10] (int x, int y) -> int { return x + y + z; };
// 调用 Lambda表达式
cout << f(3, 4) << endl; // 输出 17
return 0;
}
- 捕获 this 指针:C++17 允许在 Lambda表达式的捕获列表中使用
*this,从而实现捕获 this 指针,即可以在 Lambda表达式中访问当前对象的成员变量和成员函数。例如:
#include <iostream>
using namespace std;
// 定义一个类
class Test
{
public:
Test(int n) : num(n) {} // 构造函数,初始化 num
void show() // 成员函数,显示 num
{
cout << num << endl;
}
void add(int x) // 成员函数,增加 num
{
// 定义一个 Lambda表达式,捕获 this 指针
auto f = [*this] () { return num + x; };
// 调用 Lambda表达式
cout << f() << endl;
}
private:
int num; // 成员变量,存储一个整数
};
int main()
{
Test t(10); // 创建一个 Test 对象
t.show(); // 调用成员函数,输出 10
t.add(5); // 调用成员函数,输出 15
return 0;
}
总结
Lambda表达式是 c++11 引入的一个语法糖,它可以用来定义并创建匿名的函数对象,主要用于方便编程,避免全局变量的定义,并且变量安全。Lambda表达式的语法类似于一个函数定义,但它不需要函数名,可以直接定义并使用。Lambda表达式相比于普通函数和普通类,有以下几个优点:简洁、灵活和安全。Lambda表达式本质上是一个匿名类的对象,因此它可以赋值给一个函数指针或函数引用,也可以作为模板参数传递给一个泛型函数或类。C++14 和 C++17 对 Lambda表达式进行了一些扩展和改进,使得 Lambda表达式更加强大和灵活,主要有以下几个方面:泛型 Lambda、初始化捕获和捕获 this 指针。
2.2 自顶向下 DFS
104. 二叉树的最大深度 - 力扣(LeetCode)
思路:普通递归自底向上、自顶向下、层序遍历迭代法
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数或者节点数(取决于深度从0开始还是从1开始)自顶向下
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数或者节点数(取决于高度从0开始还是从1开始)自底向上
而根节点的高度就是二叉树的最大深度,所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。
这一点其实是很多同学没有想清楚的,很多题解同样没有讲清楚。
class Solution {
public:
int maxDepth(TreeNode* root) {
if(!root) return 0;
int l_d = maxDepth(root->left);
int r_d = maxDepth(root->right);
return max(l_d , r_d) + 1;//其实是递归法的后序遍历
}
};
- 时间复杂度:O(n),其中 n 为二叉树的节点个数。
- 空间复杂度:O(n)。最坏情况下,二叉树退化成一条链,递归需要 O(n) 的栈空间。
class Solution {
public:
int maxDepth(TreeNode* root) {
int ans = 0;
auto dfs = [&](auto& dfs , TreeNode* node , int depth)-> void{
if(!node) return;
depth ++;
ans = max(ans , depth);
dfs(dfs , node->left , depth);
dfs(dfs , node->right , depth);
};
dfs(dfs , root , 0);
return ans;
}
};
复杂度同上
层序遍历:
class Solution {
public:
int maxDepth(TreeNode* root) {
queue<TreeNode*> que;
if(root) que.push(root);
int maxDepth = 0;
while(!que.empty()){
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
maxDepth ++;
}
return maxDepth;
}
};
111. 二叉树的最小深度 - 力扣(LeetCode)
思路:
方法一:自顶向下「递」
我们可以在 DFS 这棵树的同时,额外传入一个计数器 cnt,表示路径上的节点个数,例如上图从根到叶子的路径 3→20→15:
递归前,cnt=0。
从 3 开始递归,cnt 加一,现在 cnt=1。
向下递归到 20,cnt 加一,现在 cnt=2。
向下递归到 15,cnt 加一,现在 cnt=3。由于 15 是叶子,用 3 更新答案的最小值。
class Solution {
int ans = INT_MAX;
void dfs(TreeNode* node , int cnt){
if(!node) return;
cnt ++;
if(!node->left && !node->right){//如果是叶子节点更新答案
ans = min(ans , cnt);
return;
}
dfs(node->left , cnt);
dfs(node->right , cnt);
};
public:
int minDepth(TreeNode* root) {
dfs(root , 0);
return root ? ans : 0;
}
};
优化
如果递归中发现
cnt≥ans,由于继续向下递归也不会让 ans 变小,直接返回。这一技巧叫做「最优性剪枝」。
class Solution {
int ans = INT_MAX;
void dfs(TreeNode* node , int cnt){
if(!node || ++cnt >= ans) return;
if(!node->left && !node->right){
ans = cnt;
return;
}
dfs(node->left , cnt);
dfs(node->right , cnt);
};
public:
int minDepth(TreeNode* root) {
dfs(root , 0);
return root ? ans : 0;
}
};
方法二:自底向上「归」
定义dfs(node)表示以节点 node 为根的子树的最小深度。分类讨论:
如果 node 是空节点,由于没有节点,返回 0。
如果 node 没有右儿子,那么深度就是左子树的深度加一,即
dfs(node)=dfs(node.left)+1。如果 node 没有左儿子,那么深度就是右子树的深度加一,即
dfs(node)=dfs(node.right)+1。如果 node 左右儿子都有,那么分别递归计算左子树的深度,以及右子树的深度,二者取最小值再加一,即
dfs(node) = min(dfs(node.left),dfs(node.right))+1注意:并不需要特判 node 是叶子的情况,因为在没有右儿子的情况下,我们会递归 node.left,如果它是空节点,递归的返回值是 0,加一后得到 1,这正是叶子节点要返回的值。
答案:
dfs(root)。代码实现时,可以直接递归调用
minDepth。
class Solution{
public:
int minDepth(TreeNode* root) {
if(!root) return 0;
if(!root->right) return minDepth(root->left) + 1;
if(!root->left) return minDepth(root->right) + 1;
return min(minDepth(root->left) , minDepth(root->right)) + 1;
}
};
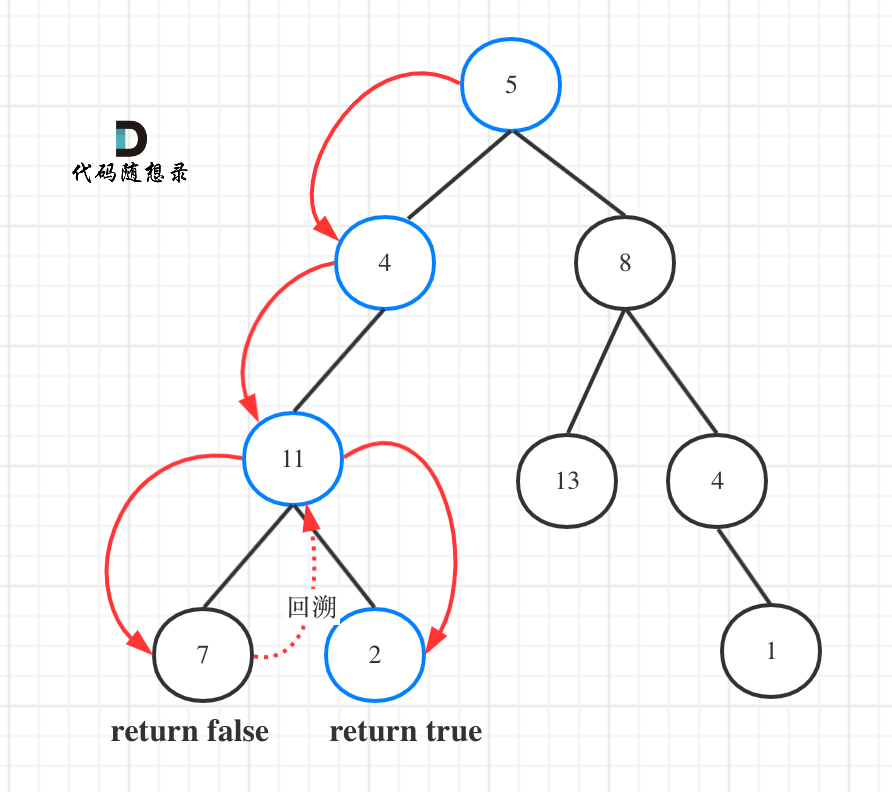
112. 路径总和
思路:递归 || 迭代
先说递归。可以使用深度优先遍历的方式(本题前中后序都可以,无所谓,因为中节点也没有处理逻辑)来遍历二叉树。
- 确定递归函数的参数和返回类型
参数:需要二叉树的根节点,还需要一个计数器,这个计数器用来计算二叉树的一条边之和是否正好是目标和,计数器为int型。
返回值:递归函数什么时候需要返回值?什么时候不需要返回值?这里总结如下三点:
- 如果需要搜索整棵二叉树且不用处理递归返回值,递归函数就不要返回值。(这种情况就是本文下半部分介绍的113.路径总和ii)
- 如果需要搜索整棵二叉树且需要处理递归返回值,递归函数就需要返回值。 (这种情况我们在236. 二叉树的最近公共祖先 (opens new window)中介绍)
- 如果要搜索其中一条符合条件的路径,那么递归一定需要返回值,因为遇到符合条件的路径了就要及时返回。(本题的情况)
而本题我们要找一条符合条件的路径,所以递归函数需要返回值,及时返回,那么返回类型为bool。
class Solution {
bool traversal(TreeNode* cur , int cnt){
if(!cur->left && !cur->right && cnt == 0) return true;
// 遇到叶子节点,并且计数为0
if(!cur->left && !cur->right) return false;
//遇到叶子节点且计数不为0
if(cur->left){
if(traversal(cur->left , cnt - cur->left->val)) return true;
}//蕴含了回溯的过程,cnt的值是不变的
if(cur->right){
if(traversal(cur->right , cnt - cur->right->val)) return true;
}
return false;
}
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if(!root) return false;
return traversal(root , targetSum - root->val);
}
};
精简版:
class Solution {
public:
bool hasPathSum(TreeNode* root, int sum) {
if (!root) return false;
if (!root->left && !root->right && sum == root->val) {
return true;
}
return hasPathSum(root->left, sum - root->val) || hasPathSum(root->right, sum - root->val);
}
};
迭代法:
如果使用栈模拟递归的话,那么如果做回溯呢?
此时栈里一个元素不仅要记录该节点指针,还要记录从头结点到该节点的路径数值总和。用
pair结构来存放这个栈里的元素。定义为:pair<TreeNode*, int>pair<节点指针,路径数值>,这个为栈里的一个元素。如下代码是使用栈模拟的前序遍历,注意顺序是中右左。如下:(详细注释)
class solution {
public:
bool haspathsum(TreeNode* root, int sum) {
if (root == null) return false;
// 此时栈里要放的是pair<节点指针,路径数值>
stack<pair<TreeNode*, int>> st;
st.push(pair<TreeNode*, int>(root, root->val));
while (!st.empty()) {
pair<TreeNode*, int> node = st.top();
st.pop();
// 如果该节点是叶子节点了,同时该节点的路径数值等于sum,那么就返回true
if (!node.first->left && !node.first->right && sum == node.second) return true;
// 右节点,压进去一个节点的时候,将该节点的路径数值也记录下来
if (node.first->right) {
st.push(pair<TreeNode*, int>(node.first->right, node.second + node.first->right->val));
}
// 左节点,压进去一个节点的时候,将该节点的路径数值也记录下来
if (node.first->left) {
st.push(pair<TreeNode*, int>(node.first->left, node.second + node.first->left->val));
}
}
return false;
}
};
129. 求根节点到叶节点数字之和
思路:迭代、递归
迭代法就是上一题的代码,细节是改node每次传递的值为
node.second * 10 + node.first->right>val,碰到叶子节点就收集值。最后累加vec里面的和。递归法首先要搜索所有路径,所以函数类型为空,参数应该有节点、res数组、沿节点搜索的和cnt。
终止条件为节点空 或 叶子节点。
if(!root) return; if(!root->left && !root->right) vec.push_back(cnt);避免访问空指针,每次先判断左右孩子是否空,每次递归下去将cnt改为
cnt * 10 + root->right->val。
class Solution {
public:
int sumNumbers(TreeNode* root) {
if(!root) return 0;
vector<int> res;
stack<pair<TreeNode* , int>> st;
st.push(pair<TreeNode* , int>(root , root->val));
while(!st.empty()){
pair<TreeNode* , int> node = st.top();
st.pop();
if(!node.first->left && !node.first->right ) res.push_back(node.second);
if(node.first->right){
st.push(pair<TreeNode* , int>(node.first->right , 10 * node.second + node.first->right->val));
}
if(node.first->left){
st.push(pair<TreeNode* , int>(node.first->left , 10 * node.second + node.first->left->val));
}
}
int ans = 0;
for (auto i : res) {
ans += i;
}
return ans;
}
};
递归:
class Solution {
void traversal(TreeNode* root ,vector<int>& vec , int cnt){
if(!root) return;
if(!root->left && !root->right) vec.push_back(cnt);
if(root->left) traversal(root->left , vec , 10 * cnt + root->left->val);
if(root->right) traversal(root->right , vec ,10 * cnt + root->right->val);
}
public:
int sumNumbers(TreeNode* root) {
if(!root) return 0;
vector<int> res;
traversal(root , res , root->val);
int ans = 0;
for(auto i : res) ans += i;
return ans;
}
};
灵神的简介写法:
//无返回值
class Solution{
int ans = 0;
void dfs(TreeNode* node , int x){
if(!node) return;
x = x * 10 + node->val;
if(!node->left && !node->right){
ans += x;
return;
}
dfs(node->left , x);
dfs(node->right , x);
}
public:
int sumNumbers(TreeNode* root){
dfs(root , 0);
return ans;
}
};
//有返回值
class Solution{
public:
int sumNumbers(TreeNode* root , int x = 0){
if(!root) return 0;
x = x * 10 + root->val;
if(!root->left && !root->right) return x;
return sumNumbers(root->left , x) + sumNumbers(root->right , x);
}
};




 浙公网安备 33010602011771号
浙公网安备 33010602011771号