11.24&&11.25
11/24
2. 两数相加
思路:创造一个新链表,模拟加法进位过程。
值得注意的就是,当链表一长一短时,链表1先走完,之后处理链表2剩下的部分,测试样例3启发我们还要在最后处理剩下的进位。
看完题解发现写的属于迭代法。
递归法:
把虚线内要计算的内容,可以理解为一个和原问题相似的,规模更小的子问题,所以非常适合用递归解决。
代码实现时,有一个简化代码的小技巧:如果递归中发现 l2 的长度比 l1 更长,那么可以交换 l1 和 l2,保证 l1 不是空节点,从而简化代码逻辑。
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode* cur1 = l1;
ListNode* cur2 = l2;
ListNode* dummy = new ListNode(0);
ListNode* cur = dummy;
int s = 0 , l = 0;
//走公共部分
while(cur1 && cur2){
s = (cur1->val + cur2->val + l) % 10;
l = (cur1->val + cur2->val + l) / 10;
ListNode* cur3 = new ListNode(s);
cur->next = cur3;
cur = cur3;
cur1 = cur1->next;
cur2 = cur2->next;
}
//如果链表1没走完
if(cur1){
while(cur1){
s = (cur1->val + l) % 10;
l = (cur1->val + l) / 10;
ListNode* cur3 = new ListNode(s);
cur->next = cur3;
cur = cur3;
cur1 = cur1->next;
}
}
//如果链表2没走完
else {
while(cur2){
s = (cur2->val + l) % 10;
l = (cur2->val + l) / 10;
ListNode* cur3 = new ListNode(s);
cur->next = cur3;
cur = cur3;
cur2 = cur2->next;
}
}
//还要在最后处理进位
if(l){
ListNode* cur3 = new ListNode(l);
cur->next = cur3;
}
return dummy->next;
}
};
迭代法优雅写法:
**注意:“ . ” 和 “ -> ”的使用 **
用个具体的例子说明:
假设有一个类: ClassA
1、如果声明的是一个对象:ClassA A
则用A.function
2、如果声明的是一个对象指针:ClassA* A=new A;
则用A->function如下面的dummy,如果写成:
ListNode dummy; // 哨兵节点 ListNode* cur = &dummy;最后返回时就要用
return dummy.next;因为dummy不是指针。按照习惯还是定义为指针节点避免错误。
ListNode* dummy = new ListNode(0); ListNode* cur = dummy; return dummy->next;
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode dummy; // 哨兵节点
ListNode* cur = &dummy;
int carry = 0; // 进位
while (l1 || l2 || carry) { // 有一个不是空节点,或者还有进位,就继续迭代
if (l1) {
carry += l1->val; // 节点值和进位加在一起
l1 = l1->next; // 下一个节点
}
if (l2) {
carry += l2->val; // 节点值和进位加在一起
l2 = l2->next; // 下一个节点
}
cur = cur->next = new ListNode(carry % 10); // 每个节点保存一个数位
carry /= 10; // 新的进位
}
return dummy.next; // 哨兵节点的下一个节点就是头节点
}
};
递归法:
class Solution {
public:
// l1 和 l2 为当前遍历的节点,carry 为进位
//直接在原函数里加了一个参数carry传递下去
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2, int carry = 0) {
if (l1 == nullptr && l2 == nullptr) { // 递归边界:l1 和 l2 都是空节点
return carry ? new ListNode(carry) : nullptr; // 如果进位了,就额外创建一个节点
}
if (l1 == nullptr) { // 如果 l1 是空的,那么此时 l2 一定不是空节点
swap(l1, l2); // 交换 l1 与 l2,保证 l1 非空,从而简化代码
}
int sum = carry + l1->val + (l2 ? l2->val : 0); // 节点值和进位加在一起
l1->val = sum % 10; // 每个节点保存一个数位(直接修改原链表)
l1->next = addTwoNumbers(l1->next, (l2 ? l2->next : nullptr), sum / 10); // 进位
return l1;
}
};
445. 两数相加 II
思路:链表翻转+上一题两数相加
class Solution {
private:
ListNode* reverse(ListNode* head){
ListNode* pre = nullptr;
ListNode* cur = head;
while(cur){
ListNode* tmp = cur->next;
cur->next = pre;
pre = cur;
cur = tmp;
}
return pre;
}
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2 ) {
l1 = reverse(l1);
l2 = reverse(l2);
ListNode* dummy = new ListNode(0);
ListNode* cur = dummy;
int carry = 0;
while(l1 || l2 || carry){
if(l1){
carry += l1->val;
l1 = l1->next;
}
if(l2){
carry += l2->val;
l2 = l2->next;
}
cur = cur->next = new ListNode(carry % 10);
carry /= 10;
}
return reverse(dummy->next);
}
};
递归法的写法:
把
翻转函数reverse、两数相加addTwo都写成单独调用的方法。
class Solution {
ListNode* reverseList(ListNode* head) {
if (head == nullptr || head->next == nullptr) {
return head;
}
auto new_head = reverseList(head->next);
head->next->next = head; // 把下一个节点指向自己
head->next = nullptr; // 断开指向下一个节点的连接,保证最终链表的末尾节点的 next 是空节点
return new_head;
}
// l1 和 l2 为当前遍历的节点,carry 为进位
ListNode* addTwo(ListNode* l1, ListNode* l2, int carry = 0) {
if (l1 == nullptr && l2 == nullptr) { // 递归边界:l1 和 l2 都是空节点
return carry ? new ListNode(carry) : nullptr; // 如果进位了,就额外创建一个节点
}
if (l1 == nullptr) { // 如果 l1 是空的,那么此时 l2 一定不是空节点
swap(l1, l2); // 交换 l1 与 l2,保证 l1 非空,从而简化代码
}
carry += l1->val + (l2 ? l2->val : 0); // 节点值和进位加在一起
l1->val = carry % 10; // 每个节点保存一个数位
l1->next = addTwo(l1->next, (l2 ? l2->next : nullptr), carry / 10); // 进位
return l1;
}
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
l1 = reverseList(l1);
l2 = reverseList(l2); // l1 和 l2 反转后,就变成【2. 两数相加】了
auto l3 = addTwo(l1, l2);
return reverseList(l3);
}
};
11/25
2816. 翻倍以链表形式表示的数字
思路:链表翻转+链表相加
注意链表是由高位->低位,因此需要先翻转。
class Solution {
private:
ListNode* reverse(ListNode* head){
ListNode* pre = nullptr;
ListNode* cur = head;
while(cur){
ListNode* tmp = cur->next;
cur->next = pre;
pre = cur;
cur = tmp;
}
return pre;
}
public:
ListNode* doubleIt(ListNode* head) {
head = reverse(head);
ListNode* dummy = new ListNode(0);
int carry = 0;
ListNode* cur = dummy;
while(head || carry){
if(head){
carry += head->val * 2;
head = head->next;
}
cur = cur->next = new ListNode(carry % 10);
carry /= 10;
}
return reverse(dummy->next);
}
};
法二:
由于本题是乘二,进位只可能是0/1的情况。
如果不考虑进位,就是每个节点的值乘以 2。
什么时候会受到进位的影响呢?只有下一个节点大于 4 的时候,才会因为进位多加一。
特别地,如果链表头的值大于 4,那么需要在前面插入一个新的节点。
class Solution {
public:
ListNode* doubleIt(ListNode* head) {
if (head->val > 4) {
head = new ListNode(0, head);
}
for (auto cur = head; cur; cur = cur->next) {
cur->val = cur->val * 2 % 10;
if (cur->next && cur->next->val > 4) {
cur->val++;
}
}
return head;
}
};
21. 合并两个有序链表
思路:新创建一个链表,每次比较较小值放进去,最后剩下的链表剩余部分拼接到后边。
class Solution {
public:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
ListNode* dummy = new ListNode(0);
ListNode* cur = dummy;
ListNode* cur1 = list1;
ListNode* cur2 = list2;
while(cur1 && cur2){
if(cur1->val <= cur2->val) {cur = cur->next = new ListNode(cur1->val);
cur1 = cur1->next;
}
else {
cur = cur->next = new ListNode(cur2->val);
cur2 = cur2->next;
}
}
if(cur1) cur->next = cur1;
else cur->next = cur2;
return dummy->next;
}
};
另外的写法:
class Solution {
public:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
ListNode* dummy = new ListNode(0);
ListNode* cur = dummy;
while(list1 && list2){
if(list1->val <= list2->val) {
cur->next = list1;
list1 = list1->next;
}
else {
cur->next = list2;
list2 = list2->next;
}
cur = cur->next;
}
cur->next = list1 ? list1 : list2;
return dummy->next;
}
};
链表-分治 未完待续···
§2.1 遍历二叉树
二叉树主要有两种遍历方式:
- 深度优先遍历:先往深走,遇到叶子节点再往回走。
- 广度优先遍历:一层一层的去遍历。
这两种遍历是图论中最基本的两种遍历方式,后面在介绍图论的时候 还会介绍到。
那么从深度优先遍历和广度优先遍历进一步拓展,才有如下遍历方式:
- 深度优先遍历
- 前序遍历(递归法,迭代法)
- 中序遍历(递归法,迭代法)
- 后序遍历(递归法,迭代法)
- 广度优先遍历
- 层次遍历(迭代法)
这里前中后,其实指的就是中间节点的遍历顺序.
链式存储的二叉树节点的定义方式。
C++代码如下:
struct TreeNode { int val; TreeNode *left; TreeNode *right; TreeNode(int x) : val(x), left(NULL), right(NULL) {} };递归算法的三个要素。
确定递归函数的参数和返回值: 确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
void traversal(TreeNode* cur, vector<int>& vec)确定终止条件: 写完了递归算法, 运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出。
if (cur == NULL) return;确定单层递归的逻辑: 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
vec.push_back(cur->val); // 中 traversal(cur->left, vec); // 左 traversal(cur->right, vec); // 右binary-tree-preorder-traversal、binary-tree-inorder-traversal、binary-tree-postorder-traversal代码依次如下:
递归法
class Solution {
void traversal(TreeNode* cur , vector<int>& vec){
if(!cur) return;
//traversal函数里这三行换位就实现不同的递归顺序
vec.push_back(cur->val);//中间节点先遍历,谓之前序
traversal(cur->left , vec);
traversal(cur->right , vec);
}
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
traversal(root , res);
return res;
}
};
迭代法
以栈作为数据结构,注意是
st.push(),vector才是push_back()。前序遍历是中左右,每次先处理的是中间节点,那么先将根节点放入栈中,然后将右孩子加入栈,再加入左孩子。
要先加入 右孩子,再加入左孩子,这样出栈的时候才是中左右的顺序。
动画如下:
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> res;
if(!root) return res;
st.push(root);
while(!st.empty()){
TreeNode* node = st.top();//中
st.pop();
res.push_back(node->val);
if(node->right) st.push(node->right);//右
if(node->left) st.push(node->left);//左
//这样出栈顺序就是中左右
}
return res;
}
};
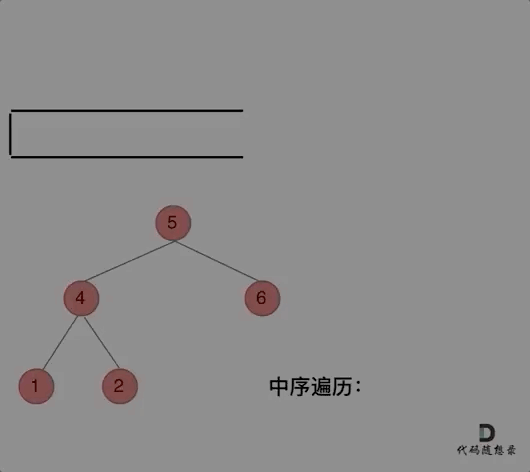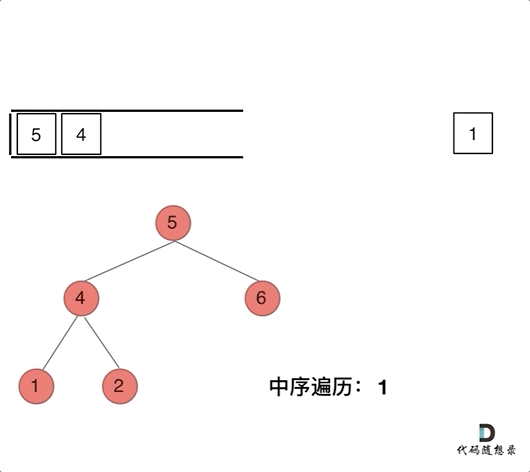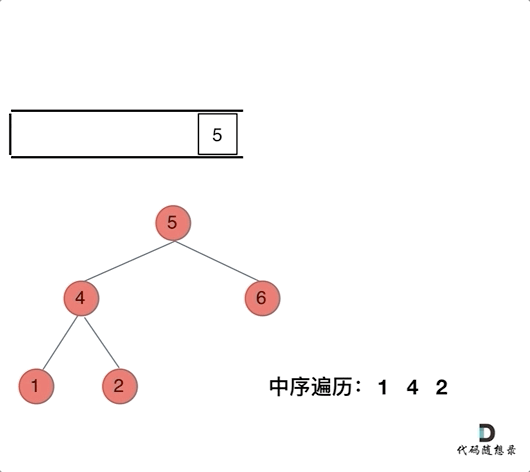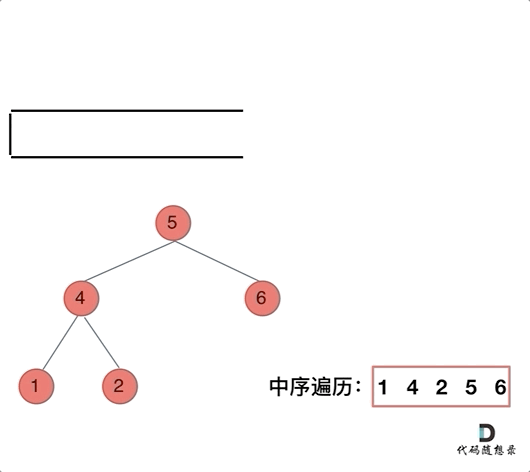
但接下来,再用迭代法写中序遍历的时候,目前的前序遍历的逻辑无法直接应用到中序遍历上。
因为前序遍历的顺序是中左右,先访问的元素是中间节点,要处理的元素也是中间节点,所以刚刚才能写出相对简洁的代码,因为要访问的元素和要处理的元素顺序是一致的,都是中间节点。
那么再看看中序遍历,中序遍历是左中右,先访问的是二叉树顶部的节点,然后一层一层向下访问,直到到达树左面的最底部,再开始处理节点(也就是在把节点的数值放进result数组中),这就造成了处理顺序和访问顺序是不一致的。
那么在使用迭代法写中序遍历,就需要借用指针的遍历来帮助访问节点,栈则用来处理节点上的元素。
动画如下:
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> st;
TreeNode* cur = root;
while(cur || !st.empty()){
//因为一直要把cur入栈,所以不用一开始对cur判空,然后放入
if(cur) { //指针访问节点,一直向左直到最底层
st.push(cur); //将访问节点入栈
cur = cur->left; //左
}
else{
cur = st.top(); // 从栈里弹出的此时是左节点,处理节点
st.pop();
res.push_back(cur->val);//中
cur = cur->right;//右
}
}
return res;
}
};
比较前序:中左右 后序:左右中可以发现,如果将前序变为中右左,再将res数组倒序即可变成左右中后序,因此在前序的代码上改变入栈顺序即可。
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> st;
if(!root) return res;
st.push(root);
while(!st.empty()){
TreeNode* node = st.top();
st.pop();
res.push_back(node->val);
if(node->left) st.push(node->left);//左
if(node->right) st.push(node->right); //右
//这样出栈顺序就是中右左
}
reverse(res.begin() , res.end());
return res;
}
};
二叉树的统一迭代法
以中序遍历为例,使用栈的话,无法同时解决访问节点(遍历节点)和处理节点(将元素放进结果集)不一致的情况。那我们就将访问的节点放入栈中,把要处理的节点也放入栈中但是要做标记。
如何标记呢,就是要处理的节点放入栈之后,紧接着放入一个空指针作为标记。 这种方法也可以叫做标记法。
中序:
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
if (node->right) st.push(node->right); // 添加右节点(空节点不入栈)
st.push(node); // 添加中节点
st.push(NULL); // 中节点访问过,但是还没有处理,加入空节点做为标记。
if (node->left) st.push(node->left); // 添加左节点(空节点不入栈)
} else { // 只有遇到空节点的时候,才将下一个节点放进结果集
st.pop(); // 将空节点弹出
node = st.top(); // 重新取出栈中元素
st.pop();
res.push_back(node->val); // 加入到结果集
}
}
return res;
}
};
看代码有点抽象我们来看一下动画(中序遍历):可以看出我们将访问的节点直接加入到栈中,但如果是处理的节点则后面放入一个空节点, 这样只有空节点弹出的时候,才将下一个节点放进结果集。

前序:仅改相应部分代码为中左右的倒序即可。
if (node != NULL) {
st.pop();
if (node->right) st.push(node->right); // 右
if (node->left) st.push(node->left); // 左
st.push(node); // 中
st.push(NULL);
}
后序:仅改相应部分代码为左右中的倒序即可。
if (node != NULL) {
st.pop();
st.push(node); // 中
st.push(NULL);
if (node->right) st.push(node->right); // 右
if (node->left) st.push(node->left); // 左
872. 叶子相似的树
思路:
如果左右孩子均为空则加入容器。
class Solution {
void traversal(TreeNode* cur , vector<int>& vec){
if(!cur) return;
if(!cur->left && !cur->right) vec.push_back(cur->val);
traversal(cur->left , vec);
traversal(cur->right , vec);
}
public:
bool leafSimilar(TreeNode* root1, TreeNode* root2) {
vector<int> res1 , res2;
traversal(root1 , res1);
traversal(root2 , res2);
return res1 == res2;
}
};
LCP 44. 开幕式焰火
思路:集合遍历保存节点不同值的个数
class Solution {
void traversal(TreeNode* root , unordered_set<int>& mp){
if(!root) return;
mp.insert(root->val);
traversal(root->left , mp);
traversal(root->right , mp);
}
public:
int numColor(TreeNode* root) {
unordered_set<int> mp;
traversal(root , mp);
return mp.size();
}
};
复习一下
unordered_set的用法:在C++标准库中,unordered_set是一个使用
哈希表实现的集合(set)容器,用于存储唯一的元素,且元素的存储没有特定的顺序。unordered_set使用哈希函数来将元素映射到桶中,不同的元素可能映射到同一个桶中,但是这些元素的哈希值不同。
insert()函数:用于插入元素,语法为:std::unordered_set<int> myset; myset.insert(3); myset.insert(1); myset.insert(7);
find()函数:用于查找元素,语法为:std::unordered_set<int> myset = {1, 2, 3}; auto it = myset.find(2); if (it != myset.end()) std::cout << "Element found in unordered_set: " << *it << std::endl; else std::cout << "Element not found in unordered_set" << std::endl;
erase()函数:用于删除元素,语法为:std::unordered_set<int> myset = {1, 2, 3}; myset.erase(2);
size()函数:返回unordered_set中元素的数量,语法为:std::unordered_set<int> myset = {1, 2, 3}; std::cout << "unordered_set size: " << myset.size() << std::endl;
empty()函数:检查unordered_set是否为空,语法为:std::unordered_set<int> myset; if (myset.empty()) std::cout << "unordered_set is empty" << std::endl; else std::cout << "unordered_set is not empty" << std::endl;
clear()函数:用于清空unordered_set中的所有元素,语法为:std::unordered_set<int> myset = {1, 2, 3}; myset.clear();这些函数是unordered_set中最常用的一些函数。除此之外,还有一些其他的函数,如
bucket(),load_factor()和max_load_factor()等,它们用于查询哈希表的桶的数量、负载因子和最大负载因子等信息。
404. 左叶子之和
思路:迭代/递归
要通过节点的父节点来判断其左孩子是不是左叶子了。
左叶子的明确定义:节点的左孩子不为空,且左孩子的左右孩子都为空(说明是叶子节点),那么节点的左孩子为左叶子节点,代码逻辑如下:
if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) { 左叶子节点处理逻辑 }
递归:递归的遍历顺序为后序遍历(左右中),是因为要通过递归函数的返回值来累加求取左叶子数值之和。
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if (root == NULL) return 0;
if (root->left == NULL && root->right== NULL) return 0;
int leftValue = sumOfLeftLeaves(root->left); // 左
if (root->left && !root->left->left && !root->left->right) { // 左子树就是一个左叶子的情况
leftValue = root->left->val;
}
int rightValue = sumOfLeftLeaves(root->right); // 右
int sum = leftValue + rightValue; // 中
return sum;
}
};
迭代:简单易懂,无所谓什么遍历方式,关键就是判断左叶子的代码。
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
stack<TreeNode*> st;
if(!root) return 0;
st.push(root);
int res = 0;
while(!st.empty()){
TreeNode* node = st.top();
st.pop();
if(node->left && !node->left->left && !node->left->right) res += node->left->val;
if(node->right) st.push(node->right);
if(node->left) st.push(node->left);
}
return res;
}
};
另解:直接传递参数is_left向左时自动为true,不用再判断父节点。
class Solution {
public:
int result;
void dfs(TreeNode* root, bool is_left) {
if(!root) return;
dfs(root->left, true);
dfs(root->right, false);
if(!root->left && !root->right && is_left) {
result += root->val;
}
}
int sumOfLeftLeaves(TreeNode* root) {
result = 0;
dfs(root, false);
return result;
}
};




 浙公网安备 33010602011771号
浙公网安备 33010602011771号