11.5二分法
11/5
每日一题:3222. 求出硬币游戏的赢家
给你两个 正 整数 x 和 y ,分别表示价值为 75 和 10 的硬币的数目。
Alice 和 Bob 正在玩一个游戏。每一轮中,Alice 先进行操作,Bob 后操作。每次操作中,玩家需要拿出价值 总和 为 115 的硬币。如果一名玩家无法执行此操作,那么这名玩家 输掉 游戏。
两名玩家都采取 最优 策略,请你返回游戏的赢家。
示例 1
输入:x = 2, y = 7
输出:"Alice"
解释:
游戏一次操作后结束:
- Alice 拿走 1 枚价值为 75 的硬币和 4 枚价值为 10 的硬币。
示例 2:
输入:x = 4, y = 11
输出:"Bob"
解释:
游戏 2 次操作后结束:
- Alice 拿走 1 枚价值为 75 的硬币和 4 枚价值为 10 的硬币。
- Bob 拿走 1 枚价值为 75 的硬币和 4 枚价值为 10 的硬币。
提示:
1 <= x, y <= 100
思路:
直接模拟即可
class Solution {
public:
string losingPlayer(int x, int y) {
int turn = 1;
//注意样例(1,4)的边界情况,要加“=”
while(x >= 1 && y >= 4) {
x -= 1;
y -= 4;
turn ++;
}
if(turn % 2 == 0) return "Alice";
else return "Bob";
}
};
704. 二分查找
重点:
TLE了
对区间的定义没有理解清楚,在循环中没有始终坚持根据查找区间的定义来做边界处理。
区间的定义就是不变量,在循环中坚持根据查找区间的定义来做边界处理,就是循环不变量规则。
针对数组无重复元素且有序的前提:
二分法的前提条件:有序数组、数组中无重复元素
二分法定义一般两种,左闭右闭即[left, right],或者左闭右开即[left, right)。
- 左闭右闭时,初始定义
l = 0 , r = nums.size() - 1,判断条件为while(l <= r), 更新区间为l = mid + 1 , r = mid - 1 - 左闭右开时,初始定义
l = 0 , r = nums.size(),判断条件为while(l < r), 更新区间为l = mid + 1 , r = mid
举例:在数组nums:[1,2,3,4,7,9,10]中查找元素targrt = 2,如图所示:(注意区别)

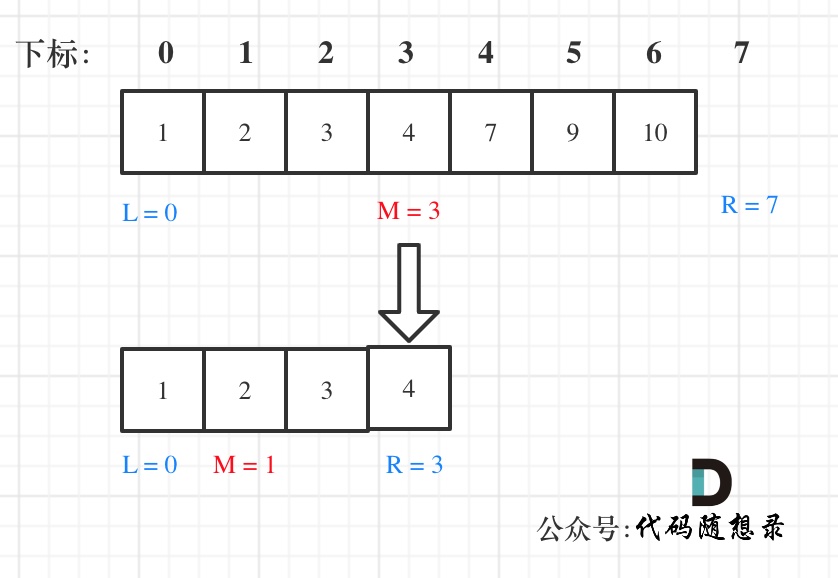
用统一的优雅代码:定义左右边界为-1、n
class Solution {
public:
int search(vector<int>& nums, int target) {
int l = -1;
int r = nums.size();
while(l + 1 != r){
int mid = l + ((r - l) >> 1);
if(target < nums[mid]) r = mid;
else if(target > nums[mid]) l = mid ;
else return mid ;
}
return -1;
}
};
拓展(如果数组元素有重复)
1. 是否可以使用二分法的关键在于:二分后,能否判断出答案所在的区间,而不是数据是否有序。
2.防溢出计算mid(移位+用减法计算中间索引)
int mid = l + ((r - l ) >> 1)//这里两个括号,移位运算的优先级跟加减一样
3. 如何优雅的处理边界条件?
对于一个有序数组,假设下标为0,1,2,3…,n-1;总共n个数字(不要求数字不重复)。指针L要赋值为-1,指针R要赋值为n
无论何种情况,初始的L+1始终小于R,历经循环后最终L和R相邻,不会出现一开始L就和R重合等情况导致出现while(L+1!=R)循环不能结束的情况。
我们就能够通过二分得到不重合的两区间,而且只需要L=mid和R=mid,不需要考虑L=mid+1,R=mid-1的情况
记得是对于一个下标为0,1,2…n-1的数组,模板为:
int L = -1 , R = n;
while( L + 1 != R)
{
int mid = L + R >> 1;
if(check()) L = mid;
else R = mid;
//最后根据你所分左右两边区间的结果
//选取L或者R作为结果
}
如例题找最后出现的位置(或找第一次出现的位置):
给定一个排好序的整数数组a,数组中可能存在重复元素。给定数组中的一个值target,求出它最后出现的位置。
例如数组nums为:[1 3 3 3 5],目标值target = 3。nums中最后一个等于3的元素为:nums[3],所以结果为3。
int findLast(vector<int> nums,int t){
int l = -1, r = nums.size();
while (l + 1 != r){//l<r进行二分,直到l=r时,停止二分
int mid = l + ((r - l ) >> 1);//下方语句,出现了l = mid,mid要用(l + r + 1) / 2计算
if (nums[mid] > t)//nums[mid] > t,t最后一次出现的位置一定在mid之前
r = mid ;
else //nums[mid] <= t,t最后一次出现的位置一定在mdi处或者mid之后
l = mid;//出现了l = mid,mid要用(l + r + 1) / 2计算
}
return l;
}
如果找第一次出现的位置,则相应的代码逻辑为:(r指针取等)
if(nums[mid] < k) l = mid;
else r = mid;
如一道综合例题:
AcWing 789. 数的范围
#include <iostream>
#include <vector>
using namespace std;
const int N = 1e5 + 10;
vector<int> nums(N);
int main(){
int n , q , k ;
cin >> n >> q;
for (int i = 0; i < n; i++) cin >> nums[i];
while(q --){
cin >> k;
//找第一次出现的位置r
int l = -1 , r = n;
while(l + 1 != r){
int mid = l + ((r - l) >> 1);
if(nums[mid] < k) l = mid;
else r = mid; //此时r是第一次出现的位置
}
if(nums[r] != k) cout << "-1 -1" << endl;
else{ //对应于k已经出现在数组中的情况
cout << r << " ";
int ll = -1 , rr = n;
while(ll + 1 != rr){
int mid = ll + ((rr - ll) >> 1);
if(nums[mid] > k) rr = mid;
else ll = mid;//此时ll是最后一次出现的位置,如果就只出现一次,则ll = r
}
cout << ll << endl;
}
}
return 0;
}
35.搜索插入位置
思路:
优雅法,找到了
target返回mid,没找到返回r(代入样例试试,其实是该数字应该第一次出现的位置)
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int l = -1;
int r = nums.size();
while(l + 1 != r){
int mid = l + ((r - l) >> 1);
if(nums[mid] < target) l = mid;
else if(nums[mid] > target) r = mid;
else return mid;
}
return r;
}
};
34. 在排序数组中查找元素的第一个和最后一个位置
思路:
没啥好说的,跟上面acwing那题一样。
值得注意的点
本题函数是
searchRange,格式为vector,因此要定义一个vector<int> res,cout 改为return res;也可不定义,但要
return{-1 , -1}其次,
vector的push_back()只能一个个地加进去,且是小括号(),不是大括号{}if判断里两个条件的由来:对于特殊样例的判断,比如:
- nums = { },target = 0,初始l = -1 , r = 1 , mid = 0,一次while后 r = mid = 0,此时满足
nums[r] != target- nums = {2 , 2} , target = 3,初始l = -1 , r = 2 mid = 0,一次while后l = mid = 0,两次while后 l = (0 + 2)/2 = 1;跳出while时 l = 1 , r = 2 此时满足
r == nums.size(),即r越界了,数组中不存在target 。
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int l = -1;
int r = nums.size();
while(l + 1 != r){
int mid = l + ((r - l) >> 1);
if(nums[mid] < target) l = mid;
else r = mid;
}
if(r == nums.size() || nums[r] != target) {
return {-1 , -1};
}
else {
int ll = -1;
int rr = nums.size();
while(ll + 1 != rr){
int mid = ll + ((rr - ll) >> 1);
if(nums[mid] > target) rr = mid;
else ll = mid;
}
return {r , ll};
}
}
};
69. x 的平方根
本题一开始没有AC,问题在于
mid*mid的溢出问题,强制类型转换(long long)要加括号。将本题抽象,相当于找第一次出现\(\sqrt{x}\)的地方r,如果它是整数,那么
(long long)r*r== x,返回r;否则说明是小数,返回整数部分l。
二分法:
class Solution {
public:
int mySqrt(int x) {
int l = -1;
int r = x;
while(l + 1 != r){
int mid = (l + r) / 2;
if((long long)mid * mid < x) l = mid;
else r = mid;
}
if((long long)r * r == x) return r;
else return l;
}
};
官网的另解:
公式法 : \(e^{\frac{1}{2} \ln{x}} = \sqrt{x}\),于是计算
exp(0.5 * log(x)),算完要找出ans与ans + 1哪个是答案。
class Solution {
public:
int mySqrt(int x) {
if (x == 0) {
return 0;
}
int ans = exp(0.5 * log(x));
return ((long long)(ans + 1) * (ans + 1) <= x ? ans + 1 : ans);
}
};
367. 有效的完全平方数
思路:用优雅法
将本题抽象,相当于找第一次出现
target的地方,为r的值,再验证r*r== num即可
class Solution {
public:
bool isPerfectSquare(int num) {
int l = -1;
int r = num;
while(l + 1 != r){
int mid = (l+r) / 2;
if((long long)mid * mid < num) l = mid;
else r = mid;
}
if((long long)r * r == num) return true;
return false;
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号