T2,3,4,5,9动态背包问题
前言
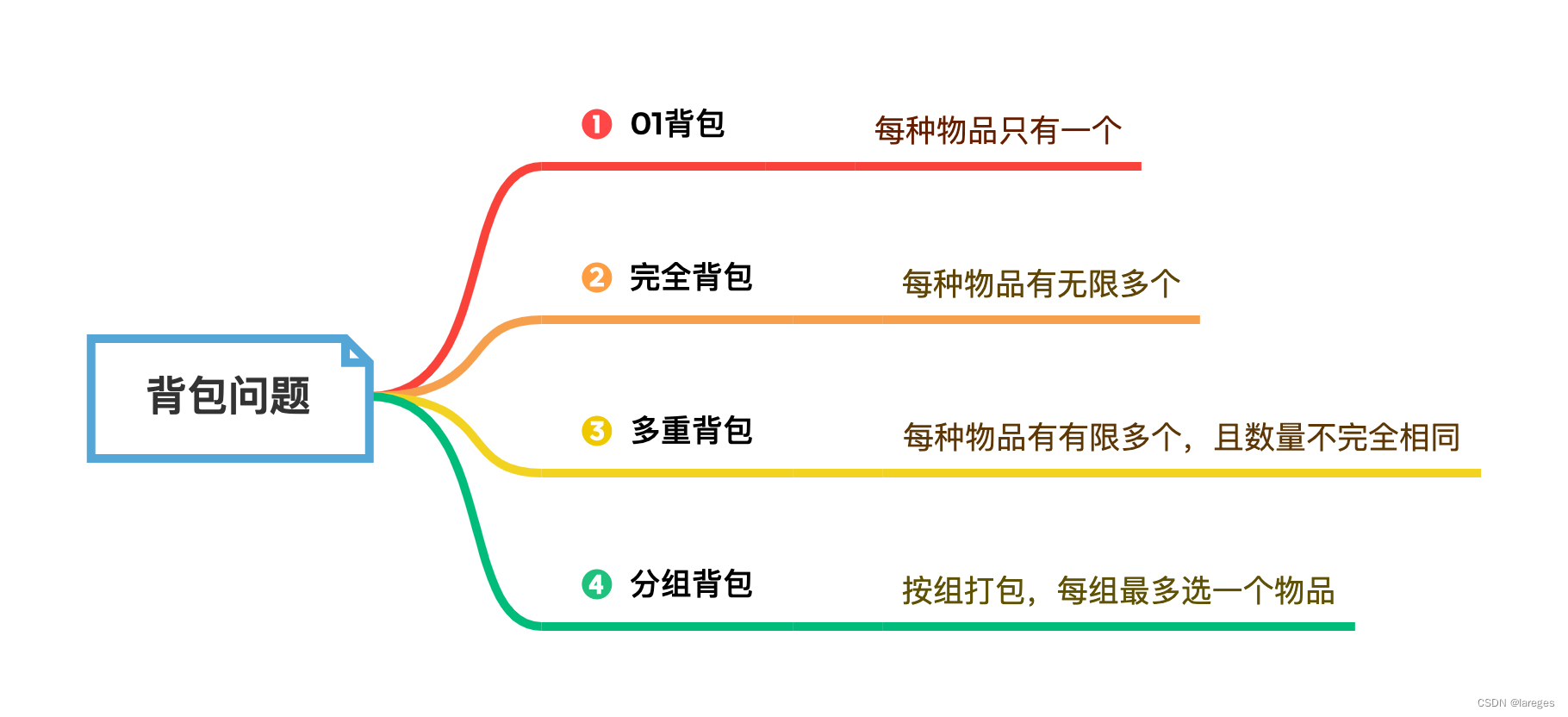
本文主要介绍常见的四种背包问题,思维导图如下:
一、01背包
💡 现有 N 件物品和一个最多能承重 M 的背包,第 i 件物品的重量是 wi,价值是 vi。在背包能承受的范围内,试问将哪些物品装入背包后可使总价值最大,求这个最大价值。
因为每件物品只有选与不选两种状态,所以该问题又称01背包问题。

题目链接:AcWing 2. 01背包问题
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int w[N], v[N];
int dp[N][N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> w[i] >> v[i];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (j < w[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
}
}
cout << dp[n][m] << "n";
return 0;
}
时间复杂度为O(nm)。
1.1 使用滚动数组优化

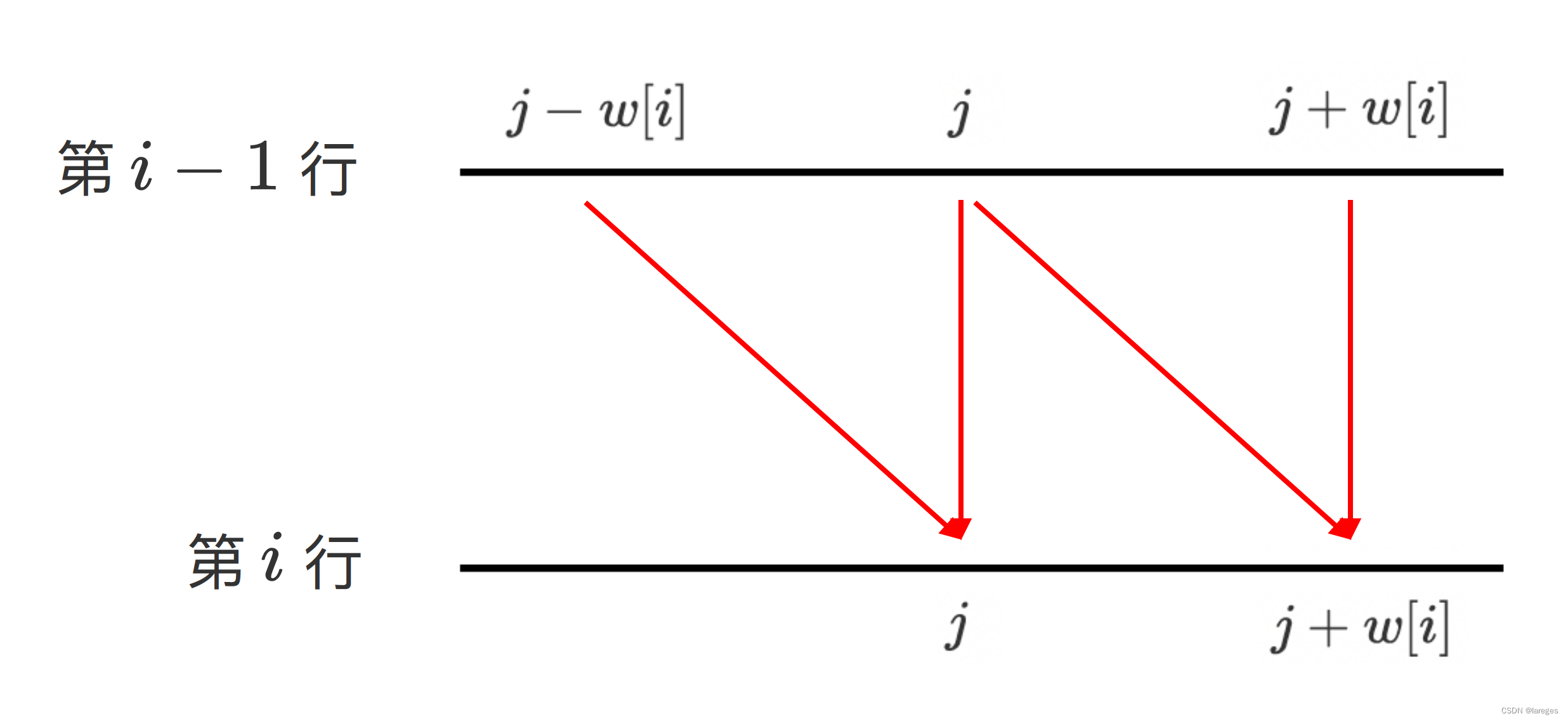

⚠️ 请牢记该式,后续讲解完全背包时会提到它。
这显然是错误的。事实上,让 j 从大到小遍历就不会出现这个问题。
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int w[N], v[N];
int dp[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> w[i] >> v[i];
for (int i = 1; i <= n; i++)
for (int j = m; j >= w[i]; j--)
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
cout << dp[m] << "n";
return 0;
}
当然,w 数组和 v 数组也是不必要的,我们可以边输入边处理,因此可以得到01背包问题的最终版代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int dp[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;//n是物体数量,m是背包容积
for (int i = 1; i <= n; i++) {
int w, v;
cin >> w >> v;//w: weight v: value
for (int j = m; j >= w; j--)
dp[j] = max(dp[j], dp[j - w] + v);
}
cout << dp[m] ;
return 0;
}
到此为止,可以总结出,当dp 数组是二维数组时, j 既可以从小到大遍历也可以从大到小遍历,但当 dp 数组是一维数组时, j只能从大到小遍历。
二、完全背包
💡 现有 N 种物品和一个最多能承重 M 的背包,每种物品都有无限个,第 i 种物品的重量是 wi,价值是 vi。在背包能承受的范围内,试问将哪些物品装入背包后可使总价值最大,求这个最大价值。

题目链接:AcWing 3. 完全背包问题
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int w[N], v[N];
int dp[N][N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> w[i] >> v[i];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
int t = j / w[i];
for (int k = 0; k <= t; k++)
dp[i][j] = max(dp[i][j], dp[i - 1][j - k * w[i]] + k * v[i]);
}
cout << dp[n][m] << "n";
return 0;
}

2.1 使用滚动数组优化


根据1.1节中的结论,该式对应的是 j 从小到大遍历,于是我们只需把01背包问题的代码中的 j 改为从小到大遍历即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int dp[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
int w, v;
cin >> w >> v;
for (int j = w; j <= m; j++) // 只需修改这一行
dp[j] = max(dp[j], dp[j - w] + v);
}
cout << dp[m] << "n";
return 0;
}
优化后的时间复杂度为 O ( n m ) O(nm) O(nm)。
三、多重背包
💡 现有 N 种物品和一个最多能承重 M 的背包,第 i 种物品的数量是 si,重量是 wi,价值是 vi。在背包能承受的范围内,试问将哪些物品装入背包后可使总价值最大,求这个最大价值。

题目链接:AcWing 4. 多重背包问题
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int dp[N][N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
int w, v, s;
cin >> w >> v >> s;
for (int j = 1; j <= m; j++) {
int t = min(s, j / w); // 只有这里需要修改
for (int k = 0; k <= t; k++)
dp[i][j] = max(dp[i][j], dp[i - 1][j - k * w] + k * v);
}
}
cout << dp[n][m] << "n";
return 0;
}

3.1 使用二进制优化

题目链接:AcWing 5. 多重背包问题 II

#include <bits/stdc++.h>
using namespace std;
const int N = 11010, M = 2010;
int w[N], v[N];
int dp[M];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
int cnt = 0;
while (n--) {
int a, b, s; // a是重量, b是价值, s是数量
cin >> a >> b >> s;
for (int k = 1; k <= s; k *= 2) {
cnt++;
w[cnt] = a * k, v[cnt] = b * k;
s -= k;
}
if (s > 0) {
cnt++;
w[cnt] = a * s, v[cnt] = b * s;
}
}
n = cnt;
for (int i = 1; i <= n; i++)
for (int j = m; j >= w[i]; j--)
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
cout << dp[m] << "n";
return 0;
}
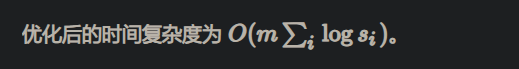
四、分组背包
💡 现有 N 组物品和一个最多能承重 M 的背包,每组物品有若干个,同一组内的物品最多只能选一个。每件物品的重量是 wij,价值是vij,其中 i 是组号,j 是组内编号。在背包能承受的范围内,试问将哪些物品装入背包后可使总价值最大,求这个最大价值。

题目链接:AcWing 9. 分组背包问题
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int w[N][N], v[N][N], s[N];
int dp[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> s[i];
for (int j = 1; j <= s[i]; j++)
cin >> w[i][j] >> v[i][j];
}
for (int i = 1; i <= n; i++)
for (int j = m; j >= 1; j--)
for (int k = 1; k <= s[i]; k++)
if (j >= w[i][k])
dp[j] = max(dp[j], dp[j - w[i][k]] + v[i][k]);
cout << dp[m] << "n";
return 0;
}
总结
我们可以用一个公式来表示01背包、完全背包和多重背包:
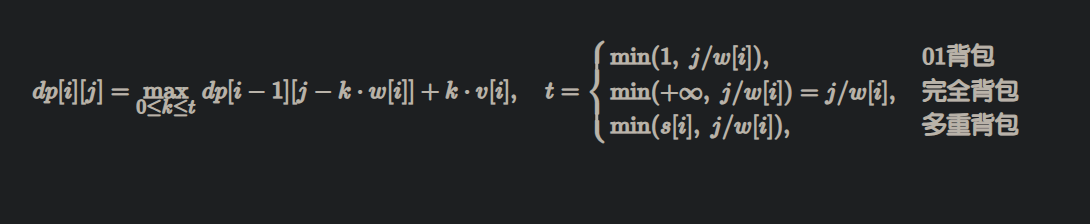

 本文主要介绍常见的四种背包问题
本文主要介绍常见的四种背包问题

 浙公网安备 33010602011771号
浙公网安备 33010602011771号