SURF算法的一篇翻译与论证
原文地址:http://www.sohu.com/a/157742015_715754
SURF: Speeded Up Robust Features
摘要
本文提出了一种新型的具有尺度和旋转不变特性的兴趣点检测和描述方法,简称为SURF(Speeded Up Robust Features)。在可重复性、独特性和鲁棒性方面,与前人提出的方法相比,该方法性能接近甚至更好,但其计算和匹配的速度更快。
该方法得以实现,是依赖于用积分图像来计算图像卷积,建立在现有的先进检测和描述算子(基于Hessian矩阵的检测算子,基于分布特性的描述算子)的基础上,并将这些方法进行简化,只保留必要的部分。该方法是将新型的检测、描述和匹配步骤组合在一起而得到。本文给出了该方法应用于一个标准测试集的实验结果,以及针对现实生活中物体识别应用的实验结果。两种情形下,SURF都表现良好。
1 简介
寻找两幅图像相同场景或物体的兴趣点,是很多计算机视觉应用领域的一个组成部分,例如照相机标定、三维重建、图像配准以及物体识别等。本文的任务就是搜索不同图像中的兴趣 ,可以分成三个主要的步骤。第一,选择图像中特殊的位置点作为兴趣点,如角点、斑点、T形连接点(T-junction)。兴趣点检测最重要的性质是可重复性,即在不同的观察条件下,能否可靠地找到相同的兴趣点。第二,每个兴趣点的邻域用一个特征向量表示。这个描述算子必须是独特的,同时对噪声、错误的检测点、几何和亮度变化是鲁棒的。最后,描述向量在不同的图像之间进行匹配。匹配通常是基于向量之间的距离,如Mahalanobis或Euclidean距离。描述向量的维度对匹配的计算时间有重要影响,所以希望减小描述向量的维度。
我们的目标是开发出一种检测和描述算子,与现有的方法相比,计算更快但又不牺牲性能。为了实现目标,必须要妥善的处理上述要求,比如减小描述向量的维度和复杂度,同时又要保持足够的独特性。
参考文献[1-6]提出了大量的检测和描述方法。文献[7-9]给出了这些算法作用于标准数据集的详细的比较和评估。我们开发快速的检测和描述算子时,从前人的工作中得到一些概念,总结出了对算法性能有影响的一些因素。在我们基于标准数据集以及现实生活中物体识别的实验中,检测和描述算法不仅速度更快,且独特性更好,可重复性也没有减少。
在处理局部特征时,首先需要明确的问题是对不变性水平的要求。很明显,这取决于几何和光照变化程度,而它们又取决于拍照条件的变化。我们关注具有尺度和旋转不变性的检测算子和描述算子。这样可以在特征的复杂度和对常见变形的鲁棒性之间,找到了一个很好的妥协办法。偏斜(skew)、不等比变形和透视效应被认为是二阶的效应为了进一步提高描述子的鲁棒性可能需要处理这些二阶效应。 Lowe[2]也提到,处理完全的仿射不变性增加的复杂性通常会对鲁棒性产生负面影响,并且这么做是不值得的,除非真的要处理非常大的视角变化。在某些情况下,甚至可以不考虑旋转不变性,检测算子退化成只考虑尺度不变的版本,我们把它叫做‘upright SURF’(U-SURF)。确实,在很多应用场景下,例如移动机器人导航或者游客视觉引导,照相机仅仅绕垂直轴旋转。在这种情形下,完全不考虑旋转不变性不仅能加快计算速度,同时能增加识别能力。对于图像的亮度变化,我们定义了一种关于变化因数和偏移量的线性模型。需要注意的是我们的检测和描述算子都没有使用颜色信息。
本文的结构如下,第2部分介绍相关的工作,这些构成我们算法的基础;第3部分介绍兴趣点检测算法;第4部分介绍新型的描述算子;第5部分展示实验结果;第6部分是对全文的总结。
2 相关工作
兴趣点检测使用最广泛的检测算法应该是Harris角点检测[10],最早在1988年提出,它是基于二阶矩构成的矩阵的特征值。然而Harris角点检测不是尺度不变的。Lindeberg提出了一种自动选择尺度的概念[1]。这样就可以使用每一幅图像自有的特征尺度来检测兴趣点。他用Hessian矩阵的行列式值和Laplacian做实验检测斑点状结构,其中Laplacian是Hessian矩阵的迹(即主对角线之和)。Mikolajczyk和Schmid对这个方法进行了改进,他们把Harris-Laplace和Hessian-Laplace结合在一起[11], 创造出了一种鲁棒的、尺度不变、重复检测率很高的检测算子。他们使用尺度自适应的Harris度量标准,或者Hessian矩阵的行列式值来选择位置,使用Laplacian来选择尺度。为了提高计算速度,Lowe[12]使用高斯差分(DoG)来近似高斯Laplace(LoG)。
学者们还提出了很多其他的尺度不变的兴趣点检测算子。Kadir和Brady[13]提出的重点区域检测(salient region detector)是其中的一个例子,该方法最大化区域内的熵。Jurie等[14]提出了基于边缘的区域检测算子。但是这些方法似乎都不太容易加快计算速度。也有学者提出了仿射不变的特征检测算子,能够应对更大的视角变化。但是,这超出了本文研究的范围。
通过研究现有的检测算子,以及关于它们之间比较的文献[15,8],我们得出了以下结论:
(1)基于Hessian矩阵的检测算子比基于Harris的检测算子要稳定,且重复检测率更高。使用Hessian矩阵的行列式值比使用它的迹(Lapacian)更有优势,因为在细长的、局部不均匀的结构检测时失败的机率较低。
(2)类似DoG的近似会提高计算速度,且精度不会牺牲太多。
特征描述人们提出了更多种类的特征描述算子,例如高斯微分[16],不变矩[17],复数特征(complex features)[18,19],可控滤波器(steerable filters)[20],基于相位的局部特征[21],和表示兴趣点的邻域内较小尺度的特征的分布的特征算子。Lowe[2]提出的方法,也就是前面提到的最后一种,比其他的方法性能更好[7]。可以这么来解释,该方法描述了大量图像强度在空间分布的信息,同时也会对小变形和定位误差比较鲁棒。这种检测算子[2],简称为SIFT,计算兴趣点邻域内梯度幅值的直方图,保存在一个128维的向量中(8个方向对每个4×4的位置分区内)。
基于SIFT提出了很多改进的算法。Ke和Sukthankar[4]将PCA应用于梯度图像。这种PCA-SIFT方法,得到一个36维的描述向量,匹配速度更快。但是在Mikolajczyk等[8]的第二个比较研究中,证实它比SIFT的独特性要差,且计算特征向量的时间较长,减弱了快速匹配带来的改进效果。在同一篇文章中[8],作者提出了SIFT的一个变种,叫做GLOH,使用相同维度的描述算子,独特性比SIFT更好。然而,GLOH计算代价更高。
在实际应用中,SIFT描述算子似乎仍然是最吸引人的描述算子,所以目前使用也最广泛。它的独特性较好,并且相对来说计算速度较快,这对在线应用场景极其重要。最近,Se等[22]在FPGA上实现了SIFT,将其速度提高了一个数量级。然而在匹配阶段,SIFT描述向量较大的维度是它的一个缺点。对于普通PC机上的在线应用,检测、描述、匹配,这三个步骤的计算速度仍然都需要加快。Lowe提出了一种最优节点优先算法(best-bin-first)[2],提高了匹配计算的速度,但会导致精度有所降低。
本文的方法 本文提出了一种新型的检测-描述算法,简称为SURF(Speed-Up Robust Features)。检测算子是基于Hessian矩阵[11,1],但是使用了非常基础的近似,就像DoG[2]是一个非常基础的基于Laplacian的检测算子。SURF依赖于积分图像以减少计算时间,因此我们叫它‘Fast-Hessian’检测算子。另一方面,描述算子描述了兴趣点邻域内Haar小波响应的分布特性。我们再一次利用积分图像计算小波响应,以加快计算速度。同时,仅使用64维向量,较少特征向量及其匹配的计算时间,但同时又提高了鲁棒性。我们也提出了一种基于Laplacian符号的新的索引方法,这样不仅提高了匹配的速度,也提高了描述算子的鲁棒性。
为了提高本文的独立可阅读性,下面简洁地介绍积分图像的概念,它是在文献[23]被定义的。积分图像能够快速实现盒状滤波器的卷积运算(box type convolution)。积分图像在点
![]()
的值是输入图像I在点x和原点组成的矩形区域内所有像素点的和,。计算出之后,仅需要额外的四步就可计算出任何垂直的矩形区域内的像素强度之和,与该矩形区域的尺寸大小无关。
3. 快速海森检测(Fast-Hessian Detector)
本文的检测算法基于Hessian矩阵,因为它的计算速度和精度都较好。然而,我们没有针对位置和尺度的选择使用不同的标准(Hessian-Laplace检测算子是这么做的[11]),而是选择Hessian矩阵的特征值同时作为位置和尺度选择的标准。
给定图像I上的一个像素点,给定尺度后x点的Hessian矩阵按下式定义
![]()
式中是Gaussian二阶偏微分
![]()
与图像I的卷积在x点的值,其他两项和与此类似。
对于尺度空间的分析,高斯卷积是最佳的,文献[24]给出解释。然而在实践中,Gaussian需要进行离散和裁剪(图1左半部分),即使使用Gaussian滤波器,只要对得到的图像进行降采样混叠仍会发生。降低分辨率时不会有新的结构出现,这一性质的一维情况已经得到证明,但是人们普遍知道推广到二维时并不成立[25]。在这点上来说,高斯核好像被某种程度的高估了,因此我们测试了一个更简单的可选方案。由于高斯滤波器不是在所有情况下都是理想的,并且考虑到Lowe's近似计算LoG所取得的成功,我们使用盒子滤波器(图1的右半部分)对LoG 做更进一步的近似。这些盒子滤波器近似代替Gausian核的二阶微分,利用积分图像可以快速计算得到卷积结果,并且速度与滤波器的尺寸无关。从结果展示部分5可看出,其性能与使用经过离散和裁剪的高斯核是相当的。
图1给出的9×9盒子滤波器是=1.2的高斯核的二阶微分的近似,以此作为我们最小的尺度(即最高的空间分辨率)。用,和表示近似值。矩形区域内各点的权重比较简单以保证高的计算效率,但是需要进一步修正Hessian矩阵行列式计算表达式各项的权重,
![]()
,其中是Frobenius范数。因此行列式的最终计算式为
然后滤波之后的结果用滤波器的尺寸进行归一化,这样就保证了对不同的滤波器尺寸,Frobenius范数的结果相同。

图1 从左至右:经过离散和裁剪的Gaussian二阶偏微分在y向和xy方向,我们使用盒子滤波器对它们的近似,灰色的区域值为0。
尺度空间通常表示成图像金字塔。图像被一个高斯滤波器反复平滑,并且为了得到金字塔的更高层被连续降采样。由于使用了盒子滤波器和积分图像,不需要使用相同的滤波器依次作用于上次得到的图像,而是使用任意尺寸的这种滤波器以完全相同的速度作用于原始图像,甚至可以做到并行计算(虽然本文还没有使用并行计算)。因此,尺度空间通过增大滤波器的尺寸进行分析,而不是依次缩小图像的尺寸。上文的9×9滤波器的结果作为尺度空间的第一层,我们将其记做尺度(与的高斯微分相对应)。尺度空间接下来的层,通过逐渐增大滤波器的尺寸得到,考虑到积分图像的离散特性和滤波器特殊的结构。滤波器的尺寸可以为9×9,15×15,21×21,27×27等。尺度较大时,相邻两个滤波器的尺寸增量也相应地增大。因此,对每一个新的组(octave),滤波器尺寸的增量是加倍的(从6到12,再到24)。同时,寻找兴趣点时的采样间隔也可加倍。
由于经过放大之后,不同滤波器尺寸的比值保持一致,近似Gaussian微分的尺度也相应的放大。例如,我们27×27的滤波器相当于Gaussian微分下采样。另外,不同滤波器尺寸下Frobenius范数保持不变,它们已经被进行了相对于尺度的归一化[26]。
为了在图像空间和尺度空间上定位兴趣点,在3×3×3邻域内使用了非最大值抑制。Hessian矩阵特征值的最大值,在尺度和图像空间内,使用Brown提出的方法进行插值。在我们的方法中,尺度空间的插值尤其重要,因为每一个组中第一层的尺度差异相对较大。图2左图给出了一个使用‘Fast-Hessian’检测算子检测得到兴趣点的例子。

图2 左边:一幅太阳花图片的兴趣点检测结果。这种场景很清楚的展示了基于Hessian矩阵的检测方法的性质。中间:SURF使用的Haar小波类型。右边:Graffiti场景中不同尺度下的描述窗口。
4 SURF描述算子
与其他描述算子相比,SIFT性能明显更好[8]。它将粗略的位置信息(crudely localised information)与基于梯度分布的特征结合在一起,在去除由于尺度和空间变化造成的定位误差时,能得到良好的独特性。使用相对强度和梯度方向能减小光照度变化的影响。
本文提出的SURF描述算子基于相似的性质,但进一步降低复杂度。第一步是在兴趣点周围的一个圆形邻域内,建立一个可重复确定的方向。然后基于该方向建立一个矩形区域,从中提取出SURF的描述算子。下面将依次介绍这两个步骤。我们还提出了一个简化版本的描述算子(U-SURF),它不具有旋转不变性,因此计算速度更快,更加适用于照相机基本保持水平的场合。
4.1 方向确定(Orientation Assignment)
为了做到旋转不变性,我们给兴趣点定义一个可重复的主方向。为了达到这个目的,我们首先计算x和y方向的Haar小波响应,如图2所示,这是在兴趣点周围半径6s的圆形邻域内进行的,s是该兴趣点的尺度。采样间隔也与尺度相关联,选为s。同样的,计算小波响应时也是和当前尺度有关,也被选为s。大尺度下小波的尺度也相应地增大。因此,我们又一次使用积分图像以实现快速滤波。任何尺寸下只需要六步计算,就可得到x或y方向的小波响应。小波的边长(side length)是4s。
计算出小波响应后,使用中心在兴趣点的高斯函数()进行加权,响应用一个向量来表示,水平方向响应沿着横坐标,垂直方向响应沿着纵坐标。主方向的确定方法是,计算一个60°角的旋转扇形窗口内响应的总和。对窗口内水平和垂直方向的小波响应分别进行求和。这两个加和响应构成一个新的向量。这种向量中最长的代表该兴趣点的方向。滑动窗口的尺寸是一个参数,通过实验的方法进行选择。尺寸过小在单个主小波响应时会失败,尺寸过大得到向量长度的最大值是不典型的。两种情况下兴趣区的方向都会不稳定。需要注意的是U-SURF省略了这个步骤。
4.2 描述分量(Deor Components)
为了得到描述向量,第一步是在兴趣点周围以其为中心建立一个矩形区域,方向沿着上文得到的兴趣点的主方向。对于upright版本,这种转换是不需要的。矩形区域的边长是20s,图2给出了这种矩形区域的例子。
把矩形区域规则地分解为4×4个小的子区域,子区域中保留重要的空间信息。对于每一个子区域,我们在规则的5×5的空间采样点上计算一些简单的特征。为简单起见,用dx表示在水平方向的Haar小波响应,用dy表示垂直方向的响应(滤波器的尺寸是2s)。这里的水平和垂直是根据上文选择的兴趣点的主方向定义的。
为了增加对几何变形和定位误差的鲁棒性,dx和dy首先会用一个中心在兴趣点的高斯函数()进行加权。
然后,小波响应dx和dy在每一个子区域内进行加和,形成了特征向量的第一个集合。为了考虑图像强度变化的极性(方向),我们也计算响应量的绝对值|dx|与|dy|的加和。因此,每一个子区域内用一个四维的描述向量v来描述其强度变化模式,。所有的4×4个子区域内的描述向量组合在一起构成了64维描述向量。小波响应对光照的变化(偏移)是不变的。将描述向量归一化为单位向量可以实现对比度不变。
图3给出了三种完全不同的图像强度模式下,子区域内描述算子的特性。可以将这种局部的强度模式进行组合,得到各种特殊的描述算子。
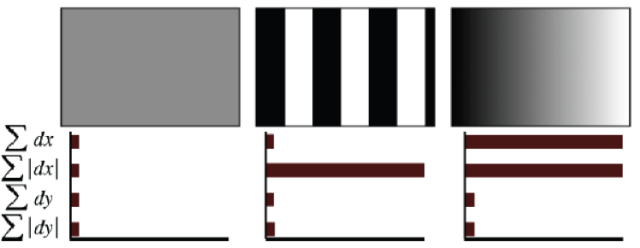
图3 几种子区域描述算子的类型,代表基本的亮度模式的性质。左边:表示区域内灰度值相近的情况,四个值都相对较低。中间:表示x方向的频率变化,的值较大,其余的值都很小。右边:x方向的强度逐渐增加,和的值都很大。
为了得到SURF的描述算子,我们实验了使用较少和较多的小波特征的方法,如使用dx⊃2;和dy⊃2;,高阶小波变换,PCA,中值,均值等等。通过全面的评估,发现上文给出的方法性能最好。然后我们又改变采样点和子区域的数目。4×4的子区域分割方法被证实是最好的。因为更细小的划分会降低鲁棒性,并且会显著增加匹配的时间。另一方面,使用3×3的子区域得到的较低维的描述向量(SURF-36)性能较差,但是匹配的速度快,与文献中其他的描述算子相比仍然是可接受的。图4给出了一小部分比较结果(SURF-128在下文有简单介绍)。

图4 recall vs. 1-precision曲线图,不同的binning方法及两种不同的匹配技术,测试的图像序列是‘Graffiti’(第1和第3幅图),两幅图有30度的视角变化,与现有描述算子进行比较。这些兴趣点都是使用我们的’Fast Henssian’检测算子得到的。需要注意,兴趣点不是仿射不变的,因此图中的结果与[8]中的结果没有可比性。SURF-128表示扩展版本的描述算子。左边:基于相似度阈值的匹配技术,右边:基于最近邻比率的匹配策略(见第5部分)。
我们也测试了另一个版本的SURF描述算子,增加了一些与之前类似的特征(SURF-128)。它仍然使用了与之前相同的加和,但是进一步对这些加和进行分解。dx和|dx|的加和根据dy<0和dy≥0分成两部分进行计算。类似的,dy和|dy|根据dx的符合分开进行加和,因此描述特征的数量加倍。这种描述算子独特性更好,并且计算速度不会慢很多,但是因为维度的增加,匹配时速度会慢很多。
图4中,基于标准的‘Graffiti’场景比较参数的选择,‘Graffiti’是标准评估数据集Mikolajczyk[8]中最具挑战性的场景,由于它包含了平面外的转动、平面内的转动以及亮度的变化。4×4子区域的扩展版本SURF-128表现最好。SURF性能好且计算速度更快,这两方面都比现有的描述算子优秀。
在匹配阶段为了快速索引,兴趣点的Laplacian的符号(即Hessian矩阵的迹)可以考虑进来。通常兴趣点在斑点状的结构附近发现。Laplacian的符号可以区分亮的斑点暗的背景和它的相反情况(即暗的斑点亮的背景)。Laplacian的符号不需要花费额外的计算量,因为在检测阶段已经计算得到。在匹配阶段,我们仅匹配具有相同类型对比度的特征(即Laplacian符号相同的特征点)。因此,这个简单的信息可以加快匹配的速度,对算法的性能有稍微的提升。
5 实验结果
首先我们给出基于一个标准数据集的实验结果,来评估检测和描述算子。然后讨论应用于现实生活中物体识别的实验结果。所有参与比较的检测和描述算子都是作者之前实现的。
标准数据集 我们使用Mikolajczyk[1]提供的图像序列和测试软件,来测试自己的检测和描述算子。这是一些有纹理和结构的现实场景的照片。由于篇幅的限制,我们不会介绍对所有图像序列的实验结果。对于检测算子的比较,我们选择两个视角变化的序列(Graffiti和Wall),一个缩放和旋转变化序列(Boat),光线变化序列(Leuven)(分析结果将在下文Fig.6中进行讨论)。描述算子作用于除Bark外的所有序列(图4和图7)。
在评价检测算子时,我们使用[9]中提出的可重复分数做为指标。这个指标的意义是,两幅图像中都能检测到的兴趣点的数目,与总共能检测到的最少兴趣点的数目的比值(只考虑在两幅图像中都可见的兴趣点)。
作为比较的检测算子包括Lowe[2]的高斯差分检测算子(DoG)、Mikolajczyk[15]提出的Harris-Laplace和Hessian-Laplace算子。平均意义上来说,所有检测算子检测到的兴趣点数目相当。这个结论适用于所用的图像,包括在物体识别实验中要到的数据库中的图像,表1给出一个示例。可以看出我们的Fast-Hessian检测器计算速度比DOG快三倍,比Hessian-Laplace快5倍。同时,对Graffiti、Leuven和Boats图像序列,我们检测器的重复率与对比算法差不多,针对Wall图像序列重复率甚至更好。需要注意的是Graffiti和Wall图像序列,包括了平面外的旋转,导致了仿射变形,然而参与比较的检测算子都只具有旋转和尺度不变性。因此,为了应对仿射变形,必须提高检测算子整体的鲁棒性。

表1 阈值,检测到的兴趣点的数目,检测花费的计算时间(使用Graffiti场景的第一幅图像,分辨率800×640)
描述算子用recall-(1-precision)曲线图来评价,与文献[4]和[8]类似。每次评价,我们使用图像序列中的第1和第4幅图像,但是有两个例外:Graffiti序列使用第1和第3幅图像,它们有30°的视角变化;Wall序列使用第1和第5幅图像,它们有50°的视角变化。在图4和图7中,比较了我们的SURF描述算子与GLOH、SIFT、PCA-SIFT的性能差异,都是基于我们的‘Fast-Hessian’检测算子得到的兴趣点。几乎在所有的比较中,SURF的表现都优于其他的描述算子。图4给出了使用两种不同匹配技术的比较结果,一个是基于相似度阈值,一个是基于最近邻比率(这两种的技术的介绍参见文献[8])。匹配技术对检测器优劣的排名没有影响,SURF在两种情形下都是最好的。由于篇幅的限制,仅在图7中给出基于相似度阈值匹配技术的实验结果,因为这种技术更加适合表达检测算子在其特征空间的分布情况,并且使用的更加广泛。
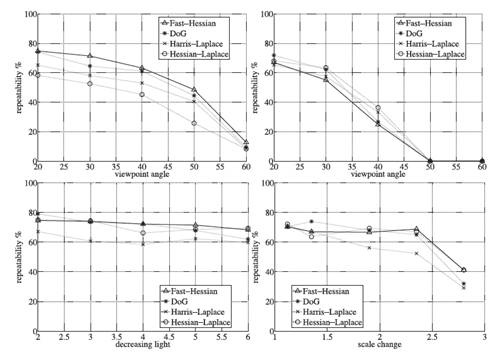
图6 不同图像序列的可重复率的分数,从左到右,从上到下,分别是Wall和Graffiti(视角变化),Leuven(亮度变化),Boat(缩放和旋转)。
SUFT描述算子性能完全优于其他,有时对同样精度的图形进行检索,甚至会有10%的性能提升。同时计算速度很快,如表2所示。第4部分介绍的精确版本的描述算子SURF-128,结果比常规的SURF效果稍好,但是匹配的速度要慢一些,因此在依赖计算速度的应用场景不太适用。

表2 检测-描述花费的总时间,测试图像是Graffiti序列的第一幅图像。阈值是可自适应调整的,以保证所有方法检测到的兴趣点数目相同。表中的相对速度对其他图像也具有代表性。
需要指出的是,整篇文章中,包括下文物体识别的实验,我们都使用相同的参数和阈值(如表1所示)。文中给出的计算时间都是基于标准的Linux PC(Pentium IV,3GHz)。
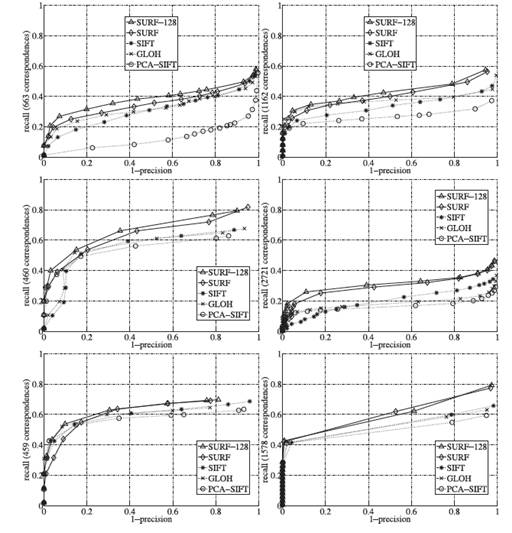
图7 Recall-(1-Precision)的曲线图,从左到右,从上到下,分别是50度的视角变化(Wall),放大2倍(Boat),图像模糊(Bikes和Trees),亮度变化(Leuven),JPEG压缩(Ubc)。
物体识别 我们也在一个实际的应用场景下测试算法的特性,目标是在一个博物馆里进行物体的识别。这个数据库包含216幅照片,22个物体。这216幅照片在不同的条件下拍摄,包括极端的光照变化、物体位于反光玻璃罩内、视角变化、缩放、不同的相机质量等。此外,照片的尺寸较小(320×240),因此给识别增加了难度,因为丢失了很多细节。
为了在数据库中进行物体识别,我们按照如下流程进行。测试集的图像与参考集中所有图像进行比较,比较它们各自的兴趣点。参考数据集中与测试数据集,兴趣点匹配数目最多的物体被认为是识别出来的物体。
匹配过程如下。测试数据集中的一个兴趣点与参考数据集中的一个兴趣点进行比较,计算它们描述向量的Euclidean距离。当它们之间的距离小于0.7倍的第二近的距离时,认为检测出一个匹配对。这就是最近邻比率匹配策略[18,2,7]。很显然,附加的几何约束可以减小错误的正向匹配的影响,并且可以用于在任何的匹配策略。然而对比较问题而言,几何约束没有意义,因为可能会掩盖掉基础算法的某些缺陷。平均识别率反映了算法性能比较的结果。表现最好的是SURF-128,识别率为85.7%;然后是U-SURF(83.8%),SURF(82.6%)。其他的描述算子识别率分别为78.3%(GLOH),78.1%(SIFT),72.3%(PCA-SIFT)。

图5 给出一个例子,左侧是参考图像,右侧是测试图像,注意观察两者在视角和颜色上的不同。
6 结论
本文提出了一种快速且性能良好的兴趣点检测和描述算法,在计算速度和准确性方面都优于目前存在的算法。描述算子很容易扩展为仿射不变性。接下来的工作是优化代码,进一步提高运算速度。最新的版本可在网上找到[1]。
参考文献
(蓝色区域滑动浏览全部文献)
1. Lindeberg, T.: Feature detection with automatic scale selection. IJCV 30(2)
(1998) 79 – 116
2. Lowe, D.: Distinctive image features from scale-invariant keypoints, cascade filter-
ing approach. IJCV 60 (2004) 91 – 110
3. Mikolajczyk, K., Schmid, C.: An affine invariant interest point detector. In: ECCV.
(2002) 128 – 142
4. Ke, Y., Sukthankar, R.: PCA-SIFT: A more distinctive representation for local
image deors. In: CVPR (2). (2004) 506 – 513
5. Tuytelaars, T., Van Gool, L.: Wide baseline stereo based on local, affinely invariant
regions. In: BMVC. (2000) 412 – 422
6. Matas, J., Chum, O., M., U., Pajdla, T.: Robust wide baseline stereo from maxi-
mally stable extremal regions. In: BMVC. (2002) 384 – 393
7. Mikolajczyk, K., Schmid, C.: A performance evaluation of local deors. In:
CVPR. Volume 2. (2003) 257 – 263
8. Mikolajczyk, K., Schmid, C.: A performance evaluation of local deors. PAMI
27 (2005) 1615–1630
9. Mikolajczyk, K., Tuytelaars, T., Schmid, C., Zisserman, A., Matas, J., Schaffal-
itzky, F., Kadir, T., Van Gool, L.: A comparison of affine region detectors. IJCV
65 (2005) 43–72
10. Harris, C., Stephens, M.: A combined corner and edge detector. In: Proceedings
of the Alvey Vision Conference. (1988) 147 – 151
11. Mikolajczyk, K., Schmid, C.: Indexing based on scale invariant interest points. In:
ICCV. Volume 1. (2001) 525 – 531
12. Lowe, D.: Object recognition from local scale-invariant features. In: ICCV. (1999)
13. Kadir, T., Brady, M.: Scale, saliency and image deion. IJCV 45(2) (2001)
83 – 105
14. Jurie, F., Schmid, C.: Scale-invariant shape features for recognition of object
categories. In: CVPR. Volume II. (2004) 90 – 96
15. Mikolajczyk, K., Schmid, C.: Scale and affine invariant interest point detectors.
IJCV 60 (2004) 63 – 86
16. Florack, L.M.J., Haar Romeny, B.M.t., Koenderink, J.J., Viergever, M.A.: General
intensity transformations and differential invariants. JMIV 4 (1994) 171–187
17. Mindru, F., Tuytelaars, T., Van Gool, L., Moons, T.: Moment invariants for recog-
nition under changing viewpoint and illumination. CVIU 94 (2004) 3–27
18. Baumberg, A.: Reliable feature matching across widely separated views. In: CVPR.
(2000) 774 – 781
19. Schaffalitzky, F., Zisserman, A.: Multi-view matching for unordered image sets, or
“How do I organize my holiday snaps?”. In: ECCV. Volume 1. (2002) 414 – 431
20. Freeman, W.T., Adelson, E.H.: The design and use of steerable filters. PAMI 13
(1991) 891 – 906
21. Carneiro, G., Jepson, A.: Multi-scale phase-based local features. In: CVPR (1).
(2003) 736 – 743
22. Se, S., Ng, H., Jasiobedzki, P., Moyung, T.: Vision based modeling and localiza-
tion for planetary exploration rovers. Proceedings of International Astronautical
Congress (2004)
23. Viola, P., Jones, M.: Rapid object detection using a boosted cascade of simple
features. In: CVPR (1). (2001) 511 – 518
24. Koenderink, J.: The structure of images. Biological Cybernetics 50 (1984) 363 –
370
25. Lindeberg, T.: Discrete Scale-Space Theory and the Scale-Space Primal Sketch,
PhD, KTH Stockholm,. KTH (1991)
26. Lindeberg, T., Bretzner, L.: Real-time scale selection in hybrid multi-scale repre-
sentations. In: Scale-Space. (2003) 148–163
27. Brown, M., Lowe, D.: Invariant features from interest point groups. In: BMVC.
(2002)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号