P7475 「C.E.L.U-02」简易输入法 题解

这么好的题竟然没人写 FHQ，我来补上。

前置知识：Trie，FHQ_Treap。

思路

我们知道，若 Trie 上从根到 $x$ 的路径表示字符串 $s$，

则以 $x$ 为根的子树可以表示有前缀 $s$ 的字符串的集合。

举个例子，样例 2：

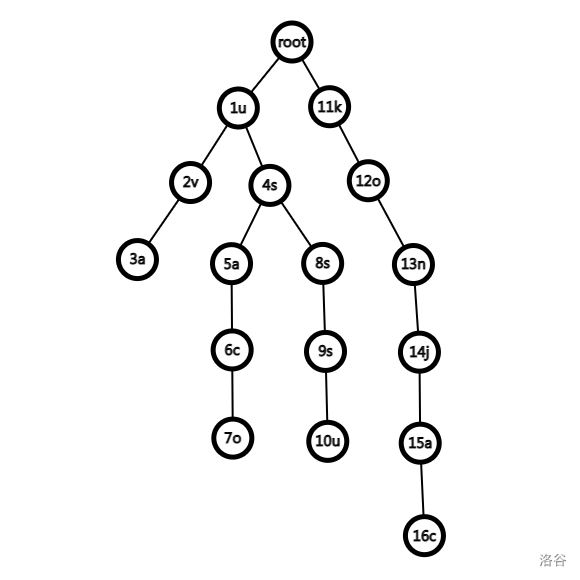
以 $\text{1u}$ 为根的子树可以表示有前缀 $\text{u}$ 的字符串的集合 $\{\text{usa},\text{usaco},\text{usssu},\text{uva}\}$，

以 $\text{4s}$ 为根的子树可以表示有前缀 $\text{us}$ 的字符串的集合 $\{\text{usa},\text{usaco},\text{usssu}\}$，

以 $\text{5a}$ 为根的子树可以表示有前缀 $\text{usa}$ 的字符串的集合 $\{\text{usa},\text{usaco}\}$，其他节点以此类推。

所以，对于每次询问 $s$，在 Trie 上找到有前缀 $s$ 的字符串的集合，

答案即为集合中以输出次数降序为第一关键字，以字典序升序为第二关键字的第 $x$ 大。

每次询问后将输出的字符串出现次数加一，更新所有包含这个字符串的集合。

用平衡树维护每个节点上的集合即可。

有 $O(n|s|)$ 个集合，插入操作复杂度为 $O(|s|\log n)$，

所有询问要访问 $O(m|s|)$ 个集合，查询与更新复杂度为 $O(|s|\log n)$，

则总复杂度为 $O((n+m)|s{|}^2\log n)$，可以过掉。

代码

比大部分 Splay 短一半，快 1s。

#include <string>
#include <cstdlib>
#include <iostream>
using namespace std;
int n, m, z, x;string s, q;
struct P
{
    int x;string s;inline P operator++() {return P{x, s + '\0'};}
    inline bool operator<(P p) {return x == p.x ? s < p.s : x > p.x;}
}p;
struct F
{
    F *l, *r;P v;int k, s;
    inline F(P _) : l(0), r(0), v(_), k(rand()), s(1) {}
    inline void p() {s = 1;if(l) s += l->s;if(r) s += r->s;}
}*a, *b, *c;
void S(F *x, P v, F *&a, F *&b)
{
    if(!x) {a = b = 0;return;}
    if(x->v < v) a = x, S(x->r, v, a->r, b), a->p();
    else b = x, S(x->l, v, a, b->l), b->p();
}
F *M(F *a, F *b)
{
    if(!a) return b;if(!b) return a;
    if(a->k < b->k) {a->r = M(a->r, b);a->p();return a;}
    else {b->l = M(a, b->l);b->p();return b;}
}
struct T
{
    T *d[26];F *r = 0;
    inline void I(P v) {S(r, v, a, b);r = M(a, M(new F(v), b));}
    inline void D(P v) {S(r, v, a, b);S(b, ++v, b, c);r = M(a, c);delete b;}
    inline P K(int k)
    {
        a = r;k = min(k, a->s);while(1)
        {
            z = a->l ? a->l->s : 0;if(k == z + 1) return a->v;
            if(k <= z) a = a->l;else k -= z + 1, a = a->r; 
        }
    }
}*r = new T(), *t;
int main()
{
    ios::sync_with_stdio(0);cin.tie();cout.tie();
    srand(388651);cin >> n;while(n--)
    {
        cin >> s;t = r;for(int i = 0;i < s.length();++i)
            (t = t->d[x = s[i] - 'a'] ? t->d[x] : t->d[x] = new T())->I(P{0, s});
    }
    cin >> m;while(m--)
    {
        cin >> s >> z;t = r;for(int i = 0;i < s.length();++i)
            if(!(t = t->d[s[i] - 'a'])) {cout << "404Error" << endl;break;}
        if(!t) continue;cout << (q = (p = t->K(z)).s) << endl;
        x = p.x;t = r;for(int i = 0;i < q.length();++i)
            (t = t->d[q[i] - 'a'])->D(p), t->I(P{x + 1, q});
    }
    return 0;
}

注意 struct P 中重载 operator++ 处理删除操作的技巧。

小优化

实际上，每个节点的字符串集合中，字符串有公共前缀。

我们可以把这个公共前缀省掉，只存每个字符串的后缀。

但实际优化效果并不明显（应该是写丑了），给出参考代码：

#include <string>
#include <cstdlib>
#include <iostream>
using namespace std;
int n, m, z, x;string s, q;
struct P
{
    int x;string s;inline P operator++() {return P{x, s + '\0'};}
    inline bool operator<(P p) {return x == p.x ? s < p.s : x > p.x;}
}p;
struct F
{
    F *l, *r;P v;int k, s;
    inline F(P _) : l(0), r(0), v(_), k(rand()), s(1) {}
    inline void p() {s = 1;if(l) s += l->s;if(r) s += r->s;}
}*a, *b, *c;
void S(F *x, P v, F *&a, F *&b)
{
    if(!x) {a = b = 0;return;}
    if(x->v < v) a = x, S(x->r, v, a->r, b), a->p();
    else b = x, S(x->l, v, a, b->l), b->p();
}
F *M(F *a, F *b)
{
    if(!a) return b;if(!b) return a;
    if(a->k < b->k) {a->r = M(a->r, b);a->p();return a;}
    else {b->l = M(a, b->l);b->p();return b;}
}
struct T
{
    T *d[26];F *r = 0;
    inline void I(P v) {S(r, v, a, b);r = M(a, M(new F(v), b));}
    inline void D(P v) {S(r, v, a, b);S(b, ++v, b, c);r = M(a, c);delete b;}
    inline P K(int k)
    {
        a = r;k = min(k, a->s);while(1)
        {
            z = a->l ? a->l->s : 0;if(k == z + 1) return a->v;
            if(k <= z) a = a->l;else k -= z + 1, a = a->r; 
        }
    }
}*r = new T(), *t;
int main()
{
    ios::sync_with_stdio(0);cin.tie();cout.tie();
    srand(388651);cin >> n;while(n--)
    {
        cin >> s;t = r;for(auto i = s.begin(), l = s.end();i != l;++i)
            (t = t->d[x = *i - 'a'] ? t->d[x] : t->d[x] = new T())->I(P{0, string(i + 1, l)});
    }
    cin >> m;while(m--)
    {
        cin >> s >> z;t = r;for(int i = 0;i < s.length();++i)
            if(!(t = t->d[s[i] - 'a'])) {cout << "404Error" << endl;break;}
        if(!t) continue;cout << (s += (q = (p = t->K(z)).s)) << endl;
        x = p.x;t = r;for(auto i = s.begin(), l = s.end();i != l;++i)
            q = string(i + 1, l), (t = t->d[*i - 'a'])->D(P{x, q}), t->I(P{x + 1, q});
    }
    return 0;
}