P2127 序列排序 题解

你们代码都好长啊.jpg

题意

给定无相等元素的 $\{a_n\}$，交换 $a_x,a_y$ 的代价为 $a_x+a_y$，求将 $\{a_n\}$ 升序排序的最小代价。

思路

注意到 $\{a_n\}$ 中不存在相等元素，即可以确定 $a_i$ 排序后的位置。

我们记 $p_i$ 为 $a_i$ 排序后的位置，可以用离散化求出 $\{p_n\}$。

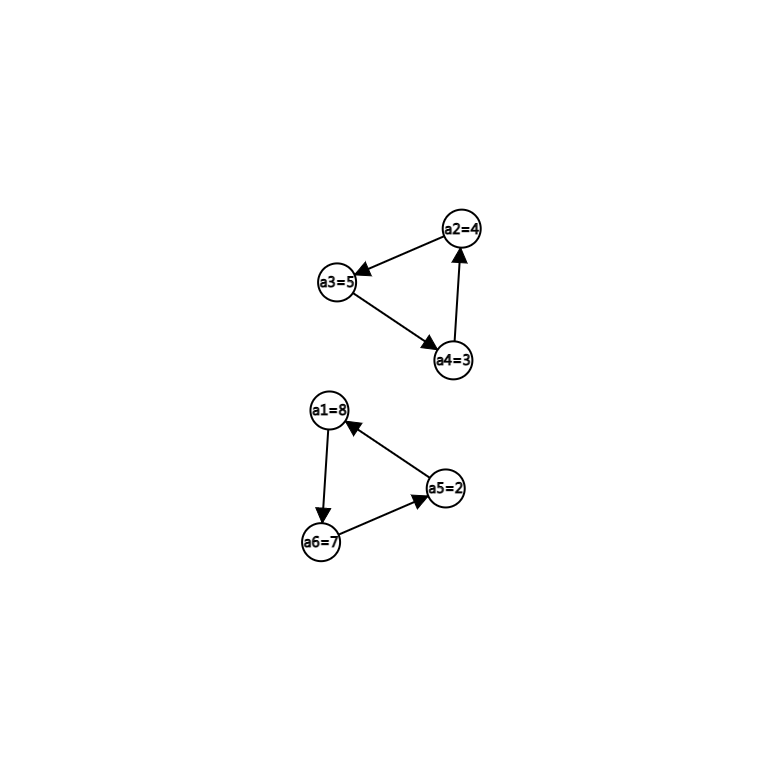
容易发现，如果 $i$ 向 $p_i$ 连有向边，可以形成若干个环。（图为样例）

一个比较显然的贪心：选出每个环中的最小值，与其他点依次交换。

若某个环的点数为 $r$，点权和为 $s$，最小值为 $m$，则此环总代价为 $s+m(r-2)$。

注意到可以先将环中最小值与全局最小值交换，再与其他点依次交换，最后把全局最小值与环中最小值换回来。

若全局最小值为 $M$，则此环总代价为 $s+m+M(r+1)$。

取两种方案的最小值，答案为 $\sum\min\{s+m(r-2),s+m+M(r+1)\}$。

代码

#include <cstdio>
#include <algorithm>
#define F for(int i = 0;i < n;++i)
using namespace std;
int n, m, M = 1e9, a[100050], f[100050], p[100050];long long r, s, q;bool v[100050];
void D(int x) {if(v[x]) return;v[x] = 1;++r;s += a[x];m = min(m, a[x]);D(p[x]);}
int main()
{
    scanf("%d", &n);F scanf("%d", a + i), M = min(M, f[i] = a[i]);
    sort(f, f + n);F p[i] = lower_bound(f, f + n, a[i]) - f;F if(!v[i])
    r = s = 0, m = 1e9, D(i), q += s + min(m * (r - 2), m + M * (r + 1));
    return printf("%lld", q), 0;
}