8.21 模拟赛简明题解

A

题意：给定一个环形数列，维护区间加，区间最小值。

线段树板题，不解释。题外话：A 题码量最大

#include <cstdio>
#include <algorithm>
#define G int m = s + t >> 1
using namespace std;
struct T
{
    T *l, *r;long long v, x;T() : l(0), r(0), v(0), x(0) {}void u() {v =
    min(l->v, r->v);}void d() {if(x) l->v += x, r->v += x, l->x += x, r->x += x, x = 0;}
}*r;
void B(int s, int t, T *&p)
{
    p = new T();if(s == t) {scanf("%lld", &p->v);
    return;}G;B(s, m, p->l);B(m + 1, t, p->r);p->u();
}
void M(int l, int r, long long x, int s, int t, T *p)
{
    if(l <= s && t <= r) {p->v += x;p->x += x;return;}p->d();G;if(l <= m)
    M(l, r, x, s, m, p->l);if(r > m) M(l, r, x, m + 1, t, p->r);p->u();
}
long long Q(int l, int r, int s, int t, T *p)
{
    if(l <= s && t <= r) return p->v;p->d();G;long long q = 1e18;if(l <= m) q =
    min(q, Q(l, r, s, m, p->l));if(r > m) q = min(q, Q(l, r, m + 1, t, p->r));return q;
}
int n, m, x, y;long long k;
int main()
{
    scanf("%d", &n);B(1, n, r);scanf("%d", &m);while(m--)
    {
        scanf("%d%d", &x, &y);++x;++y;if(getchar() != '\n')
        {
            scanf("%lld", &k);if(x <= y) M(x, y, k, 1, n, r);
            else M(x, n, k, 1, n, r), M(1, y, k, 1, n, r);
        }
        else
        {
            if(x <= y) printf("%lld\n", Q(x, y, 1, n, r));
            else printf("%lld\n", min(Q(x, n, 1, n, r), Q(1, y, 1, n, r)));
        }
    }
    return 0;
}

B

题意：给定字符串 $S|S_i\in\{A,B,C\}$，定义 $S^0=S$，$S^i|i>0$ 为对 $S^{i-1}$ 执行 $A\to BC,B\to CA,C\to AB$ 的结果，$Q$ 次询问 $S^t_k$。

考虑把 $S^t$ 分成 $|S|$ 个长度为 $2^t$ 的子串。不难发现 $S^t_k$ 属于 $S^t$ 的第 $\lceil\dfrac k{2^t}\rceil$ 个子串，即 $S^t_k$ 由 $S_{\lceil\frac k{2^t}\rceil}$ 变化而来。

注意到 $S_{\lceil\frac k{2^t}\rceil}$ 变成 $S^t_k$ 的过程是一棵二叉树。

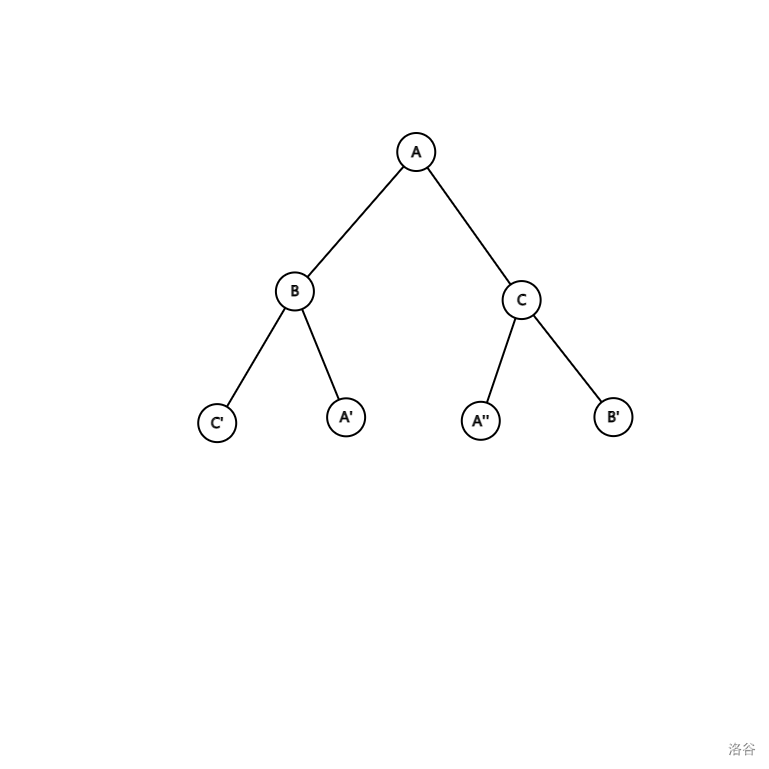
记 $l_i$ 为 $i$ 的左孩子，$r_i$ 为 $i$ 的右孩子。考虑 $i$ 与 $l_i,r_i$ 的关系。

记 $T=\text{ABCABCABC......}$，若 $i=T_x$，则 $l_i=T_{x+1},r_i=T_{x+2}$。

注意到 $S^t_k$ 的父亲是 $S^{t-1}_{\lceil\frac k2\rceil}$。也就是说，若 $S^{t-1}_{\lceil\frac k2\rceil}=T_x$，则

$$ S^t_k=\begin{cases}T_{x+1}&S^t_k=l_{S^{t-1}_{\lceil\frac k2\rceil}}(\text{即}k\bmod 2=1)\\T_{x+2}&S^t_k=r_{S^{t-1}_{\lceil\frac k2\rceil}}(\text{即}k\bmod 2=0)\end{cases} $$

考虑从 $S^t_k$ 向上爬树，记录路径上点的贡献。

注意 $k=1$ 时路径上的点都为其父亲的左孩子，此时无须继续爬树，因为之后每层贡献都为 $1$。

#include <cstdio>
#include <cstring>
int Q, p, q;long long t, k, l;char s[100050];
int main()
{
    scanf("%s%d", s + 1, &Q);while(Q--)
    {
        scanf("%lld%lld", &t, &k);l = 1;p = 0;
        for(int i = 0;i < t;++i) if((l <<= 1) >= k) {p = 1;break;}
        if(p != 1) p = (k + l - 1) / l;k = (k - 1) % l + 1;q = 0;
        while(k != 1) {if(k & 1) ++q;else q += 2;k = k + 1 >> 1;--t;}
        putchar((s[p] + q + t - 'A') % 3 + 'A');puts("");
    }
    return 0;
}

C

题意：给定序列 $\{a_n\},\{b_n\}$，求 $\sum\limits_{l=1}^n\sum\limits_{r=l}^n[\max\limits_{i=l}^ra_i=\min\limits_{i=l}^rb_i]$。

注意到最值具有单调性，$[\max\limits_{i=l}^ra_i\geq\min\limits_{i=l}^rb_i]$ 与 $[\max\limits_{i=l}^ra_i>\min\limits_{i=l}^rb_i]$ 同样具有单调性。

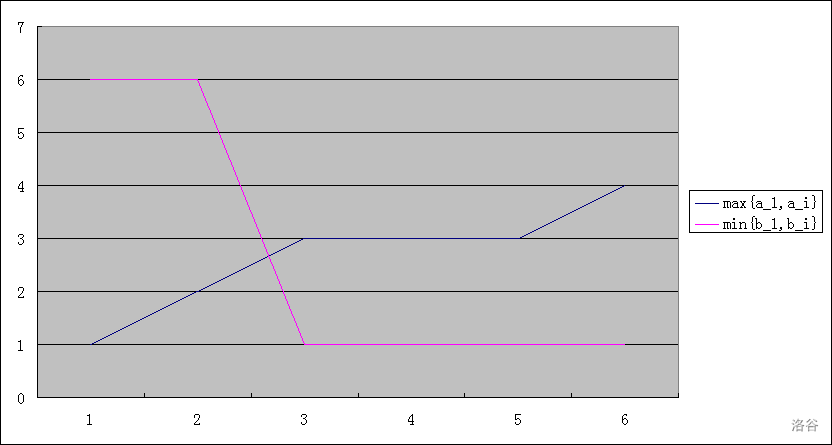
考虑枚举 $l$，二分出满足 $\max\limits_{i=l}^xa_i\geq\min\limits_{i=l}^xb_i$ 的最小 $x$ 和满足 $\max\limits_{i=l}^ya_i>\min\limits_{i=l}^yb_i$ 的最小 $y$，则 $r\in[x,y-1]$ 均符合要求。

考虑用 ST 表维护区间最值。

#include <cstdio>
#include <algorithm>
using namespace std;
int n, l[200050], a[20][200050], b[20][200050];long long q;
int Q(int x, int y) {int k = l[y - x + 1];return max(a[k][x],
a[k][y - (1 << k) + 1]) - min(b[k][x], b[k][y - (1 << k) + 1]);}
int main()
{
    scanf("%d", &n);
    for(int i = 2;i <= n;++i) l[i] = l[i >> 1] + 1;
    for(int i = 1;i <= n;++i) scanf("%d", &a[0][i]);
    for(int i = 1;i <= n;++i) scanf("%d", &b[0][i]);
    for(int i = 1;1 << i <= n;++i)
        for(int j = 1;j + (1 << i) - 1 <= n;++j)
            a[i][j] = max(a[i - 1][j], a[i - 1][j + (1 << i - 1)]),
            b[i][j] = min(b[i - 1][j], b[i - 1][j + (1 << i - 1)]);
    for(int i = 1, l, r, m, x, y;i <= n;++i, q += y - x)
    {
        for(l = i, r = n, x = n + 1;l <= r;) if(Q(i, m =
        l + r >> 1) >= 0) x = m, r = m - 1;else l = m + 1;
        for(l = i, r = n, y = n + 1;l <= r;) if(Q(i, m =
        l + r >> 1) > 0) y = m, r = m - 1;else l = m + 1;
    }
    return printf("%lld", q), 0;
}

D

题意：给定序列 $\{a_n\},\{b_k\}$，求有多少个 $\{a_n\}$ 的排列 $\{p_n\}$ 满足 $\forall x,y,\sum\limits_{i=1}^xa_i\neq b_y$。

注意到数据范围很小，考虑状压 dp。设 $f_S$ 为已选数集合为 $S$ 时的方案数，$s_S$ 为 $\sum\limits_{i\in S}a_i$。显然有：

$$ f_S=\begin{cases}0&\exists j,s_S=b_j\\\sum\limits_{i\in S}f_{S-i}&\forall j,s_S\neq b_j\end{cases} $$

无须预处理 $s_S$，可以状态转移时更新 $s_S=s_{S-\operatorname{lowbit}(S)}+s_{\operatorname{lowbit}(S)}$。

枚举 $i\in S$ 时，可以令 $T=S$，不断令 $T\gets T-\operatorname{lowbit}(T)$，每次减的 $\operatorname{lowbit}(T)$ 即为要枚举的 $i$。

#include <cstdio>
int n, k, u, b[2], s[20000050], f[20000050];
int main()
{
    scanf("%d", &n);for(int i = 0;i < n;++i) scanf("%d", s + (1 << i));
    scanf("%d", &k);for(int i = 0;i < k;++i) scanf("%d", b + i);f[0] = 1;
    for(int i = 1, u = 1 << n;i < u;++i)
    {
        s[i] = s[i & i - 1] + s[i & -i];if(s[i] != b[0] && s[i] != b[1])
        for(int j = i;j;j &= j - 1) (f[i] += f[i ^ (j & -j)]) %= 1000000007;
    }
    return printf("%d", f[(1 << n) - 1]), 0;
}

（用 i & i - 1 计算 $i-\operatorname{lowbit}(i)$，i & -i 计算 $\operatorname{lowbit}(i)$）

---

鉴于多人反映码风问题，贴一下 Isaac_Chou 的 Code。

思路完全一致，请放心食用。

//A
#include <bits/stdc++.h>
#define int long long
#define inf 2147483647
using namespace std;
const int N = 2e5 + 5;
int n, a[N], lazy[N << 2], mn[N << 2], m; string line;
int ls (int k) {return (k << 1);}
int rs (int k) {return (k << 1 | 1);}
void pushup (int k) {mn[k] = min(mn[ls(k)], mn[rs(k)]);}
void pushdown (int k) {
    if (lazy[k]) {
        lazy[ls(k)] += lazy[k]; lazy[rs(k)] += lazy[k];
        mn[ls(k)] += lazy[k]; mn[rs(k)] += lazy[k];
        lazy[k] = 0;
    }
}
void build (int l, int r, int k) {
    if (l == r) {
        mn[k] = a[l];
        return ;
    }
    int mid = (l + r) >> 1;
    build (l, mid, ls(k));
    build (mid + 1, r, rs(k));
    pushup (k);
}
void modify (int L, int R, int v, int l, int r, int k) {
    if (L <= l and r <= R) {
        lazy[k] += v;
        mn[k] += v;
        return ;
    }
    int mid = (l + r) >> 1;
    pushdown (k);
    if (L <= mid) modify (L, R, v, l, mid, ls(k));
    if (R >  mid) modify (L, R, v, mid + 1, r, rs(k));
    pushup (k);
}
int query (int L, int R, int l, int r, int k) {
    if (L <= l and r <= R) return mn[k];
    int mid = (l + r) >> 1;
    pushdown (k);
    int ans = inf;
    if (L <= mid) ans = min (ans, query(L, R, l, mid, ls(k)));
    if (R >  mid) ans = min (ans, query(L, R, mid + 1, r, rs(k)));
    return ans;
}
signed main () {
    scanf ("%lld", &n);
    for (int i = 1; i <= n; ++ i) scanf ("%lld", &a[i]);
    build (1, n, 1);
    scanf ("%lld", &m);
    getline (cin, line);
    for (int i = 1; i <= m; ++ i) {
        int x = 0, y = 0, v = 0, cnt = 0; string s;
        scanf ("%lld%lld", &x, &y);
        x ++; y ++;
        if (x <= y) {
            if (getchar() != '\n') {
                scanf ("%lld", &v);
                modify (x, y, v, 1, n, 1);
            }
            else printf ("%lld\n", query(x, y, 1, n, 1));
        }
        else {
            if (getchar() != '\n') {
                scanf ("%lld", &v);
                modify (x, n, v, 1, n, 1);
                modify (1, y, v, 1, n, 1);
            }
            else {
                int ans1 = query(x, n, 1, n, 1);
                int ans2 = query(1, y, 1, n, 1);
                printf ("%lld\n", min (ans1, ans2));
            }
        }
    }
    fclose(stdin);
    fclose(stdout);
    return 0;
}

//B
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 5;
char s[N];
int q, t, k, a[N];
signed main () {
    scanf ("%s", s + 1);
    int n = strlen (s + 1);
    for (int i = 1; i <= n; ++ i) a[i] = (s[i] - 'A');
    scanf ("%lld", &q);
    while (q --) {
        int len = 1, pos = 0, tmp = 0;
        scanf ("%lld%lld", &t, &k);
        for (int i = 1; i <= t; ++ i) {
            len *= 2;
            if (k <= len) {
                pos = 1;
                break;
            }
        }
        if (!pos) {
            pos = (k + len - 1) / len;
            k = (k - 1) % len + 1;
        }
        while (k != 1) {
            if (k & 1) tmp += 1;
            else tmp += 2;
            t -= 1;
            k = (k + 1) / 2;
        }
        tmp += t; 
        printf ("%c\n", 'A' + (a[pos] + tmp) % 3);
    }
}

//C
#include <bits/stdc++.h>
#define int long long 
using namespace std;
const int N = 2e5 + 5;
int mx[N][22], mn[N][22], a[N], b[N], n, lg[N], ans;
int query(int flg, int l, int r) {
    int log = lg[r - l + 1];
    if (flg) return max(mx[l][log], mx[r - (1 << log) + 1][log]);
    else return min(mn[l][log], mn[r - (1 << log) + 1][log]);
}
bool check1 (int l, int now) {
    if (query(1, l, now) >= query(0, l, now)) return 1;
    return 0;
}
bool check2 (int l, int now) {
    if (query(1, l, now) > query(0, l, now)) return 1;
    return 0;
}
signed main () {
    scanf ("%lld", &n);
    for (int i = 2; i <= n; ++ i) lg[i] = lg[i / 2] + 1;
    for (int i = 1; i <= n; ++ i) scanf ("%lld", &mx[i][0]);
    for (int i = 1; i <= n; ++ i) scanf ("%lld", &mn[i][0]);
    for (int j = 1; j <= 21; ++ j) for (int i = 1; i + (1 << j) - 1 <= n; ++ i)
            mx[i][j] = max(mx[i][j - 1], mx[i + (1 << (j - 1))][j - 1]);
    for (int j = 1; j <= 21; ++ j) for (int i = 1; i + (1 << j) - 1 <= n; ++ i)
            mn[i][j] = min(mn[i][j - 1], mn[i + (1 << (j - 1))][j - 1]);        
    for (int l = 1; l <= n; ++ l) {
        int nl = l, nr = n, ans1, ans2;
        while (nr - nl >= 0) {
            int mid = (nl + nr) >> 1;
            if (check1(l, mid)) nr = mid - 1;
            else nl = mid + 1;
        }
        ans1 = nl;
        nl = l, nr = n;
        while (nr - nl >= 0) {
            int mid = (nl + nr) >> 1;
            if (check2(l, mid)) nr = mid - 1;
            else nl = mid + 1;
        }
        ans2 = nl;
        ans += ans2 - ans1;
    }
    printf ("%lld\n", ans);
}

//D
#include <bits/stdc++.h>
#define mod 1000000007
#define lowbit(x) (x&(-x))
using namespace std;
const int N = 25;
int n, a[1 << N], k, m[3], final, f[1 << N];
int main () {
    scanf ("%d", &n); final = (1 << n) - 1;
    for (int i = 1; i <= final; i <<= 1) scanf ("%d", &a[i]);
    scanf ("%d", &k);
    for (int i = 1; i <= k; ++ i) scanf ("%d", &m[i]);
    f[0] = 1;
    for (int i = 0; i <= final; ++ i) {
        a[i] = a[i ^ lowbit(i)] + a[lowbit(i)];
        if (a[i] != m[1] and a[i] != m[2])
            for (int j = i; j; j ^= lowbit(j))
                f[i] = (f[i ^ lowbit(j)] + f[i]) % mod;
    }
    printf ("%d\n", f[final]);
}