PRM路径规划算法
路径规划作为机器人完成各种任务的基础,一直是研究的热点。研究人员提出了许多规划方法:如人工势场法、单元分解法、随机路标图(PRM)法、快速搜索树(RRT)法等。传统的人工势场、单元分解法需要对空间中的障碍物进行精确建模,当环境中的障碍物较为复杂时,将导致规划算法计算量较大。基于随机采样技术的PRM法可以有效解决高维空间和复杂约束中的路径规划问题。
PRM是一种基于图搜索的方法,它将连续空间转换成离散空间,再利用A*等搜索算法在路线图上寻找路径,以提高搜索效率。这种方法能用相对少的随机采样点来找到一个解,对多数问题而言,相对少的样本足以覆盖大部分可行的空间,并且找到路径的概率为1(随着采样数增加,P(找到一条路径)指数的趋向于1)。显然,当采样点太少,或者分布不合理时,PRM算法是不完备的,但是随着采用点的增加,也可以达到完备。所以PRM是概率完备且不最优的。

The PRM path planner constructs a roadmap in the free space of a given map using randomly sampled nodes in the free space and connecting them with each other. Once the roadmap has been constructed, you can query for a path from a given start location to a given end location on the map.
The probabilistic roadmap planner consists of two phases: a construction and a query phase. 学习阶段:在给定图的自由空间里随机撒点(自定义个数),构建一个路径网络图。查询阶段:查询从一个起点到一个终点的路径。
• Roadmap is a graph G(V, E) (无向网络图G,其中V代表随机点集,E代表所有可能的两点之间的路径集)
• Robot configuration q→Q_free is a vertex (每个点都要确保机器人与障碍物无碰撞)
• Edge (q1, q2) implies collision-free path between these robot configurations
• A metric is needed for d(q1,q2) (e.g. Euclidean distance) (Dist function计算Configuration Space中点与点之间的距离,判断是否是同一个点)
• Uses coarse sampling of the nodes, and fine sampling of the edges
• Result: a roadmap in Q_free
Step 1, Learning the Map
• Initially empty Graph G
• A configuration q is randomly chosen
• If q →Q_free then added to G (collision detection needed here)
• Repeat until N vertices chosen
• For each q, select k closest neighbors,
• Local planner connects q to neighbor q’
• If connect successful (i.e. collision free local path), add edge (q, q’)

参考这里的MATLAB代码,输入一幅500×500的地图,根据Roadmap Construction Algorithm建立网络图,然后使用A*算法搜索出一条最短路径。
PRM.m文件如下,注意下面代码中并没有选取k个最近点进行连接(或是限定连接距离),而是连接了全部的节点。

%% PRM parameters
map=im2bw(imread('map1.bmp')); % input map read from a bmp file. for new maps write the file name here
source=[10 10]; % source position in Y, X format
goal=[490 490]; % goal position in Y, X format
k=50; % number of points in the PRM
display=true; % display processing of nodes
if ~feasiblePoint(source,map), error('source lies on an obstacle or outside map'); end
if ~feasiblePoint(goal,map), error('goal lies on an obstacle or outside map'); end
imshow(map);
rectangle('position',[1 1 size(map)-1],'edgecolor','k')
vertex=[source;goal]; % source and goal taken as additional vertices in the path planning to ease planning of the robot
if display, rectangle('Position',[vertex(1,2)-5,vertex(1,1)-5,10,10],'Curvature',[1,1],'FaceColor','r'); end % draw circle
if display, rectangle('Position',[vertex(2,2)-5,vertex(2,1)-5,10,10],'Curvature',[1,1],'FaceColor','r'); end
tic; % tic-toc: Functions for Elapsed Time
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Step 1, Constructs the Map %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% iteratively add vertices
while length(vertex)<k+2
x = double(int32(rand(1,2) .* size(map))); % using randomly sampled nodes(convert to pixel unit)
if feasiblePoint(x,map),
vertex=[vertex;x];
if display, rectangle('Position',[x(2)-5,x(1)-5,10,10],'Curvature',[1,1],'FaceColor','r'); end
end
end
if display
disp('click/press any key');
% blocks the caller's execution stream until the function detects that the user has pressed a mouse button or a key while the Figure window is active
waitforbuttonpress;
end
%% attempts to connect all pairs of randomly selected vertices
edges = cell(k+2,1); % edges to be stored as an adjacency list
for i=1:k+2
for j=i+1:k+2
if checkPath(vertex(i,:),vertex(j,:),map);
edges{i}=[edges{i};j];
edges{j}=[edges{j};i];
if display, line([vertex(i,2);vertex(j,2)],[vertex(i,1);vertex(j,1)]); end
end
end
end
if display
disp('click/press any key');
waitforbuttonpress;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Step 2, Finding a Path using A* %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% structure of a node is taken as: [index of node in vertex, historic cost, heuristic cost, total cost, parent index in closed list (-1 for source)]
Q=[1 0 heuristic(vertex(1,:),goal) 0+heuristic(vertex(1,:),goal) -1]; % the processing queue of A* algorihtm, open list
closed=[]; % the closed list taken as a list
pathFound=false;
while size(Q,1) > 0 % while open-list is not empty
[A, I] = min(Q,[],1);% find the minimum value of each column
current = Q(I(4),:); % select smallest total cost element to process
Q=[Q(1:I(4)-1,:);Q(I(4)+1:end,:)]; % delete element under processing
if current(1)==2 % index of node in vertex==2(goal)
pathFound=true;break;
end
for mv = 1:length(edges{current(1)}) % iterate through all edges from the node
newVertex=edges{current(1)}(mv); % move to neighbor node
if length(closed)==0 || length(find(closed(:,1)==newVertex))==0 % not in closed(Ignore the neighbor which is already evaluated)
historicCost = current(2) + historic(vertex(current(1),:),vertex(newVertex,:)); % The distance from start to a neighbor
heuristicCost = heuristic(vertex(newVertex,:),goal);
totalCost = historicCost + heuristicCost;
add = true; % not already in queue with better cost
if length(find(Q(:,1)==newVertex))>=1
I = find(Q(:,1)==newVertex);
if totalCost > Q(I,4), add=false; % not a better path
else Q=[Q(1:I-1,:);Q(I+1:end,:);];add=true;
end
end
if add
Q=[Q;newVertex historicCost heuristicCost totalCost size(closed,1)+1]; % add new nodes in queue
end
end
end
closed=[closed;current]; % update closed lists
end
if ~pathFound
error('no path found')
end
fprintf('processing time=%d \nPath Length=%d \n\n', toc, current(4));
path=[vertex(current(1),:)]; % retrieve path from parent information
prev = current(5);
while prev > 0
path = [vertex(closed(prev,1),:);path];
prev = closed(prev, 5);
end
imshow(map);
rectangle('position',[1 1 size(map)-1],'edgecolor','k')
line(path(:,2),path(:,1),'color','r');
其它M文件:

%% checkPath.m function feasible=checkPath(n,newPos,map) feasible = true; dir=atan2(newPos(1)-n(1),newPos(2)-n(2)); for r=0:0.5:sqrt(sum((n-newPos).^2)) posCheck = n + r.*[sin(dir) cos(dir)]; if ~(feasiblePoint(ceil(posCheck),map) && feasiblePoint(floor(posCheck),map) && ... feasiblePoint([ceil(posCheck(1)) floor(posCheck(2))],map) && feasiblePoint([floor(posCheck(1)) ceil(posCheck(2))],map)) feasible = false;break; end if ~feasiblePoint(newPos,map), feasible = false; end end end %% feasiblePoint.m function feasible=feasiblePoint(point,map) feasible=true; % check if collission-free spot and inside maps % 0: obstacle 1: free space if ~(point(1)>=1 && point(1)<=size(map,1) && point(2)>=1 && point(2)<=size(map,2) && map(point(1),point(2))==1) feasible=false; end end %% heuristic.m function h=heuristic(X,goal) h = sqrt(sum((X-goal).^2)); end %% historic.m function h=historic(a,b) h = sqrt(sum((a-b).^2)); end

MATLAB Robotics System Toolbox
MATLAB的robotics system toolbox中提供了PRM路径规划方法,可以很方便的创建一个probabilistic roadmap path planner来进行路径规划。使用时有下面几点需要注意:
- Tune the Number of Nodes(调整节点数目)
Increasing the number of nodes can increase the efficiency of the path by giving more feasible paths. However, the increased complexity increases computation time. To get good coverage of the map, you might need a large number of nodes. Due to the random placement of nodes, some areas of the map may not have enough nodes to connect to the rest of the map. In this example, you create a large and small number of nodes in a roadmap.
% Create an occupancy grid map = robotics.OccupancyGrid(simpleMap, 2); % Create a simple roadmap with 50 nodes. prmSimple = robotics.PRM(map, 50); show(prmSimple)

% Create a dense roadmap with 250 nodes. prmComplex = robotics.PRM(map,250); show(prmComplex)
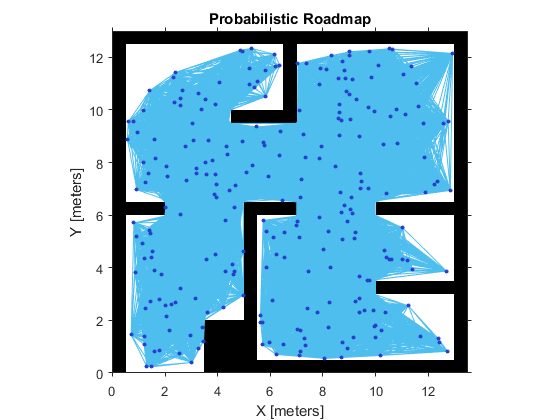
- Tune the Connection Distance(调整连接距离)
Use the ConnectionDistance property on the PRM object to tune the algorithm. ConnectionDistance is an upper threshold for points that are connected in the roadmap. Each node is connected to all nodes within this connection distance that do not have obstacles between them. By lowering the connection distance, you can limit the number of connections to reduce the computation time and simplify the map. However, a lowered distance limits the number of available paths from which to find a complete obstacle-free path. When working with simple maps, you can use a higher connection distance with a small number of nodes to increase efficiency. For complex maps with lots of obstacles, a higher number of nodes with a lowered connection distance increases the chance of finding a solution.
% Save the random number generation settings using the rng function. The saved settings enable you to reproduce the same points and see the effect of changingConnectionDistance.
rngState = rng;
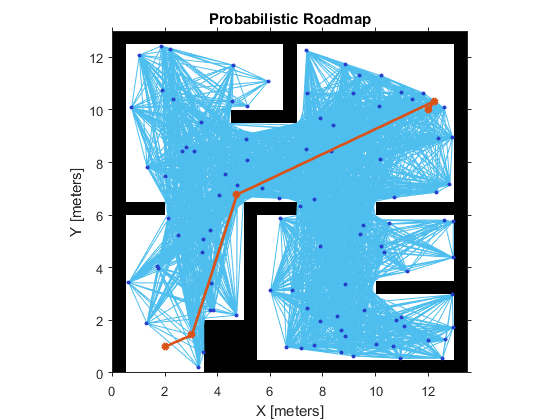
% Create a roadmap with 100 nodes and calculate the path. The default ConnectionDistance is set to inf. prm = robotics.PRM(map, 100);
startLocation = [2 1]; endLocation = [12 10]; path = findpath(prm,startLocation,endLocation);
show(prm)
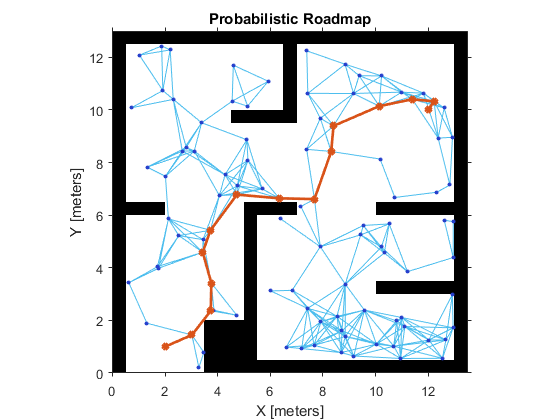
% Reload the random number generation settings to have PRM use the same nodes rng(rngState);
% Lower ConnectionDistance to 2 m prm.ConnectionDistance = 2; path = findpath(prm, startLocation, endLocation); show(prm)
-
Create or Update PRM
This roadmap changes only if you call update or change the properties in the PRM object. When properties change, any method (update, findpath, or show) called on the object triggers the roadmap points and connections to be recalculated. Because recalculating the map can be computationally intensive, you can reuse the same roadmap by calling findpath with different starting and ending locations. 即当使用update函数进行更新或者改变PRM对象属性后,调用findpath、show等方法会引发重新计算。
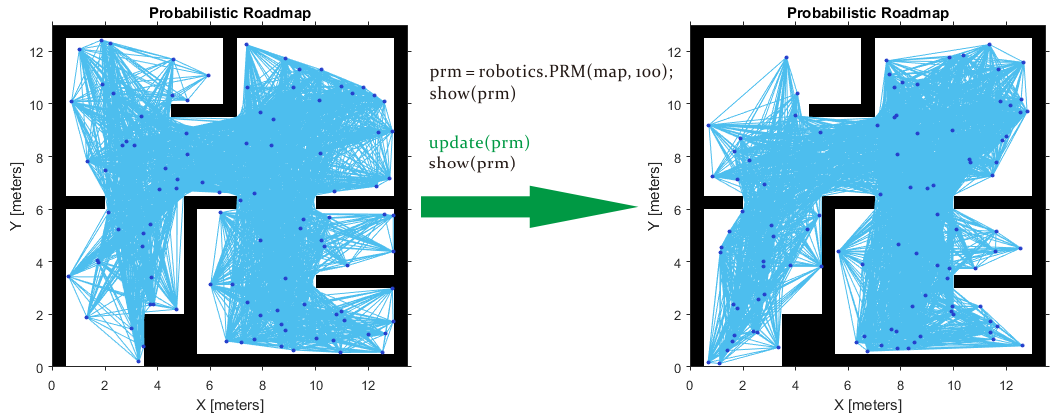
The PRM algorithm recalculates the node placement and generates a new network of nodes
- Inflate the Map Based on Robot Dimension
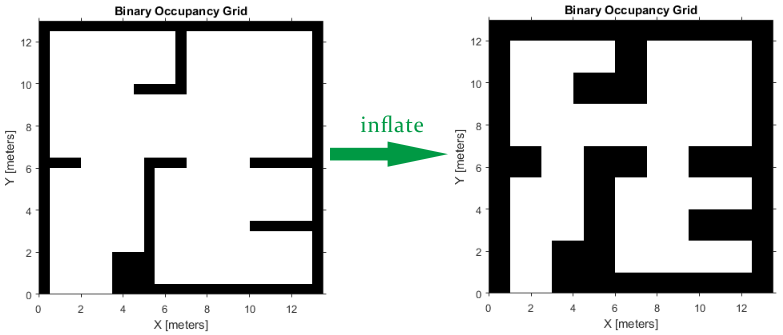
PRM does not take into account the robot dimension while computing an obstacle free path on a map. Hence, you should inflate the map by the dimension of the robot, in order to allow computation of an obstacle free path that accounts for the robot's size and ensures collision avoidance for the actual robot. This inflation is used to add a factor of safety on obstacles and create buffer zones between the robot and obstacle in the environment. The inflate method of an occupancy grid object converts the specified radius to the number of cells rounded up from the resolution*radius value.
robotRadius = 0.2; mapInflated = copy(map); inflate(mapInflated,robotRadius); show(mapInflated)
- Find a Feasible Path on the Constructed PRM
Since you are planning a path on a large and complicated map, larger number of nodes may be required. However, often it is not clear how many nodes will be sufficient. Tune the number of nodes to make sure there is a feasible path between the start and end location.
path = findpath(prm, startLocation, endLocation)
while isempty(path) % No feasible path found yet, increase the number of nodes prm.NumNodes = prm.NumNodes + 10; % Use the |update| function to re-create the PRM roadmap with the changed attribute update(prm); % Search for a feasible path with the updated PRM path = findpath(prm, startLocation, endLocation); end
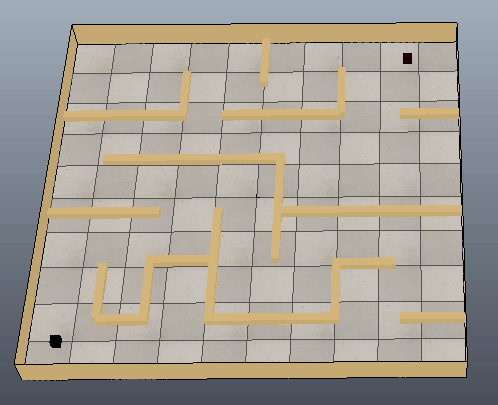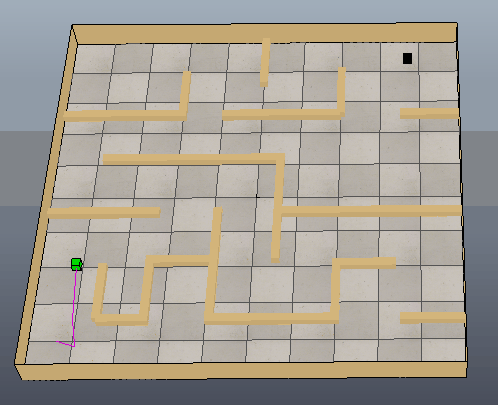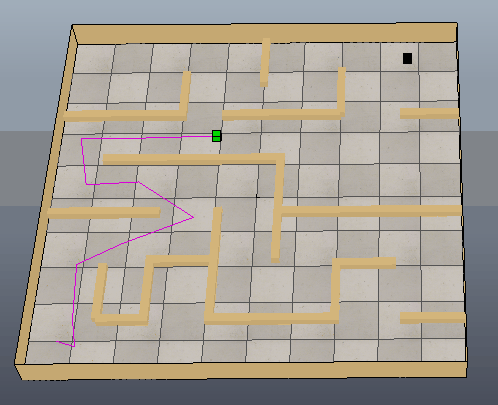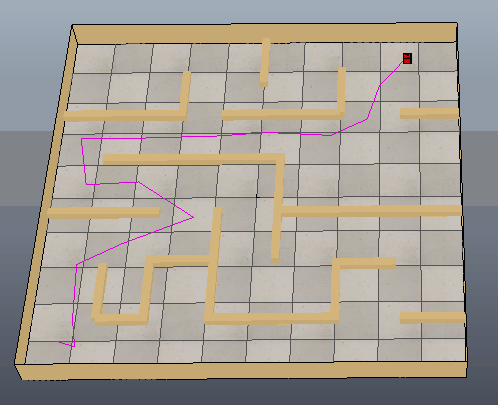
下面在VREP仿真软件中搭建一个简单的场景(修改practicalPathPlanningDemo.ttt):在地图正上方放置一个视觉传感器采集地图黑白图像,绿色方块代表起始位置,红色方块代表目标位置。然后使用MATLAB中的PRM进行路径规划。
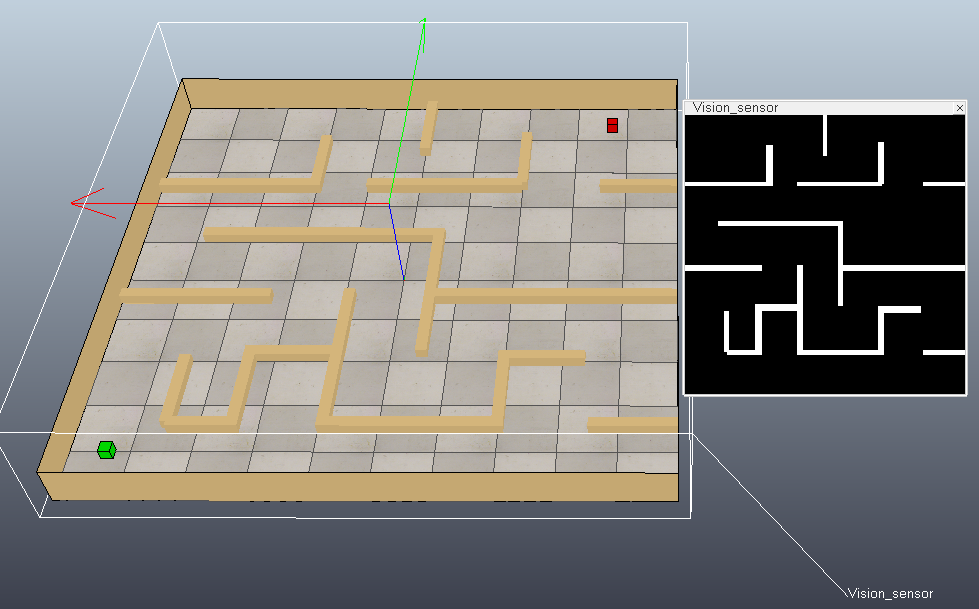
MATLAB代码如下:
function simpleTest()
disp('Program started');
vrep=remApi('remoteApi'); % using the prototype file (remoteApiProto.m)
vrep.simxFinish(-1); % just in case, close all opened connections
clientID=vrep.simxStart('127.0.0.1',19999,true,true,5000,5);
if (clientID>-1)
disp('Connected to remote API server');
[returnCode,sensorHandle] = vrep.simxGetObjectHandle(clientID,'Vision_sensor',vrep.simx_opmode_blocking);
[returnCode,objectHandle] = vrep.simxGetObjectHandle(clientID,'start',vrep.simx_opmode_blocking);
[returnCode,goalHandle] = vrep.simxGetObjectHandle(clientID,'goal',vrep.simx_opmode_blocking);
% Retrieves the image of a vision sensor as an image array(each image pixel is a byte (greyscale image))
[returnCode,resolution,image] = vrep.simxGetVisionSensorImage2(clientID, sensorHandle, 1, vrep.simx_opmode_blocking);
% Creates a BinaryOccupancyGrid object with resolution specified in cells per meter.
width = 5; height = 5; % Map width / height, specified as a double in meters.
grid = robotics.BinaryOccupancyGrid(image, resolution(1) / width);
grid.GridLocationInWorld = [-width/2, -height/2]; % world coordinates of the bottom-left corner of the grid
% Inflate the Map Based on Robot Dimension
inflate(grid, 0.1);
% Create a roadmap with 200 nodes and calculate the path
prm = robotics.PRM(grid, 200);
prm.ConnectionDistance = 1;
[returnCode,startLocation] = vrep.simxGetObjectPosition(clientID,objectHandle,-1,vrep.simx_opmode_blocking);
[returnCode,endLocation] = vrep.simxGetObjectPosition(clientID,goalHandle, -1,vrep.simx_opmode_blocking);
path = findpath(prm, double(startLocation(1:2)), double(endLocation(1:2)));
show(prm)
% Simply jump through the path points, no interpolation here:
for i=1 : size(path,1)
pos = [path(i,:), 0.05];
vrep.simxSetObjectPosition(clientID, objectHandle, -1, pos, vrep.simx_opmode_blocking);
pause(0.5);
end
% Now close the connection to V-REP:
vrep.simxFinish(clientID);
else
disp('Failed connecting to remote API server');
end
vrep.delete(); % call the destructor!
disp('Program ended');
end
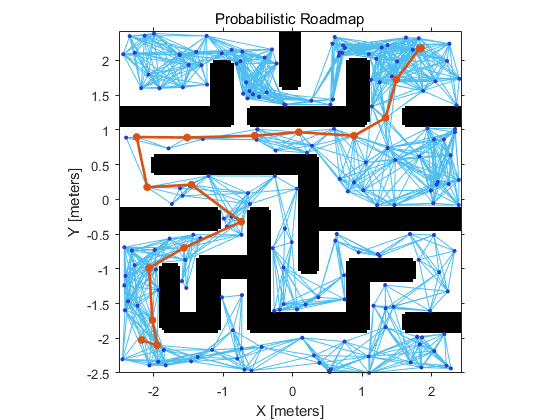
下图是MATLAB根据获取到的黑白图像创建的栅格图,并进行路径规划的结果:
下图可以看出方块沿着生成的路径移动到目标位置,只是路径还需要进一步优化。
参考:
Path Planning in Environments of Different Complexity
Code for Robot Path Planning using Probabilistic Roadmap
Roadmap Methods for Multiple Queries
Probabilistic Roadmap Path Planning




 浙公网安备 33010602011771号
浙公网安备 33010602011771号