利用奇异值分解（SVD）简化数据

• 特征值与特征向量

　　下面这部分内容摘自：强大的矩阵奇异值分解(SVD)及其应用

    特征值分解和奇异值分解在机器学习领域都是属于满地可见的方法。两者有着很紧密的关系，在接下来会谈到，特征值分解和奇异值分解的目的都是一样，就是提取出一个矩阵最重要的特征。先谈谈特征值分解吧：

    如果说一个向量v是方阵A的特征向量，则可以表示成下面的形式：

    这时候λ就被称为特征向量v对应的特征值，一个矩阵的一组特征向量是一组正交向量。特征值分解是将一个矩阵分解成下面的形式：

    其中Q是这个矩阵A的特征向量组成的矩阵，Σ是一个对角阵，每一个对角线上的元素就是一个特征值。首先要明确的是，一个矩阵其实就对应一个线性变换，因为一个矩阵乘以一个向量，其实就相当于对这个向量进行了线性变换。比如说下面的一个矩阵：

　　它其实对应的线性变换是下面的形式：

　　因为这个矩阵M乘以一个向量(x,y)^T的结果是：

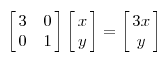    上面的矩阵是对称的，所以这个变换是一个对x，y轴的拉伸变换（每一个对角线上的元素将会对一个维度进行拉伸变换，当值>1时，是拉长，当值<1时时缩短），当矩阵不是对称的时候，假如说矩阵是下面的样子：

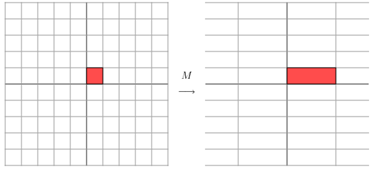
　　它所描述的变换是下面的样子：

　　这其实是在平面上对一个轴进行的拉伸变换（如蓝色的箭头所示），在图中，蓝色的箭头是一个最主要的变化方向（变化方向可能有不止一个），如果我们想要描述好一个变换，那我们就描述好这个变换主要的变化方向就好了。反过头来看看之前特征值分解的式子，分解得到的Σ矩阵是一个对角阵，里面的特征值是由大到小排列的，这些特征值所对应的特征向量就是描述这个矩阵变化方向（从主要的变化到次要的变化排列）。

　　当矩阵是高维的情况下，那么这个矩阵就是高维空间下的一个线性变换，这个线性变化可能没法通过图形来表示，但是可以想象，这个变换也同样有很多的变换方向，我们通过特征值分解得到的前N个特征向量，那么就对应了这个矩阵最主要的N个变化方向。我们利用这前N个变化方向，就可以近似这个矩阵（变换）。也就是之前说的：提取这个矩阵最重要的特征。总结一下，特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征是什么，可以将每一个特征向量理解为一个线性的子空间，我们可以利用这些线性的子空间干很多的事情。不过，特征值分解也有很多的局限，比如说变换的矩阵必须是方阵。

　　特征值分解是一个提取矩阵特征很不错的方法，但是它只是对方阵而言的，在现实的世界中，我们看到的大部分矩阵都不是方阵，比如说有N个学生，每个学生有M科成绩，这样形成的一个N * M的矩阵就不可能是方阵，我们怎样才能描述这样普通的矩阵呢的重要特征呢？奇异值分解可以用来干这个事情。

• 奇异值分解

　　奇异值分解（SVD）不仅是矩阵理论和矩阵计算的最基本、最重要的工具之一，而且在最优化问题，控制理论，系统辨识和信号处理等许多领域都有直接应用。为了引入矩阵奇异值的概念，先介绍几个引理。

引理1. 设A∈C^m×n,则 rank(A^HA)=rank(AA^H)=rank(A)。

引理2. 设A∈C^m×n,则A^HA与AA^H的特征值均为非负实数；且其非零特征值相同，并且非零特征值的个数等于rank(A)

定义： 设A∈C_r^m×n(r>0), A^HA的特征值为λ₁≥λ₂≥...≥λ_r>λ_r+1=...=λ_n=0，则称σ_i为A的奇异值

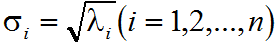
定理：设A∈C_r^m×n(r>0),则存在m阶酉矩阵U和n阶酉矩阵V，使得

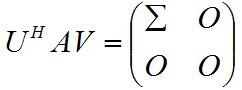
　　其中Σ=diag(σ₁,σ₂,...,σ_i)，而σ_i为A的非零奇异值，将上式改写为

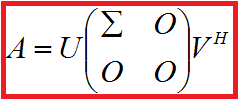
　　则称之为矩阵A的奇异值分解。

　　其中，U的每一列称作左奇异向量；Σ是对角矩阵；V的每一列（即V的共轭转置矩阵V^H的每一行）称作右奇异向量；对角线上的值按照从大到小排列，称作奇异值。U的列向量是AA^H的单位正交特征向量，V的列向量是A^HA的单位正交特征向量，Σ矩阵对角线上的值实际就是AA^H或者A^HA特征值的平方根。计算SVD实际上就是计算A^HA或者AA^H的特征值和特征向量，然后将它们组合成上面表达式的形式（注意所得结果需要进行检验——参考矩阵论简明教程P121）。

　　例：对矩阵A进行奇异值分解

$$A=\left(\begin{array}{c}0 \\-1 \\0 \\1\end{array}\begin{array}{c}1 \\0 \\2 \\0\end{array}\right)$$

　　解：因为

$$A^HA=\left(\begin{array}{cc}2 & 0 \\0 & 5\end{array}\right)$$

则A的非零奇异值为$\sqrt{2}$，$\sqrt{5}$，A^HA对应特征值5和2的标准正交特征向量为$u_1=\left(\begin{array}{c}0 \\1\end{array}\right)$，$u_2=\left(\begin{array}{c}1 \\0\end{array}\right)$，而AA^H对应特征值5和2的标准正交特征向量为：$v_1=\left(\begin{array}{c}\frac{1}{\sqrt{5}} \\0 \\\frac{2}{\sqrt{5}} \\0\end{array}\right)$，$v_2=\left(\begin{array}{c}0 \\\frac{-1}{\sqrt{2}} \\0 \\\frac{1}{\sqrt{2}}\end{array}\right)$，AA^H对应特征值0的标准正交特征向量为：$v_3=\left(\begin{array}{c}\frac{-2}{\sqrt{5}} \\0 \\\frac{1}{\sqrt{5}} \\0\end{array}\right)$，$v_4=\left(\begin{array}{c}0 \\\frac{1}{\sqrt{2}} \\0 \\\frac{1}{\sqrt{2}}\end{array}\right)$. 因此矩阵A的奇异值分解为：

• 使用numpy进行矩阵奇异值分解

 　　Numpy中linalg线性代数模块含有SVD函数，可以方便的进行奇异值分解。以矩阵[[1,1],[1,7]]为例使用numpy中的函数进行分解：

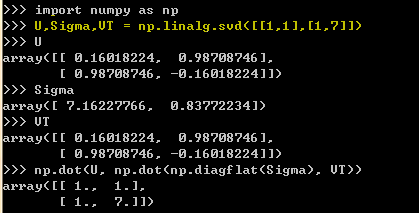
　　注意Sigma矩阵以一维行向量的形式返回（Sigma矩阵中除了对角元素其它均为0），这种仅返回对角元素的方式能够节省空间。

　　再以如下矩阵为例进行SVD分解

　　计算结果为:
　　>>>Sigma
　　array([ 9.72140007e+00, 　　5.29397912e+00, 　　6.84226362e-01,　　7.16251492e-16,　　4.85169600e-32])

　　前三个奇异值比其他的值大很多，于是可以将最后两个值去掉（在很多情况下，数据中的一小段携带了数据集中的大部分信息，其他的信息要么是噪声，要么就是毫不相关的信息。一般在某个奇异值的数目（r个）之后，其它奇异值都为0，这就意味着数据集中仅有r个重要特征，而其它特征都是噪声或冗余特征）。接下来，原始数据集就可以用如下结果来近似：

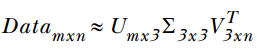
        中间矩阵∑为对角阵，对角元素值为Data矩阵的奇异值，且已经从大到小排序，即使去掉特征值小的那些特征，依然可以很好地重构出原始矩阵。如下图：其中阴影部分代表去掉小奇异值，近似重构时的三个矩阵。这三个矩阵的面积之和（从存储观点来说，矩阵面积越小，存储量就越小）要远远小于原始的矩阵，我们如果想要压缩空间来表示原矩阵，则存储U、Σ、V就好了。

　　接下来我们验证一下近似的效果。首先构建一个3×3的对角矩阵Sig3：>>>Sig3=np.diagflat([Sigma[0], Sigma[1], Sigma[2]])

　　取矩阵U的前3列和矩阵VT的前3行进行计算： >>>np.dot(U[:,:3],  np.dot(Sig3 ,VT[:3,:]))    

　　结果如下图所示，可以看出用近似矩阵成功的重构出被分解的矩阵，即通过三个矩阵对原始矩阵进行了近似。

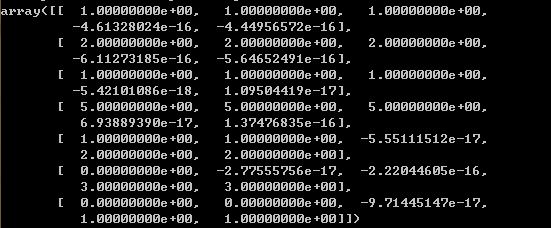
　　那么如何确定要保留前几个奇异值呢？确定要保留的奇异值的数目有很多种策略，其中一个典型的做法就是保留矩阵中90%的能量信息。为了计算总能量信息，将所有的奇异值求平方和。于是可以将奇异值的平方和累加到总值的90%为止。另一个策略就是，当矩阵上有上万的奇异值时,那么就保留前面的2000或3000个。尽管后一种方法不太优雅，但是在实际中更容易实施。之所以说它不够优雅，就是因为在任何数据集上都不能保证前3000个奇异值就能够包含90%的能量信息。但在通常情况下，使用者往往都对数据有足够的了解，从而就能够做出类似的假设了。

•  基于协同过滤的推荐引擎

　　推荐引擎利用基于内容、基于用户行为、基于社交关系网络等多种方法，为用户推荐其喜欢的商品或内容。协同过滤是通过将用户和其他用户的数据进行对比来实现推荐的。
　　当知道了两个用户或两个物品之间的相似度，我们就可以利用已有的数据来预测未知的用户喜好。例如，我们试图对某个用户喜欢的电影进行预测。推荐引擎发现有一部电影该用户还没看过。然后，它就会计算该电影和用户看过的电影之间的相似度，如果其相似度很高，推荐算法就会认为用户喜欢这部电影。假如我们要为食品销售网站做一个推荐系统，则可以根据食品的配料、热量、烹调类型等特征进行相似度的计算。如果该网站改为销售电子产品，则描述电子产品的属性和描述食品的属性又有所不同。我们不利用专家所给出的重要特征来描述物品从而计算它们之间的相似度，而是利用用户对它们的意见来计算相似度。这就是协同过滤中所使用的方法。它并不关心物品的描述属性，而是严格地按照不同用户的观点来计算相似度。
　　下图给出了由一些用户对部分菜肴的评级信息所组成的矩阵。用户可以采用1 到5 之间的任意一个整数来对菜评级，如果没有尝过某道菜，则评级为0

　　我们计算一下手撕猪肉和烤牛肉之间的相似度。首先使用欧氏距离来计算，手撕猪肉和烤牛肉的欧氏距离为：

　　而手撕猪肉和鳗鱼饭之间的欧氏距离为：

　　

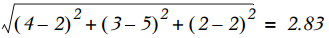
　　由于手撕猪肉和烤牛肉的距离小于手撕猪肉和鳗鱼饭的距离， 因此手撕猪肉与烤牛肉比与鳗鱼饭更为相似。另一个常用的距离计算方法就是余弦相似度（cosine similarity)，其计算的是两个向量夹角的余弦值。如果夹角为90度，则相似度为0；如果两个向量的方向相同，则相似度为1。两个向量A和B的余弦相似度的定义如下：

　　余弦距离使用两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比欧氏距离，余弦距离更加注重两个向量在方向上的差异。从下图可以看出，欧氏距离衡量的是空间各点的绝对距离，跟各个点所在的位置坐标直接相关；而余弦距离衡量的是空间向量的夹角，更加体现在方向上的差异，而不是位置。如果保持A点位置不变，B点朝原方向远离坐标轴原点，那么这个时候余弦距离是保持不变的（因为夹角没有发生变化），而A、B两点的欧氏距离显然在发生改变，这就是欧氏距离和余弦距离之间的不同之处。

　　欧氏距离和余弦距离各自有不同的计算方式和衡量特征，因此它们适用于不同的数据分析模型：欧氏距离能够体现个体数值特征的绝对差异，所以更多的用于需要从维度的数值大小中体现差异的分析，如使用用户行为指标分析用户价值的相似度或差异。余弦距离更多的是从方向上区分差异，而对绝对的数值不敏感，更多的用于使用用户对内容评分来区分兴趣的相似度和差异，同时修正了用户间可能存在的度量标准不统一的问题（因为余弦距离对绝对数值不敏感）。

　　计算相似度时可以采用基于物品（item-based）的相似度或基于用户（user-based）的相似度。矩阵行与行之间比较的是基于用户的相似度，列与列之间比较的是基于物品的相似度。到底使用哪一种相似度，取决于用户或物品的数目。如果用户数目很多，那么我们可能倾向于使用基于物品相似度的计算方法。对于大部分推荐引擎而言，用户数量往往大于商品的数量。

　　推荐未尝过的菜肴:
　　推荐系统的工作过程是给定一个用户，系统会为此用户返回N个最好的推荐菜。为了实现这一点，需要我们做到：
（1）寻找用户没有评级的菜肴，即在用户—物品矩阵中的0值 
（2）在用户没有评级的所有物品中，对每个物品预计一个可能的评级分数
（3）对这些物品的评分从高到低进行排序，返回前N个物品

 　　假定真实的评价矩阵如下表所示，其中很多物品都没有评分。

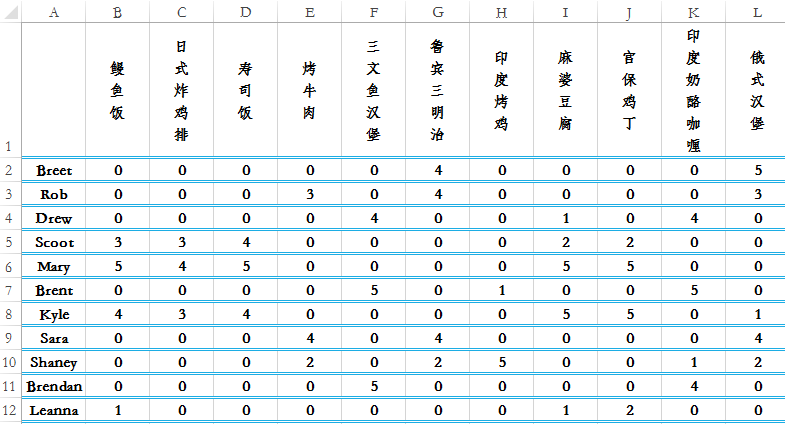
　　下面我们对该矩阵进行SVD分解，了解其需要多少维特征。首先对奇异值求平方和，然后计算总能量的90%：

　　U, sigma, VT = np.linalg.svd(mat)
　　Sig2 = sigma**2
　　sum(Sig2)*0.9

　　结果为487.8，然后计算前几个元素累加所包含的能量达到90%，当计算到前4个元素时（sum(Sig2[:,3]=500.5>487.8），就可以了。用户的评分数据是稀疏矩阵，可以用SVD将数据映射到低维空间，然后计算低维空间中的item之间的相似度，对用户未评分的item进行评分预测，最后将预测评分高的item推荐给用户。

　　下面代码将给第1号用户Rob推荐3个估计评分最高的食物：

# -*- coding: utf-8 -*-
import numpy as np

# 计算欧氏距离相似度(距离为0时相似度为1,距离非常大时相似度趋于0)
def ecludSim(inA, inB):
    return 1.0 / (1.0 + np.linalg.norm(inA - inB))


# 计算余弦相似度
def cosSim(inA, inB):
    num = np.inner(inA, inB)
    denom = np.linalg.norm(inA) * np.linalg.norm(inB)
    return 0.5 + 0.5 * (num / denom) # 归一化到0到1之间


# 计算在给定相似度计算方法的条件下,用户对物品的估计评分值
# 参数dataMat表示数据矩阵,user表示用户编号,simMeas表示相似度计算方法,item表示物品编号
def standEst(dataMat, user, simMeas, item):
    n = dataMat.shape[1] # 获取物品数目
    U, Sigma, VT = np.linalg.svd(dataMat)       # 进行奇异值分解
    transform = np.dot(U[:,:4].T, dataMat)      # 对行进行压缩
    
    simTotal = 0.0; ratSimTotal = 0.0
    for j in range(n):                  # 遍历每个物品
        userRating = dataMat[user,j]    # 用户对第j个用品的评分
        if userRating == 0:
            continue
        similarity = simMeas(transform[:,item], transform[:,j] ) # 比较item列与第j列物品的相似度
        print 'the %d and %d similarity is: %f' % (item, j, similarity)
        simTotal += similarity
        ratSimTotal += similarity * userRating

    if simTotal == 0: 
        return 0
    else: 
        print "item %d rating: %f" % (item, ratSimTotal/simTotal )
        return ratSimTotal/simTotal  # 用户评分归一化到0-5
        


# 产生最高的N个推荐结果,不过不指定N,默认值为3
def recommend(dataMat, user, N=3, simMeas=cosSim):
    unratedItems = np.nonzero(dataMat[user,:] == 0)[0]  # 寻找未评级的物品
    if len(unratedItems) == 0:         # 如果不存在未评分物品,则退出函数
        return 'you rated everything'
    itemScores = []
    for item in unratedItems:        # 对所有未评分物品进行预测得分
        estimatedScore = standEst(dataMat, user, simMeas, item)
        itemScores.append((item, estimatedScore))
    # 对itemScores进行从大到小排序，返回前N个未评分物品
    return sorted(itemScores, key=lambda jj: jj[1], reverse=True)[:N] 


if __name__ == "__main__":
    mat=np.array([[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 5],\
                [0, 0, 0, 3, 0, 4, 0, 0, 0, 0, 3],\
                [0, 0, 0, 0, 4, 0, 0, 1, 0, 4, 0],\
                [3, 3, 4, 0, 0, 0, 0, 2, 2, 0, 0],\
                [5, 4, 5, 0, 0, 0, 0, 5, 5, 0, 0],\
                [0, 0, 0, 0, 5, 0, 1, 0, 0, 5, 0],\
                [4, 3, 4, 0, 0, 0, 0, 5, 5, 0, 1],\
                [0, 0, 0, 4, 0, 4, 0, 0, 0, 0, 4],\
                [0, 0, 0, 2, 0, 2, 5, 0, 0, 1, 2],\
                [0, 0, 0, 0, 5, 0, 0, 0, 0, 4, 0],\
                [1, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0]])
         
    ret = recommend(mat, 1, N=3, simMeas=cosSim)
    print ret

　　输出结果如下所示：

the 0 and 3 similarity is: 0.498297
the 0 and 5 similarity is: 0.498702
the 0 and 10 similarity is: 0.540399
item 0 rating: 3.324381
the 1 and 3 similarity is: 0.497432
the 1 and 5 similarity is: 0.497414
the 1 and 10 similarity is: 0.539074
item 1 rating: 3.324277
the 2 and 3 similarity is: 0.497835
the 2 and 5 similarity is: 0.497894
the 2 and 10 similarity is: 0.539558
item 2 rating: 3.324300
the 4 and 3 similarity is: 0.495847
the 4 and 5 similarity is: 0.500120
the 4 and 10 similarity is: 0.501394
item 4 rating: 3.334001
the 6 and 3 similarity is: 0.750797
the 6 and 5 similarity is: 0.636231
the 6 and 10 similarity is: 0.623186
item 6 rating: 3.316499
the 7 and 3 similarity is: 0.500010
the 7 and 5 similarity is: 0.502570
the 7 and 10 similarity is: 0.544420
item 7 rating: 3.324867
the 8 and 3 similarity is: 0.500932
the 8 and 5 similarity is: 0.502238
the 8 and 10 similarity is: 0.544006
item 8 rating: 3.324616
the 9 and 3 similarity is: 0.530070
the 9 and 5 similarity is: 0.518088
the 9 and 10 similarity is: 0.517555
item 9 rating: 3.330896
[(4, 3.3340010557993547), (9, 3.3308956173494804), (7, 3.3248674803258673)]

　　代码中最关键的地方（标黄色背景的两行）在于如何利用SVD将高维数据映射成低维数据。

　　假设矩阵A的每一行表示一个样本，每一列表示一个特征，将一个m*n的矩阵变换成一个m*r的矩阵，这样就会使得本来有n个feature的矩阵，变成了有r个feature了（r < n)，这其实就是对矩阵信息的一种提炼。用数学语言表示就是：

　　根据之前提过的使用奇异值分解来近似A矩阵：

　　在上式两边同时乘上一个矩阵V，由于V是一个正交的矩阵，所以V转置乘以V得到单位阵I，所以可以化成下面的式子：$$A_{m\times n}V_{n\times r}\approx U_{m\times r}\Sigma _{r\times r}V^T{}_{r\times n}V_{n\times r}=U_{m\times r}\Sigma _{r\times r}=\tilde{A}_{m\times r}$$

　　这里是将一个m*n的矩阵压缩成一个m*r的矩阵，也就是对列进行压缩，如果我们想对行进行压缩（可以理解为，将一些相似的sample合并在一起，或者将一些没有太大价值的sample去掉）怎么办呢？同样我们写出一个通用的行压缩例子：

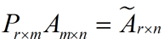
 　　这样就从一个m行的矩阵压缩到一个r行的矩阵了，对SVD来说也是一样的，我们对SVD分解的式子两边乘以U的转置U^T，这样我们就得到了对行进行压缩的式子：$$U_{m\times r}^TA_{m\times n}\approx U_{m\times r}^TU_{m\times r}\Sigma _{r\times r}V_{r\times n}^T=\Sigma _{r\times r}V_{r\times n}^T=\tilde{A}_{r\times n}$$

　　如此则将m行数据压缩成r行数据，其含义就是去除那些十分相近的数据。

•  基于SVD的图像压缩

　　下面将对一张手写的数字图像进行压缩。原始的图像大小是32×32=1024像素 ，我们能否使用更少的像素来表示这张图呢？如果能对图像进行压缩，那么就可以节省空间或带宽开销了。我们可以使用SVD来对数据降维，从而实现图像的压缩。

00000000000000110000000000000000
00000000000011111100000000000000
00000000000111111110000000000000
00000000001111111111000000000000
00000000111111111111100000000000
00000001111111111111110000000000
00000000111111111111111000000000
00000000111111100001111100000000
00000001111111000001111100000000
00000011111100000000111100000000
00000011111100000000111110000000
00000011111100000000011110000000
00000011111100000000011110000000
00000001111110000000001111000000
00000011111110000000001111000000
00000011111100000000001111000000
00000001111100000000001111000000
00000011111100000000001111000000
00000001111100000000001111000000
00000001111100000000011111000000
00000000111110000000001111100000
00000000111110000000001111100000
00000000111110000000001111100000
00000000111110000000011111000000
00000000111110000000111111000000
00000000111111000001111110000000
00000000011111111111111110000000
00000000001111111111111110000000
00000000001111111111111110000000
00000000000111111111111000000000
00000000000011111111110000000000
00000000000000111111000000000000

# -*- coding: cp936 -*-
import numpy as np
from matplotlib import pyplot as plt

def printMat(inMat, thresh=0.8):
    for i in range(32):
        for k in range(32):
            if float(inMat[i,k]) > thresh:
                print 1,
            else: print 0,
        print ''

def imgCompress(numSV=3, thresh=0.8):
    myl = []
    for line in open('data.txt').readlines():
        newRow = []
        for i in range(32):
            newRow.append(int(line[i]))
        myl.append(newRow)
    myMat = np.mat(myl)
    #print "****original matrix******"
    #printMat(myMat, thresh)
    U,Sigma,VT = np.linalg.svd(myMat)
    SigRecon = np.mat(np.zeros((numSV, numSV)))
    for k in range(numSV):    #construct diagonal matrix from vector
        SigRecon[k,k] = Sigma[k]
    reconMat = U[:,:numSV]*SigRecon*VT[:numSV,:]
    #print "****reconstructed matrix using %d singular values******" % numSV
    #printMat(reconMat, thresh)
    return (myMat, reconMat)


if __name__ == "__main__":

    img1, img2 = imgCompress()

    plt.subplot(121),plt.imshow(img1,cmap ='gray'),plt.title('Original')
    plt.subplot(122),plt.imshow(img2,cmap ='gray'),plt.title('Reconstruction')
    
    plt.show()

　　结果如下图所示，左边为原始矩阵图像，右边为重建矩阵的灰度图。

 　　可以看到，只需要3个奇异值就能相当精确地对图像实现重构。U和V^T都是32×3的矩阵，因此这些矩阵中包含的元素为32×3+32×3+3=195。和原来的1024相比获得了5倍的压缩比。

 　　下面用一幅普通的图片来进行一下测试。用OpenCV以灰度图模式读入，然后分别选用100,50,20,10,5这五个奇异值进行压缩并重建。

# -*- coding: cp936 -*-
import numpy as np
import cv2
from matplotlib import pyplot as plt


def imgCompress(img, numSV=3):

    U, Sigma, VT = np.linalg.svd(img)
    SigRecon = np.asmatrix(np.diag(Sigma[:numSV]))
    reconMat = U[:,:numSV] * SigRecon * VT[:numSV,:]
    
    return reconMat


if __name__ == "__main__":
    
    myMat = cv2.imread('data.jpg',0) # Loads image in grayscale mode
    numSV = [100, 50, 20, 10, 5]
    img = []
    for i in range(5):
        img.append(imgCompress(myMat, numSV=numSV[i]))
    
    plt.subplot(231),plt.imshow(myMat, cmap='gray'),plt.title('Original')
    for i in range(5):
        plt.subplot(232+i),plt.imshow(img[i], cmap='gray'),plt.title('numSV='+str(numSV[i]))
    
    plt.show()

　　效果如下图，可以看出压缩到10个奇异值的时候，图片特征还算明显，可以看出这是homer simpson...

　　处理彩色图片上要复杂一点，因为有RGB三个通道的数据，对应的矩阵形状是3维的。要用OpenCV中的split和merge函数分离三个通道数据最后再合并处理，我尝试了几次没有成功就懒得再试了...
　　有一点需要注意：cv2.imread()读入彩色图像时，返回的ndarray是按照B,G,R的顺序排列的，而matplotlib中的plt.imshow()显示彩色图像时，是按照RGB的顺序显示的。可以用cv2.cvtColor(image , cv2.COLOR_BGR2RGB)进行转换。

•  总结

　　SVD是一种强大的降维工具，我们可以利用SVD来逼近矩阵并从中提取重要特征。

 

参考：

Machine Learning in Action  chapter 14 Simplifying data with the singular value decomposition

《矩阵论》 戴华，科学出版社

《矩阵论简明教程》 徐仲，科学出版社

《数学之美》 吴军，第15章 矩阵运算和文本处理中的两个分类问题

SVD分解算法及其应用

强大的矩阵奇异值分解(SVD)及其应用

谈谈SVD和LSA