「奶龙」题解

T660627 「奶龙」新闻

有一个显而易见的分层结构，设树上深度 \(\le x\) 的节点数 \(s_x=i\)，则有：

\[\displaystyle \left \{\begin{array}{l} ki \le s_{x + 1} < k(i + 1),\ i < \lfloor \dfrac{n}{k} \rfloor,\\ \max(k\lfloor \dfrac{n}{k} \rfloor,i) \le s_{x + 1} \le n,\ i \ge \lfloor \dfrac{n}{k} \rfloor. \end{array}\right. \]

然后显然一个区间是否合法只和它自己有关，所以有一个显而易见的 DP：跑出来所有有效的区间，有 \([i,j]\) 到 \([j+1,k]\) 的转移系数是 \(\binom{n-j}{k-j}(j-i+1)^{k-j}\)。暴力枚举 \(i,j,k\) 就有一个根据实现是否精细决定的 \(O(n^3)\) 或者 \(O(n^3 \log n)\) 的做法，至此有 30pts。

然后我们发现 \(k\) 给的很小，所以考虑分析一下有效区间的状态。事实上大概会形如下面的图片。

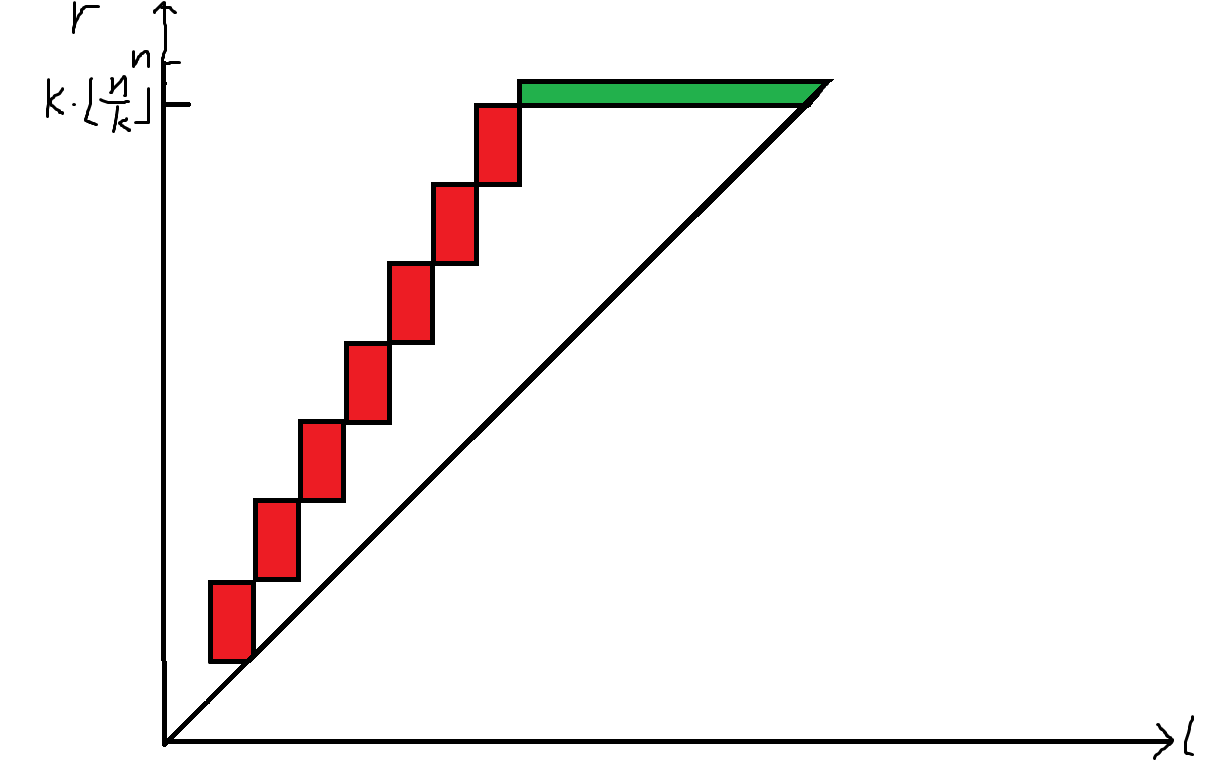
所以合法的转移显然只有 \(O(nk+(n \bmod k)^3)\)，同样根据实现是否精细有可能带一个 \(\log\)。注意到 \(n \bmod k\) 被我卡满到 \(O(k)\) 了，所以随便写一下有 60pts。

容易发现转移 \(O(k^3)\) 的部分完全来自于绿色部分。所以只要不在 \(k \lfloor \dfrac{n}{k} \rfloor \sim n\) 的区间里反复转移就能做到 \(O(nk)\)。注意到这部分节点可以随便挂，所以只要能求出来下面问题的答案即可：

有 \(m\) 个根，有 \(n\) 个节点往这 \(m\) 个根下面挂，所形成的森林数量。我们创建 \(m+1\) 个节点，节点 \(0\) 为根，节点 \(0\) 的儿子为节点 \(1 \sim m\)，之后我们本来的 \(n\) 个节点编号就变为了 \(m+1 \sim m+n\)。此时考虑这棵树的 prufer 序列 \(p\)，显然有必要条件：

• \(\forall 1 \le i < n,\ 1 \le p_i \le n+m\)。
• \(1 \le p_n \le m\)。
• \(\forall n < i \le n + m,\ p_i = 0\)。

这确实是充分的，因为假设在 \(0\) 的儿子部分出现了 \(> n\) 的数字，那一定会在 \(p_n\) 或之前出现 \(0\)。所以显然这个问题的答案就是 \(m(n+m)^{n-1}\)。

这样绿色部分的答案就可以 \(O(\log n)\) 计算，前面的转移这样复杂度就来到了 \(O(nk \log n)\)，应该有 70pts。

显然这个 \(\log n\) 可以去掉，因为每次幂次都只改变 \(1\)，维护一下值时候乘上一个底数就好了，复杂度来到 \(O(nk)\)，应该有 80pts。

我们发现当 \(k \ge \sqrt n\) 时，转移只会形如 \([1,1] \to [2,i] \to [i+1,j]\)，其中 \(k \le i < 2k,\ j \ge k \lfloor \dfrac{n}{k} \rfloor\)。注意到此时转移显然只有 \(O(k^2)\)，由于同样可以维护幂次，所以此时复杂度就是 \(O(k^2)\)。至此有 100pts。