几个重要的偏微分方程（二）

热传导方程

问题提出：在三维空间中，考察一均匀、各向同性的物体G，假定其内部有热源，并且与周围介质有热交换，求物体内部温度的分布和变化规律。

任意一点(x,y,z)在t时刻的温度为u(x,y,z,t)。

方程推导：

能量守恒定律：物体内部因温度的变化而吸收的热量等于通过物体的边界流入的热量与由物体内部的热源所生成的热量的总和。

取空间中的一个空间微元D，先微分

t=t2时刻的热量：

 t=t1时刻的热量：

能量的变化，写成关于时间t的偏导数的积分。

以下求[t1,t2]时间段通过边界流入的热量:

由傅里叶热传导定律，即边界ds的热量dQ与物体温度沿曲面的法线方向导数du/dn成正比

积分

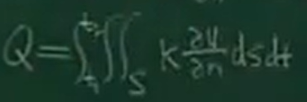
除了外部流入的热量，还需要求[t1,t2]时间段内部热源生成的热量：

设在物体G内热源的强度为F(x,y,z,t)，则由它生成的热量为:

由能量守恒，可得：

利用奥高公式，化解可得：

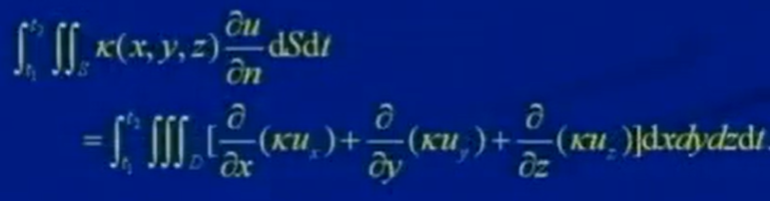
代入上面的能量守恒公式，可得：

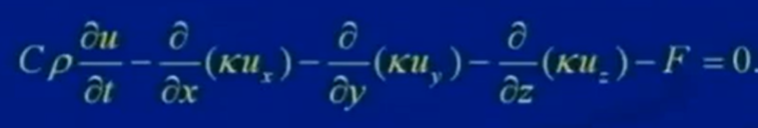
又物体是均匀的且各向同性，则C,ρ,κ都是常数，

令a²=κ/(Cρ), f=F/(Cρ)

则方程可化为

这是带热源的三维热传导方程。

如果物体内无热源或热汇，则方程为：

一维和二维热传导方程分别是: