几个重要的偏微分方程

1. 弦振动方程

问题提出：给定一根两端固定的拉紧的具有弹性的、均匀的、非常柔软的细线，其长为l, 在外力作用下在平衡位置附近作微小的横振动，求弦上各点的运动规律。

基本假设：
1.密度均匀
2.振动发生在一个平面，各点位移与平衡位置垂直
3.线是柔软的，不抵抗弯曲，张力与切线方向一致

方程推导：

动量定理：物体在某-时段内的动量的增量等于作用在该物体上所有外力在这一时段内产生的冲量。

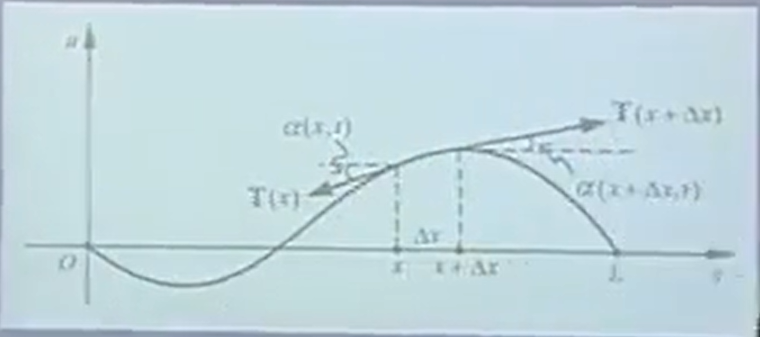
先求某一点的微分，再求整个线的积分。

张力，与时间无关。所以省略了t，只留下了x。求T(x)与T(x+Δx)的关系。

弹簧在每一点的张力大小与时间t无关，只与相邻的点之间的分子距离有关。被拉的越长，张力就越大。

按照胡克定律，一根长l的绳子，被拉伸了l+Δl。

已知y=y(x)是光滑曲线，求弧长ds。参考：

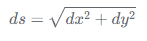
由于y是x的函数，即y=y(x)，那么dy = y'(x) dx。因此，代入上式：

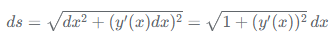
 由微弧长ds，可得某一段的弧长s。

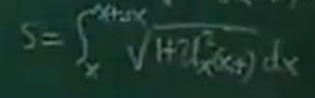
张力分为两个方向的力：x方向和y方向。

假设，平行方向x的力不存在，只存在垂直于x方向的y方向的力。

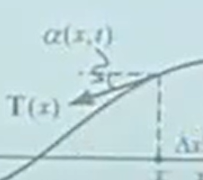
 力的分解。

可以写成

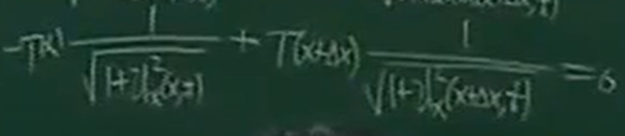
T(x)=T(x+Δx)

现在计算微弦段[x,x+Δx]上，t+△t 时刻的动量：

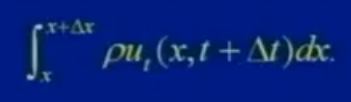
∫(密度*速度)dx

速度是指单位长度的切线速度还是垂直方向的速度？不重要，因为水平速度积分是肯定为0。

在t时刻的动量：

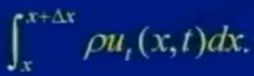
 根据动量定理，t+Δt时刻的动量减去t时刻的动量：

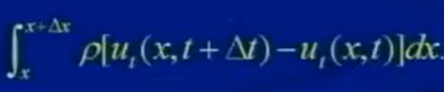
(绳子)动量的变化=(外界)垂直方向的作用力*Δt

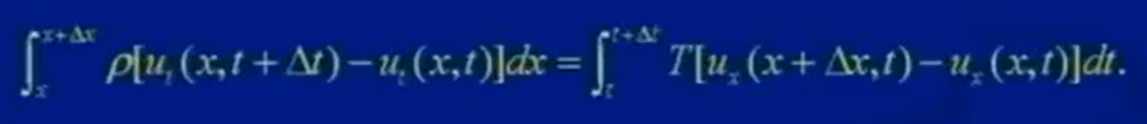
得

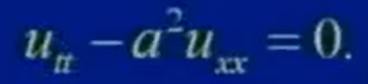
以上方程被称为一维波动方程，类似地可导出二维波动方程和三维波动方程，它们的形式分别为：

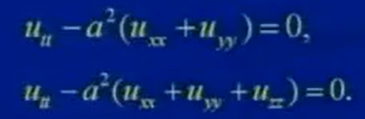
二维波动方程是指一个平面上的震动。

三维波动方程是指声音在三维空间中的传播。可以布满整个三维空间。