G. D-Function 题解 （快速幂， 组合数学）

原题链接：

https://codeforces.com/contest/1985/problem/G

题目：

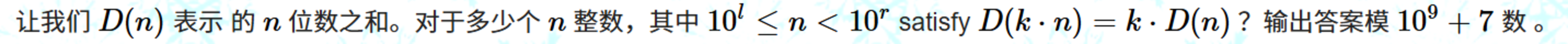
思路：

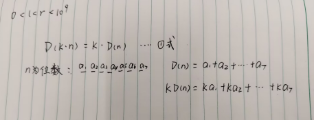
要满足D(kn)==kD(n), k与n的每一位相乘都不能发生进位， k只能是一位数。

考虑n的位数可能有1e9，所以用到了快速幂。

代码：

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int mod=1e9+7;
 
int fpow(int a, int n){//快速幂
    int ans=a, sum=1;
    while(n){
        if(n&1)sum*=ans, sum%=mod;
        ans*=ans;ans%=mod;
        n=n>>1;
    }
    return sum;
}
void solve(){
    int l, r, k;cin>>l>>r>>k;
    if(k>=10){
        cout<<0<<'\n';
    }
    else {
        int pos;//确定每一位有几个数满足要求。
        for(int i=1;i<=9;i++){
            if(i*k>=10)break;
            else pos=i;
        }
        int sum=fpow(pos+1, r)+mod-fpow(pos+1, l);
        //类似于前缀和， 不加mod可能会出现负数。
        cout<<sum%mod<<'\n';
    }
}
signed main()
{
    int T;cin>>T;
    while(T--){
        solve();
    }
    return 0;
}