FHQ-Treap
二叉搜索树(BST)
满足对于所有节点:
- 其左子树内所有的节点的键值,均小于其键值。
- 其右子树内所有的节点的键值,均大于其键值。
(图为一个二叉搜索树)
理论上来说,它的查找顺序是\(\log\)级别的,但是它可能被卡。
这样它的时间复杂度就炸了,所以我们就把它优化成了\(Treap\)。
\(Treap\)
\(Treap\)其实就是\(BST\)再加上一个优先级,每一个节点都有一个键值和一个优先级,键值满足\(BST\)的性质,优先级满足\(Heap\)的性质(即父亲节点的优先级小于子节点的优先级)
键值与优先级能够确定唯一的 \(Treap\) 形态(笛卡尔树)
\(FHQ-Treap\)
即无旋 \(Treap\),主要通过分裂和合并来维护平衡。
分裂:
将一个 \(Treap\) 分成 \(x,y\) 两个 \(Treap\)。
其中:
- \(x\) 中的值都小于等于 \(k\)
- \(y\) 中的点都大于 \(k\)
当 \(k=4\) 时:
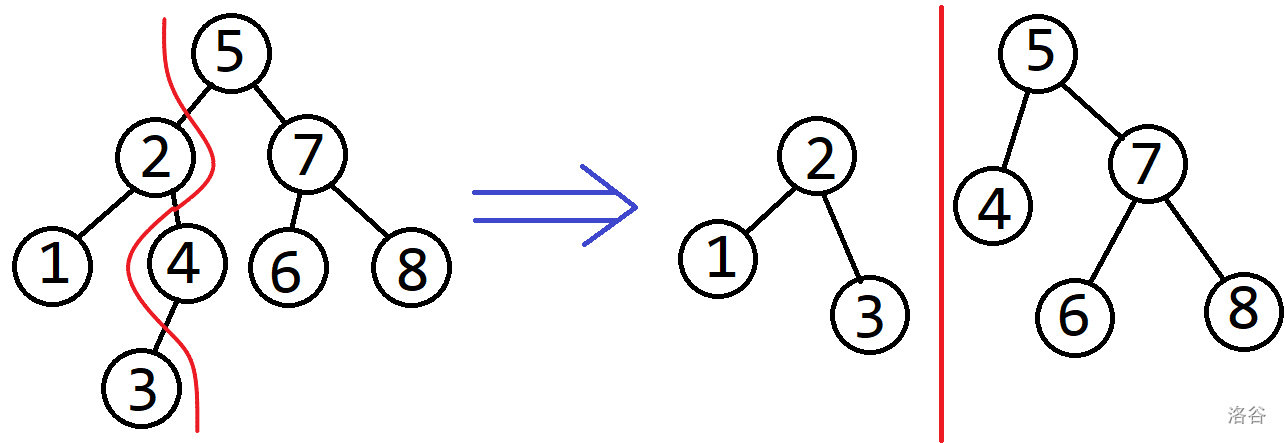
(上图数均为数值)
思路:
我们应用递归实现,比较当前树根和 \(k\) 的大小,并且相应的更新 \(x\) 和 \(y\),最后递归。
求法:
- 当前树的根的值和 \(k\) 比:
- 如果 \(\le k\)
- 使 \(x\)(即较小树的根)等于当前子树的根
- 分裂右子树
- 如果 \(>k\)
- 使 \(y\)(即较大树的根)等于当前子树的根
- 分裂左子树
- 如果 \(\le k\)
- 上传(即 \(pushup\))
\(code:\)
void pushup(int now){
fhq[now].size=fhq[fhq[now].l].size+fhq[fhq[now].r].size;
}
void split(int now,int k,int &x,int &y){
if(!now){
x=y=0;
}else{
if(fhq[now].sum<=k){
x=now;
split(fhq[now].r,k,fhq[now].r,y);
}else{
y=now;
split(fhq[now].l,k,x,fhq[now].l);
}
pushup(now);
}
}
合并:
将两个 \(Treap\) 按照权和大小合并成一个 \(Treap\)。
输入两个被合并树的根,返回合并后的根。
思路:
这里是以权值越大越靠近根合并的。
比较两树的根的权,因为在裂时 \(x\) 较小,\(y\) 较大,所以如果 \(x\) 的权大于 \(y\),那么合并 \(y\) 和 \(x\) 的右儿子,反之亦然。
我们发现递归容易实现。
求法:
- 比较两个树根的权,权大的作为权小的父节点
- 继续合并
code:
int merge(int x,int y){
if(!x||!y){//任何一棵树为空,返回另一棵树。
return x+y;
}
if(fhq[x].key>fhq[y].key){
fhq[x].r=merge(fhq[x].r,y);
pushup(x);
return x;
}else{
fhq[y].l=merge(x,fhq[y].l);
pushup(y);
return y;
}
}
插入:
给一个要插入点的值 \(sum\),把它插入到 \(Treap\) 里。
思路:
显然按 \(sum\) 把原树裂开然后把它们仨合并即可。
求法:
- 把原树按照 \(sum\) 裂开,裂成 \(x\) 和 \(y\)
- 申请新节点
- 把 \(sum,x,y\) 合并到一起
code:
mt19937 rd(114514)
int newnode(int sum){
fhq[++idx].sum=sum;
fhq[idx].key=rd();
fhq[idx].size=1;
return idx;
}
void insert(int sum){
int root_x,root_y;
split(root,sum,root_x,root_y);
root=merge(merge(root_x,newnode(sum)),root_y);
}
删除:
给定要删除点的值 \(sum\),删去一个点。
思路:
我们发现,把一个子树的左右儿子合并就相当于把根删掉,那我们把数值等于 \(sum\) 的子树拆出来,然后合并左右儿子再合并回去即可。
求法:
- 把原树按照 \(sum\) 裂开,裂成 \(x,z\)
- 把 \(x\) 按照 \(sum-1\) 裂开,裂成 \(x,y\)
- 把 \(y\) 的左右儿子合并
- 把 \(x,y,z\) 合并
code:
void delet(int sum){
int root_x,root_y,root_z;
split(root,sum,root_x,root_z);
split(root_x,sum-1,root_x,root_y);
root=merge(merge(root_x,merge(fhq[root_y].l,fhq[root_y].r)),root_z);
}
根据数值查排名:
给一个 \(sum\),求树中 \(sum\) 排在第几。
思路:
我们按照 \(sum-1\) 裂成 \(x,y\) 后记录 \(x.size+1\) 即可。
求法:
- 把原树按 \(sum-1\) 裂成 \(x,y\)
- 记录 \(x.size+1\)
- 把 \(x,y\) 合并
code:
int sum_to_rank(int sum){
int root_x,root_y,ans;
split(root,sum-1,root_x,root_y);
ans=fhq[root_x].size+1;
root=merge(root_x,root_y);
return ans;
}
根据排名查数值:
给定一个 \(rank\),求树种第 \(rank\) 个树是几。
思路:
我们从根开始找:
-
如果左子树大小大于等于 \(rank\),显然要求的值在左子树,就接着比左子树的子树和 \(rank\) 的大小。
-
如果小于 \(rank\),就比右子树的子树和 \(rank-\) 左子树 \(.size-1\) 的大小即可。
求法:
使用递推解决,下文 \(size\) 代指左子树 \(size\)
- 从根开始,重复判断左儿子的 \(size\) 与 \(rank\) 的大小直到当前的:
- 如果 \(size+1=rank\):
- 直接 \(break\),找到答案
- 如果 \(size\ge rank\):
- 把根设为左儿子
- 否则:
- 把 \(rank\) 减去 \(size+1\)
- 把根设为右儿子
- 如果 \(size+1=rank\):
code:
int rank_to_sum(int rk){
int now=root;
while(now){
if(fhq[fhq[now].l].size+1==rk){
break;
}else if(fhq[fhq[now].l].size>=rk){
now=fhq[now].l;
}else{
rk-=fhq[fhq[now].l].size+1;
now=fhq[now].r;
}
}
return fhq[now].sum;
}
求前驱:
给定 \(k\),求小于 \(k\),且最大的数。
思路:
直接找排名比 \(k\) 排名少1的数即可。
code:
int front(int k){
return rank_to_sum(sum_to_rank(k)-1);
}
求后继:
给定 \(k\),求大于 \(x\),且最小的数。
思路:
直接找比 \(k\) 大1的值的排行即可。
code:
int behind(int k){
return rank_to_sum(sum_to_rank(k+1));
}
例题:
code:
//#pragma GCC optimize("O2")
#include<bits/stdc++.h>
using namespace std;
mt19937 rd(114514);
struct Node{
int l,r;
int sum,key;
int size;
}fhq[100010];
int idx,root,n,m,ans;
int newnode(int sum){
fhq[++idx].sum=sum;
fhq[idx].key=rd();
fhq[idx].size=1;
return idx;
}
void pushup(int now){
fhq[now].size=fhq[fhq[now].l].size+fhq[fhq[now].r].size+1;
}
void split(int now,int k,int &x,int &y){
if(!now){
x=y=0;
}else{
if(fhq[now].sum<=k){
x=now;
split(fhq[now].r,k,fhq[now].r,y);
}else{
y=now;
split(fhq[now].l,k,x,fhq[now].l);
}
pushup(now);
}
}
int merge(int x,int y){
if(!x||!y){
return x+y;
}
if(fhq[x].key>fhq[y].key){
fhq[x].r=merge(fhq[x].r,y);
pushup(x);
return x;
}else{
fhq[y].l=merge(x,fhq[y].l);
pushup(y);
return y;
}
}
void insert(int sum){
int rt_x,rt_y;
split(root,sum,rt_x,rt_y);
root=merge(merge(rt_x,newnode(sum)),rt_y);
}
void delet(int sum){
int rt_x,rt_y,rt_z;
split(root,sum,rt_x,rt_z);
split(rt_x,sum-1,rt_x,rt_y);
root=merge(merge(rt_x,merge(fhq[rt_y].l,fhq[rt_y].r)),rt_z);
}
int sum_to_rank(int sum){
int rt_x,rt_y,ans;
split(root,sum-1,rt_x,rt_y);
ans=fhq[rt_x].size+1;
root=merge(rt_x,rt_y);
return ans;
}
int rank_to_sum(int rk){
int now=root;
while(now){
if(fhq[fhq[now].l].size+1==rk){
break;
}else if(fhq[fhq[now].l].size>=rk){
now=fhq[now].l;
}else{
rk-=fhq[fhq[now].l].size+1;
now=fhq[now].r;
}
}
return fhq[now].sum;
}
int front(int k){
return rank_to_sum(sum_to_rank(k)-1);
}
int behind(int k){
return rank_to_sum(sum_to_rank(k+1));
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
int a;
cin>>a;
insert(a);
}
int la=0;
for(int i=1;i<=m;i++){
int t,x;
cin>>t>>x;
if(t==1){
insert(x^la);
}
if(t==2){
delet(x^la);
}
if(t==3){
la=sum_to_rank(x^la);
ans^=la;
}
if(t==4){
la=rank_to_sum(x^la);
ans^=la;
}
if(t==5){
la=front(x^la);
ans^=la;
}
if(t==6){
la=behind(x^la);
ans^=la;
}
}
cout<<ans;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号