机器学习算法基本型 分类（笔记）

 

数据工作逻辑

1、定义问题对应的数据

• 原始数据集

• 通过各种方式获取，如公共平台、个人整理等

 

2、定义数据体现的特征，和数据之间的关系

• 根据数据集，你可以得到的一些特征，比如可用性、利润程度等

• 通过思考你的目标是什么，需要什么指标去衡量，指标即特征

 

3、数据分析。分为训练、开发和测试 （有时可以简化为2部分，比如 训练集:测试集=7：3）

• 训练集（training set）：训练模型的数据

• 开发集（dev set）：在开发过程中用于调参、验证（validation）等步骤的数据集（保证不被模型提前学习）

• 测试集（test set）：实际测试时所使用的数据集（保证不被模型提前学习）

 

4、根据测试效果，回到1和2步进行优化。不断迭代。

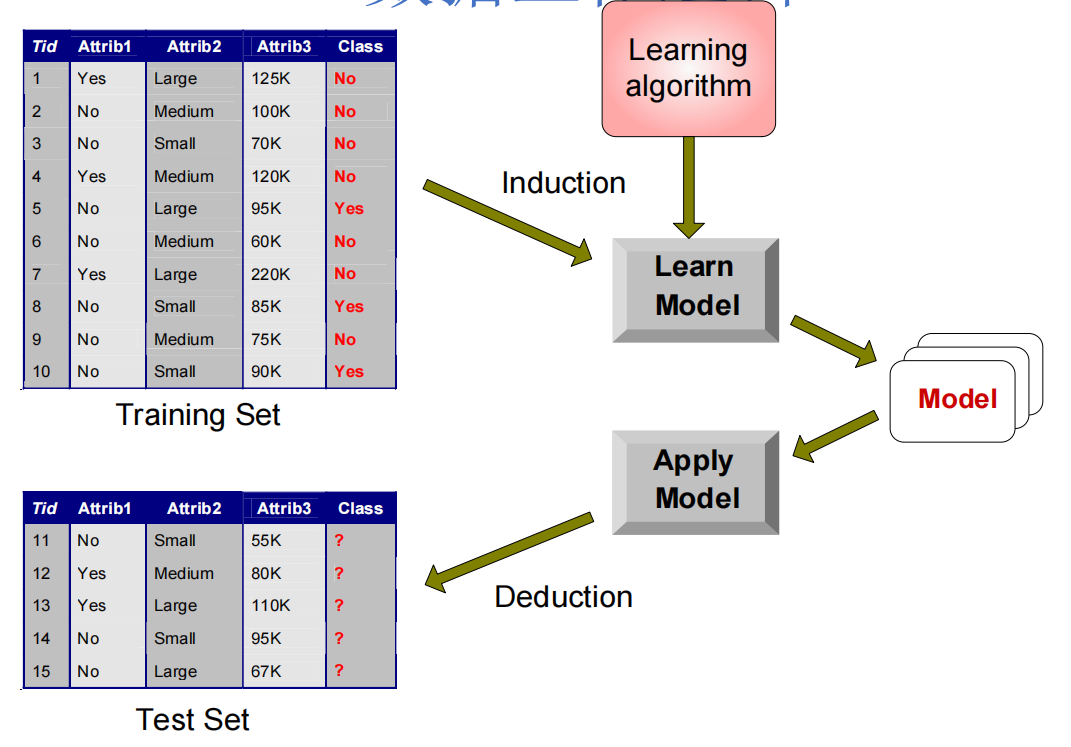
三个关键的误差水平

• 人类水平误差：假设，观察一张CT片子，不同的医生可能的误差是：普通医生误差10%，专家医生7%，一个专家组5%。这5%，就是现实世界的“最优可达到误差”的近似，也称为 “贝叶斯最优误差” 。理论上最低的误差，也不会低于这个值了；
• Avoidable bias（可避免偏差）：可避免偏差 = 训练集误差 - 人类水平误差。它衡量的是模型在训练集上相对于人类专家还差多少。这个值应该尽可能小，如果过大，就会欠拟合，需要通过对模型的调优（增加复杂度、调参数、训练再久一点等）来降低它；
• Variance（方差）： 方差 ≈ 测试集误差 - 训练集误差。它衡量的是模型从训练集到测试集的性能下降程度，这个值应该尽可能小，如果过大，就会过拟合。高方差意味着模型泛化能力差。

• 权衡关系：

  • 降低偏差（让模型更复杂）：通常会导致方差上升。

  • 降低方差（简化模型、正则化）：通常会导致偏差上升。

  • 我们的目标是找到最佳平衡点，使总误差最小。这种将avoidable bias和variance结合，就是机器学习领域的bias-variance trade-off（偏差-方差权衡）。

 Tips（没兴趣可跳过）：

1、贝叶斯最优误差：即使在拥有所有可能信息、做出最优决策的情况下，完成该任务仍然无法避免的最低错误率。它是由任务本身的模糊性决定的，而不是由学习者的能力决定的。比如上面的CT片子，可能由于图像质量、疾病本身的复杂性，或者信息的缺失，比如某些角度没拍到，导致这个任务本身具备一定的模糊性，你再提高自身能力，也一定会存在误差，这就是无法避免的错误。那和贝叶斯有什么关系呢？这是因为它的来源路径是：贝叶斯定理 → 贝叶斯分类器 → 贝叶斯最优误差。

1）从贝叶斯定理到最优分类器：以CT片子为例，根据这个片子，判断得癌症的概率，根据贝叶斯定理，可以基于“图像长成这样的概率（证据概率）“，以及“得癌症的概率（先验概率）“和“如果得癌症，我会有这种图像的概率（似然概率）”，得到得癌症的后验概率。即

P(癌症 | x) = [P(x | 癌症) × P(癌症)] / P(x)
= (0.3 × 0.01) / 0.031
≈ 0.003 / 0.031
≈ 0.0968 ≈ 9.7%

那么：P(正常 | x) = 1 - P(癌症 | x) ≈ 90.3%

此时，假设有一个全知全能的“上帝诊断系统”，它知道所有可能的概率，那它做决策，肯定是选择概率大的那个。比如，如果 P(癌症 | x) > P(正常 | x) → 预测癌症，否则 → 预测正常。上面的例子里，P(癌症 | x) ≈ 9.7%，P(正常 | x) ≈ 90.3%，9.7% < 90.3%，所以，在这种图像下，就可以判断，你没病，正常。那么问题就是，你没有上帝视角，你并不知道P(x | 癌症) ，也不知道P(癌症)、P(x)，这三个数据，本身的获取，存在误差。贝叶斯最优分类的意义主要在于，我假定你就是准确的概率结果，那我会怎么做决策，我的决策思路就是，谁概率大我选谁。它其实也隐藏了一个含义：如果你的估计足够准确，那你基于贝叶斯分类器大概率得到正确的决策（因为后验概率也不是100%，我只是让你选择错误率低的那个，也就是（1-后验概率）小的）。如果你概率就是错的，那根据我的分类器，你决策错了，这也不是我导致的决策误差。

2）从贝叶斯最优分类器到贝叶斯最优误差：理论上的贝叶斯最优分类器在实际应用时会犯的错误率。也就是P(error∣x)=1−max{P(C=1∣x),P(C=0∣x)}，选择了最大的那个概率，仍然可能犯错的概率。为了方便使用，通常使用P(error∣x)=min{P(C=1∣x),P(C=0∣x)}。然后把每个x对应的错误率，乘上x出现的概率，全部相加求平均，得到对应的错误率， 求平均，就是贝叶斯最优误差。比如：

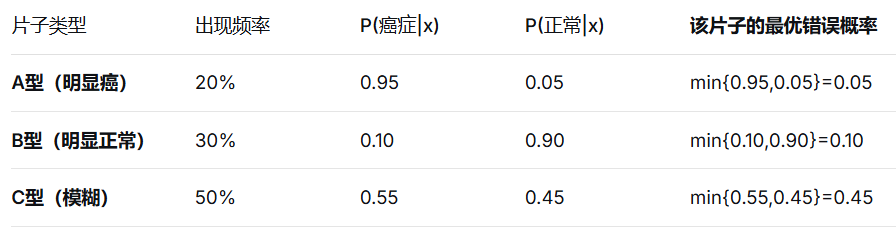
那么，总最优误差 = (A型出现频率 × A型最优错误概率) + (B型出现频率 × B型最优错误概率) + (C型出现频率 × C型最优错误概率)

                              = (20% × 0.05) + (30% × 0.10) + (50% × 0.45)
                              = 0.01 + 0.03 + 0.225
                              = 0.265 = 26.5%

 这个26.5%就是贝叶斯最优误差。

2、方差，数学上不是用来做稳定性的判断么？这里为什么又用来做误差的判断了呢？其实这是因为 期望误差=偏差²+方差+σ²，方差项确实会导致测试误差上升，高方差的模型必然在测试集上表现更差。既然，我能轻易算：测试误差 - 训练误差，那我就用“测试误差 - 训练误差”来代表“期望误差”吧。而期望误差，又和方差强相关。于是大家开始用“方差”指代“泛化差距”。可以理解为这是“方差”这个术语，在机器学习上的一个演化叫法。