建设项目经济评价的指标（笔记2）

 

笔记1，学习了各种经济评价指标和基准收益率的测定方法，例题主要以单一项目来示范。接下来会在具体的多项目评定中，继续理解这些指标是怎么使用的。

方案经济评价方法

评价方案类型

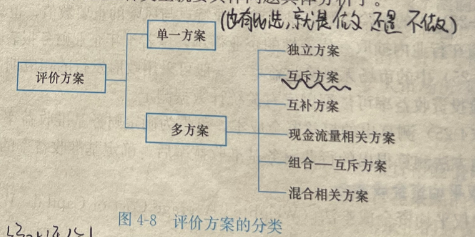
 这里面，最重要的，就是互斥方案，其他所有方案，都可以转化为互斥方案进行比较。互补方案，一般是出现在原材料和原材料的下游方案的组合情况。

独立方案经济评价

独立方案，实质就是在“做”与“不做”之间进行选择。因此，多方案的独立方案类型，与单一方案的评价方法是一样的。主要方法有：静态评价和动态评价。

静态评价

主要对项目的总投资收益率或静态投资回收期Pt进行计算，并与基准值比较，判断方案的经济效果。若投资收益率大于行业平均投资收益率，方案可行；或者投资方案的Pt≤Pc，说明能在规定时间内收回，方案可接受；

动态评价

主要用净现值NPV和内部收益率IRR进行评价。使用NPV时，NPV≥0，方案可行；使用IRR时，IRR＞ic，方案可接受。

互斥方案经济评价

互斥方案经济效果评价，主要包含两部分：

1、考察各个方案自身的经济效果，即进行绝对效果检验；

2、考察哪个方案相对经济效果最优，即相对效果检验。

两种检验的目的与作用不同，缺一不可。以此来确保，可行且最优。

具体评价方法主要有：静态评价和动态评价。

静态评价

通常用增量投资收益率（增量ROI）、增量静态投资回收期、年折算费用、综合总费用等评价方法。静态方案有极大的缺陷，但可以简单、直观地反应一些效果，方便汇报。

增量投资收益率法（增量ROI）

此公式，只能解决两两对比的情况。经常出现一种情况，某个方案投资额小，但总成本高；另一个方案投资额大，但总成本比较节省。这样投资大的方案和投资小的方案就形成了增量的投资。增量投资所带来的总成本费用上的节约与增量投资纸币，就是增量投资收益率。

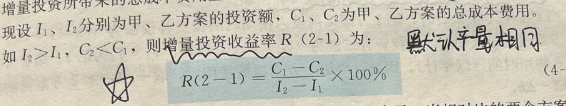
 若计算出来的增量投资收益率大于基准投资收益率，则投资大的方案可行，它表明投资的增量（I2-I1）完全可以用总成本费用的节约（C1-C2）来得到补偿。反之，投资小的方案为最优。

如果产量不同的两个项目比对，需要先把产量做单位化，了解一下即可：

可以参考如下例题，帮助理解：

 

 如果两个方案不是同时投入，需要加入投资补偿额，了解一下即可：

 

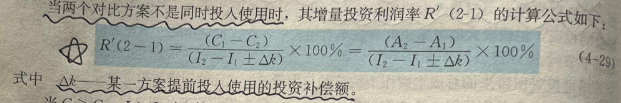
动态评价

常用的方法有NPV，IRR，NAV，NPVR等。

 上面这道例题，通过NPV计算，方案1优，通过IRR计算，方案2优。那么，要怎么选择呢？这时候要引入增值内部收益率。ΔIRR 的计算思路是：把 B 的现金流减去 A 的现金流，得到一组 差额现金流（注意，这个不是净现值之差。是每年的现金流之差），然后求这个差额现金流的 IRR。下面是一个计算的例子：

 

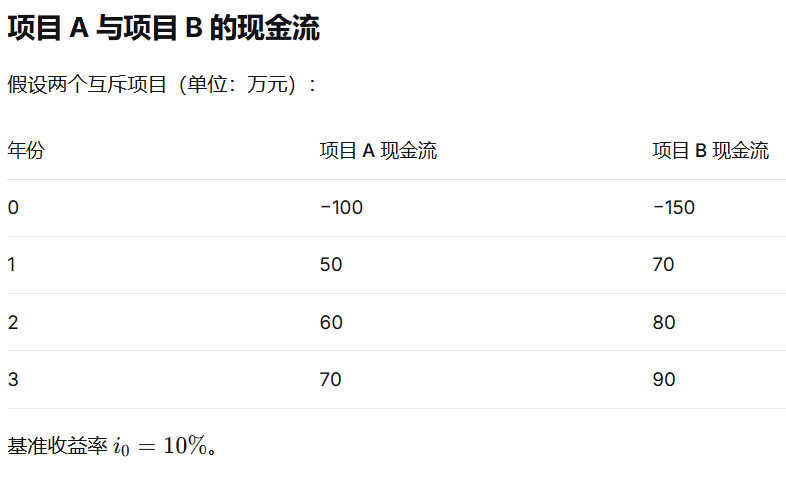
 计算出：ΔIRR ≈ 9.805%。

理解重点：ΔIRR 是比较 “多花的钱值不值” 的工具。ΔIRR 比基准收益率高 →选投资多的项目；ΔIRR 比基准收益率低 →选投资低的项目。此题计算后，ΔIRR>i0，与NPV结论一致。这时候如果调高基准收益率，使得增量IRR小于基准收益率，那就要选方案2.但此时NPV1<NPV2，IRR1<IRR2。因此 增量内部收益率的结论依然和NPV保持了一致。所以，最后结论就是，当 NPV 与 IRR 给出不同排序时，应以 NPV 为最终决策依据。

思考：那么，是不是要是对比选择哪个项目，我就计算NPV就行了，不需要再计算IRR了呢？不是的。即使两个项目的 NPV 已经计算好，IRR 仍然可能提供有用的补充信息。比如：

1）项目 A：NPV = 102 万元，IRR = 15%；
2）项目 B：NPV = 100 万元，IRR = 25%.

虽然 A 的 NPV 略高，但 B 的 IRR 显著更高，说明 B 的资金使用效率更高。如果公司资金有限，或者未来有更多投资机会，可能会选 B（用更少的钱赚更高的回报率，剩下的钱投别的）。所以我们在做决策的时候，最好提供绝对经济价值和相对经济价值两个角度，用于做最优决策。另外，△IRR和增量ROI的区别，这里就有一个非常明显的差异，就是△IRR是动态指标，衡量整个生命周期，增量ROI只看年平均收益差（两个项目总收益的差额/年份）和投资差的比值，是静态的。

 【解答】

一、NPV：

 由于两个方案寿命不同，所以在计算NPV的时候，有两种方法：

方法1：最小公倍数法。用最小公倍数法让两个项目的寿命一致。因此，对于方案A，计算3500的时候，第0年的投资就是-3500,4年后结束，需要重复投资3500，那就要把4年的那个3500折现，因此需要乘以复利系数（P/F,10%,4）。对于年金1255，n就不是4，而是8.对于方案B，正常计算就可以了；

方法2：取年限短的方案计算期作为共同的研究期。这里面要理解的是方案B怎么计算的。B的寿命8年，但我们只分析到第4年。那么在第4年末：

1）它已经运行了4年，获得了4年的收益：+1117 万/年；

2）它的资产并没有报废！设备还能再用4年，所以有剩余价值；

3）题目假设：第4年末的回收余值 = 固定资产残值（投资的30%） + 回收的流动资金200万。

因此，方案B在第四年末：

1）第0年：投资 -5000；

2）第1-4年：每年收益 +1117；

3）4年末：额外获得一笔资产回收现金 = 5000 × 30% + 200 = 1500 + 200 = 1700 万。

两个方法得到的结果是不一样的，寿命8年，选方案B，寿命如果定为4年，选方案A。那么这两种方法选哪个合适呢？它们不一致的核心原因是：

1）在8年视角下，方案B的长期收益（1117万/年，共8年）优势得以发挥；

2）在4年视角下，方案B的巨大投资（5000万）只用了4年就被迫“清算”，即使收回1700万残值，也无法弥补前4年收益较低的劣势（1117 < 1255）。

所以用哪个方法好，要结合项目背景（技术更新速度、产品生命周期、资产二手市场等），没有绝对“正确”的方法，只有适合特定决策情境的方法。

二、AW

AW，其实就是求NAV，这种术语混乱，和学术历史、学术习惯有关。

对于方案A，本身是4年，如果寿命为8年，投资3500万，每年收益1255万，4年后要重复投资。但要注意，AW法在这里自动处理了寿命不同的问题，因为(A/P)系数已经根据各自寿命计算了“年度化投资成本”。我们不需要像NPV法那样将A重复两次到8年。所以，AW(A) 的计算公式，不管是寿命4年还是寿命8年，都是：AW(A) = −3500(A/P,10%,4) + 1255 = 150.75万，具体理解如下：

1）-3500(A/P,10%,4)：将初始投资 3500万 分摊到它自己的寿命期（4年）中，变成 等额年成本；

2）+1255：每年的收益；

3）结果 150.75万 表示：在考虑资金时间价值、并考虑每4年重复投资的情况下，方案A 相当于平均每年净赚150.75万元。

对于方案B，寿命本就是8年的，结果不一样：

1）寿命8年：AW(B) = −5000(A/P,10%,4) + 1117 = 180万；

2）寿命4年：AW(B) = −5000(A/P,10%,4) + 1117 + 1700（A/F,10%,4）= -94.15万。

为什么会这样？AW不就是为了忽略寿命不同的情况吗？AW法确实能“忽略”寿命不同，但前提是——所有方案都在其“完整寿命周期”内正常运行，且分析目的也是考察其整个寿命周期。一旦我们人为设定一个“分析期”（如4年），并强制方案在期中终止，AW就必须考虑资产中断的损失，结果就会剧变。你也可以理解为，每个方案都在自己原定的寿命期里，每个方案的寿命期不同，这种时候计算AW，可以忽略掉寿命。那么方案A为啥4年，8年都一样呢？因为AW计算方法，已经隐含了“资产重置”的经济逻辑。已经考虑了资金的时间价值，并且隐含了一个假设——投资周期结束后，如果要继续运营，你需要重新借（投资）3500万。但要注意，4年和8年一样，但和5,6,7这种年份可不一样。只有是方案寿命的整数倍时，这种“AW值不变”的特性才严格成立。

 

三、IRR与△IRR

注意：

1）IRR先计算是否可行：IRR计算时，只看在一个投资周期内的收益情况，我们认为，每个周期的盈利能力是相同的（依然隐藏了一个条件：只有是方案寿命的整数倍时才可行）。所以方案A，哪怕用了寿命8年的前提，依然是计算第一个周期4年的收益。而NPV计算的是一个绝对的价值，必须要考虑全部寿命时间；

2）△IRR再计算谁更优：△IRR计算时，必须要拉到同一个寿命周期算，通常使用最小公倍数。计算的经济意义是，B比A多投资的这个钱，从内部收益率的角度看，值得不值得。另AW（B-A）= AW（B）- AW（A）= 0，计算△IRR。最后得到大于基准收益率，因此增加投资有意义，选B。

不同指标计算时，是否需要寿命一致？

 

寿命不一致推荐使用的指标