预测（笔记）

 

概念

利用历史数据，推断未来不确定因素的方法。这是基于：过去的规律，一定会在未来不断地发生。可以应用在销售数据、经济走势、产量范围、劳动力需求等。在项目PERT中，我们用均值、方差计算出某个时间完成的概率，这是一种预测方法，但并不适用于所有的预测情况。下图中，两个图像，他们的均值和方差，是完全相同的，但是从肉眼就可直接判断出，他们的密度并不相同：

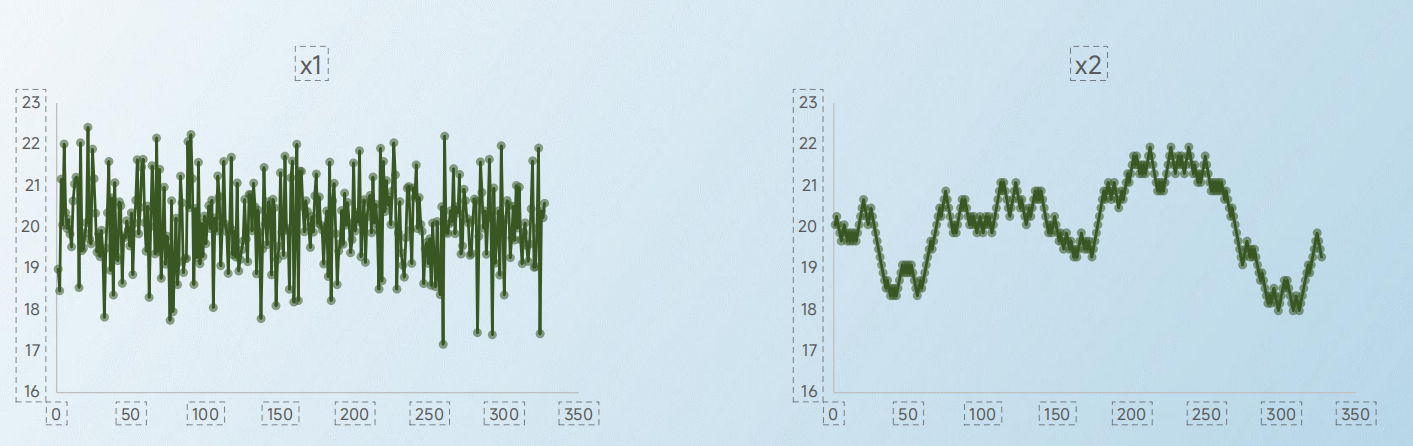
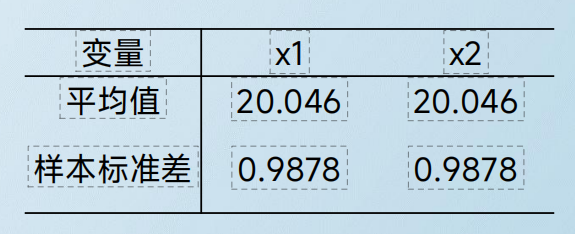
 这种情况，主要是由于左边的场景，是一种独立同分布的场景，比如扔骰子，每一次概率都是独立事件，每一次之间没有任何影响。这种时候，简单求历史均值、方差，可能不代表真正的情况；右边的图，则具有自相关性，因此，它会有一定的趋势变化，比如今天的价格，和昨天的是有关系的。

预测，我们通常采用的是，时间序列预测法。用一段时间的数据，预测下一个时间的数据。时间序列预测法有很多种预测模型，哪一种模型更适合某个预测场景，我们可以用以下几个参数来衡量：

1、 预测误差= |预测值-实际值|；

2、平均预测误差（MAD）：预测误差的平均值，这里主要是忽略较大较小的预测误差的差别，认为它们产生的影响是一样的。MAD=预测误差之和/预测次数；

3、均方差（MSE）：预测误差平方的平均值，主要突出较大的预测误差有什么样的影响。MSE=预测误差的平方和/预测次数；

4、季节因子：为某段时期内的平均数与总平均数的比值。它体现了数据在不同时期的波动情况。季节因子= 期间平均数/总平均数；

5、去季节因子：一段数据去除季节影响后计算的值，这个过程就是去季节因子。去季节因子=实际数据/季节因子；

在具体的预测模型应用时，求得预测值的步骤为：原数据→去除季节因子→预测→乘以季节因子→最终结果。具体如下：

1、拿到历史数据，做好分类分段；

2、计算分段的季节因子；

3、应用在原数据上，去季节化，即原数据/季节因子；

4、根据选定的预测模型，把每条历史数据重新进行预测；

5、将预测值*季节因子，得到最终预测值；

6、计算预测误差：|预测值-实际值|；

7、计算MAD、MSE，综合几种模型，选定最优、最适配的预测模型。

常用的几个excel方法：

1、绝对值：ABS（值1-值2）；

2、平均值：AVERAGE（表格范围）；

3、平方和：比如计算从H24到H34这些数据的平方和的平均值，就是SUMPRODUCT(H24:H34,H24:H34)/COUNT(H24:H34)。也就是自己和自己相乘相加后，除以数目。

 

时间序列法模型的应用

 某公司，近3年来，每个季度的呼叫量如下。

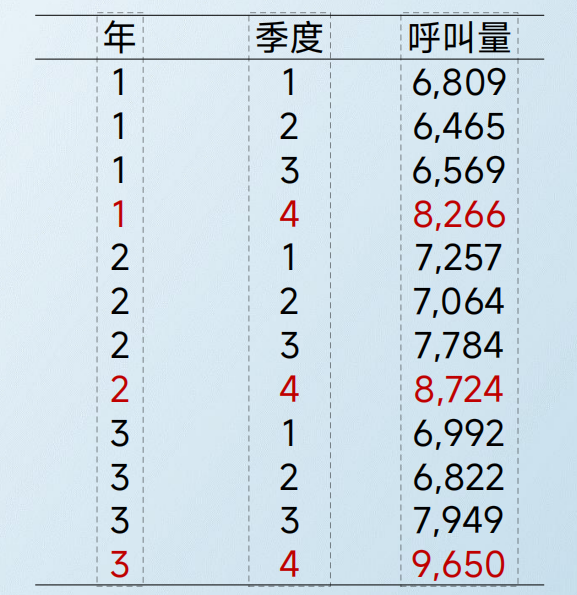
根据时间序列预测法，我们具体采用以下几种模型去解答。每种模型使用的情况如下表：

 

%25规则

%25规则预测模型。我们粗略估计各个季度的呼叫量，满足如下规则：

根据上述公式，在表格中列出预测量，进而计算出预测误差、MAD、MSE，如下：

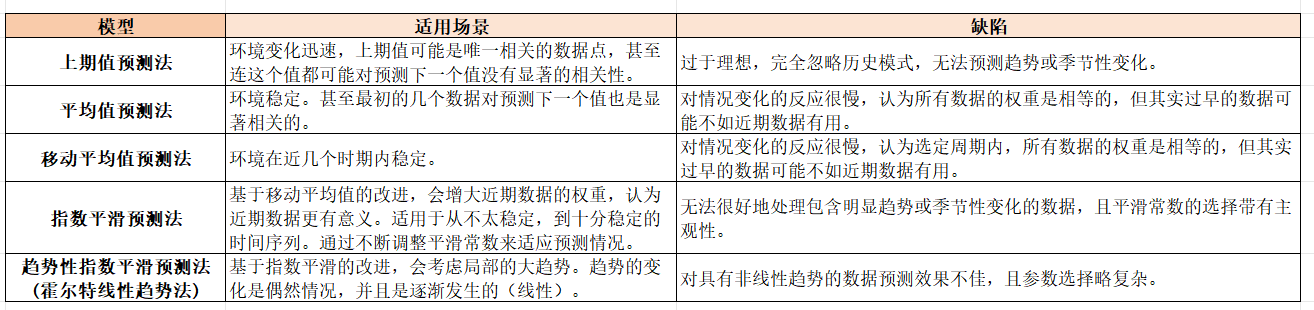
上期值预测法

预测值= 上期值，下图中，去季节上期值预测，第一年，第二季度的值，就是第一年第一季度去季节化的值。比如用昨天的价格，来预测今天的价格。上期值，忽略了除最后一个数据点以外的其他所有点。上期值预测法有时被称为天真的方法，但当环境变化迅速时，这个方法比较有效（上期值可能是唯一相关数据点）。

平均值预测法

用所有数据的平局值作为预测值。使用的是所有历史数据。这种方法适用于环境稳定的情况。对情况变化的反应很慢，认为所有数据的权重是相等的，但其实过早的数据可能不如近期数据有用。比如下图：

1、去季节上期值预测，第一年，第三季度的值，就是第一年第一季度和第二季度去季节化的平均值，也就是（7303.637+7175.559）/2，excel中用average；

2、去季节上期值预测，第一年，第四季度的值，就是第一年第一季度到第三季度去季节化的平均值，也就是（7303.637+7175.559+6653.167）/3；

3、依此类推。

 移动平均预测法

将与预测相关性高的最近若干期数据的平均值作为预测值。这种方法适用于环境在近几个时期内稳定的情况。对情况变化的反应很慢，认为选定周期内，所有数据的权重是相等的，但其实过早的数据可能不如近期数据有用。另外选取的时间窗对结果影响也很大。涉及两个关键定义：

1、时间窗 n = 被认为与预测下一个时期相关性高的最近的时期数，也就是决定一下用哪一段时间的数据来预测；

2、预测值 = 最近n个数据的平均值。

下图中，n = 4，代表使用前4个季度的去季节平均值作为下个季度的去季节预测值，之后*季节因子，得到预测值，进而求得预测误差、MAD、MSE。

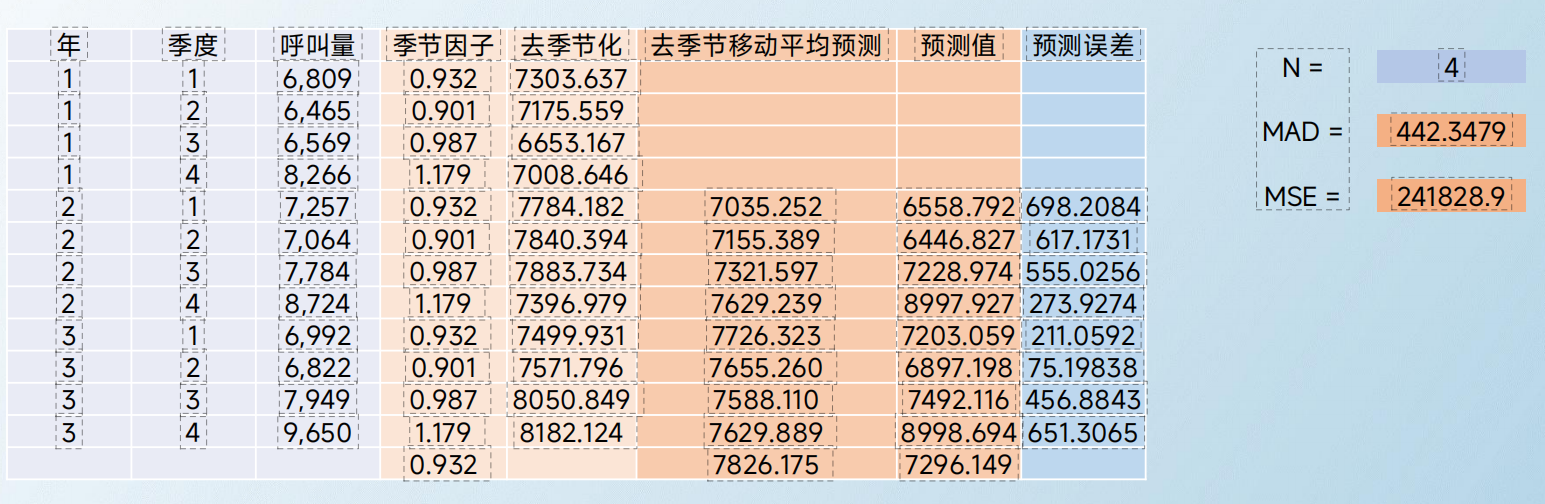
 指数平滑预测法

基于移动平均值的进一步改进。时间序列中，最近的值，赋予最大的权重，对较老的值赋予较小的权重。使用的数据是所有历史数据。较小的α适合相对稳定的情况（预测更平滑。认为历史数据中的误差都是随机波动，可降低关注。），较大的则适合于环境变化相对较快的情况（预测更为敏感，响应快。认为历史数据的误差主要来自于时间序列，也就是历史数据的浮动本身，需要提高关注。）。涉及两个概念：

1、平滑常数α：上期值的权重；

2、预测值 = α * 上期值 + （1-α）* 上期预测值。

注意：初始预测值可根据情况，直接取平均值或者上期值。

 

预测值的一般式推导，为了好观察，设置以下几个参数：

• Ft​ = 第 t 期的预测值；
• At−1​ = 第 t−1期的实际值，如果是At-2，就是往前2期的实际值；
• Ft−1​ = 第 t−1期的预测值，如果是Ft-2，就是往前2期的预测值；
• α = 平滑常数（0<α<1）。

1、根据公式，有 Ft​ = α⋅At−1 ​+ (1−α)⋅Ft−1​
2、根据Ft−1 ​= α⋅At−2​+(1−α)⋅Ft−2，代回Ft：Ft​ = α⋅At−1​+ (1−α) ⋅ [α⋅At−2​+(1−α)⋅Ft−2​]，展开得：Ft​ = α⋅At−1​ + α⋅(1−α)⋅At−2​+(1−α)²⋅Ft−2；

3、根据Ft−2 ​= α⋅At−3+(1−α)⋅Ft−3，代回Ft：α⋅At−1​+α⋅(1−α)⋅At−2​+(1−α)²⋅[α⋅At−3​+(1−α)⋅Ft−3​]，展开得：Ft​ = α⋅At−1​+α⋅(1−α)⋅At−2​+α⋅(1−α)²⋅At−3​+(1−α)³⋅Ft−3​；
4、继续递推展开，得到一般形式：

，直到 t-k = 0，也就是推导到初始预测值 F0.

所以可以看出，越靠前的数据，也就是越老的数据，权重越小。

 

实际在表格中应用此公式的时候，因为是从上至下的生成，所以每次表格的去季节预测值，都可直接使用公式 预测值 = α * 上期值 + （1-α）* 上期预测值，然后下拉，excel会帮助依次向下继续生成后续的预测值。之后*季节因子，得到预测值，进而求得预测误差、MAD、MSE。

 趋势性指数平滑预测法

基于指数平滑进一步的改进。除了季节因素，可能时间序列中，还存在局部或者全局的某种趋势，比如某短时间，由于货币政策，会对数据有宏观影响。引入新的参数：趋势平滑常数β，0<β<1。首先估计当前向上或者向下的趋势，结合此趋势估计，进一步得到预测值。涉及的概念：

1、趋势：假设目前模式会持续，时间序列从一个值到下一个值的平均变化；

2、上期趋势 = α⋅上期值的变化值 + (1−α)⋅上期预测值的变化值;

3、趋势估计 = β * 本次所求的上期趋势 + (1-β）* 上期趋势估计;

4、预测值 = α * 上期值 + （1-α）* 上期预测值 + 趋势估计；

注意：

1）初始预测值可根据情况，直接取平均值或者上期值；

2）初始趋势估计可根据情况取平均值或上期值或零等。

 

在表格中应用的时候，需要增加“上期趋势”、“趋势估计”这两个参数列，对应表格公式，以第一年，第二季度为例（只能从此行开始，因为第一个上期趋势，就需要上期的变化差值。）：

1）上期趋势 = α⋅（第一年第一季度的呼叫量 - 初始预测） + (1−α)⋅（第一年第一季度的去季节预测值 - 初始预测值）;

2）趋势估计 =  β * 第一年第二季度的上期趋势 + (1- β）* 的趋势估计;