非线性规划（笔记）

概念

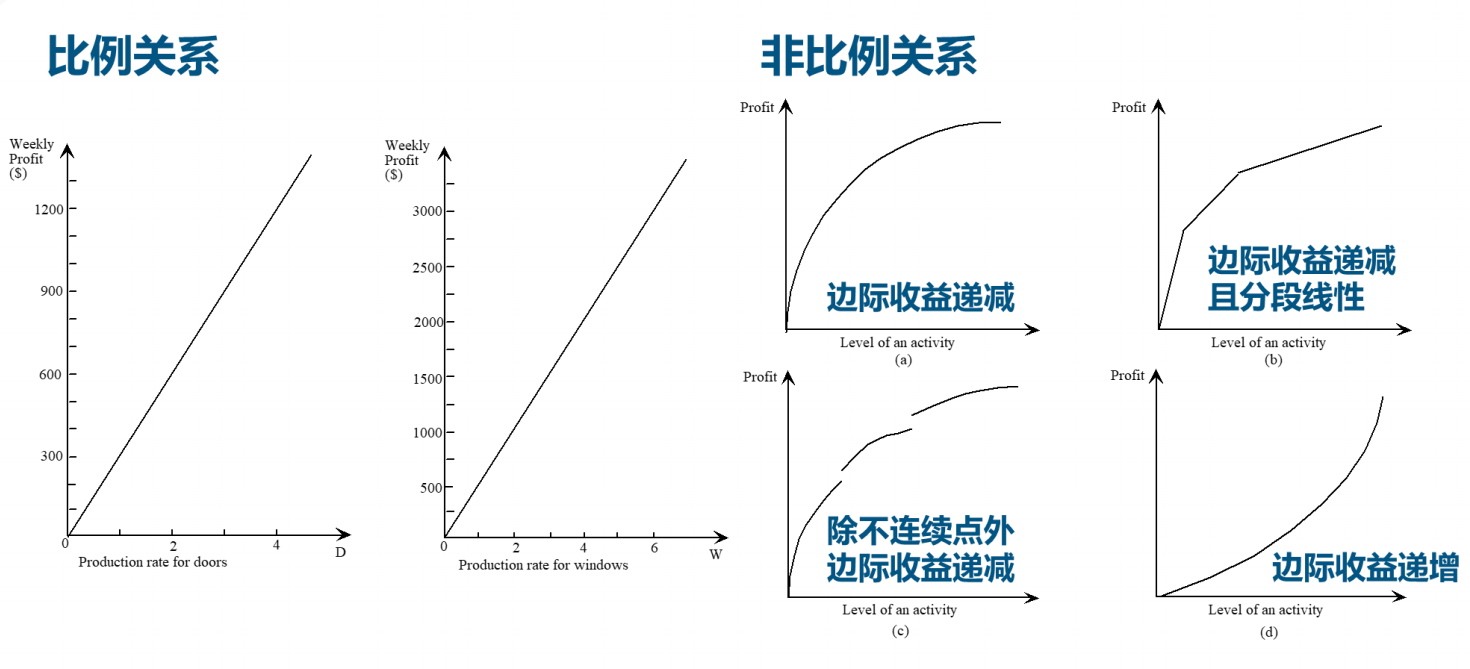
在一些实际的问题中，决策的变量和目标函数，很可能并不是线性变化的，对这类问题做规划，就是非线性规划。它比线性关系复杂，求解的模型也更加复杂。只要任一决策活动与目标函数之间，存在非比例关系，那么就会产生非线性规划问题。具体的图形对比，可以参考下图。

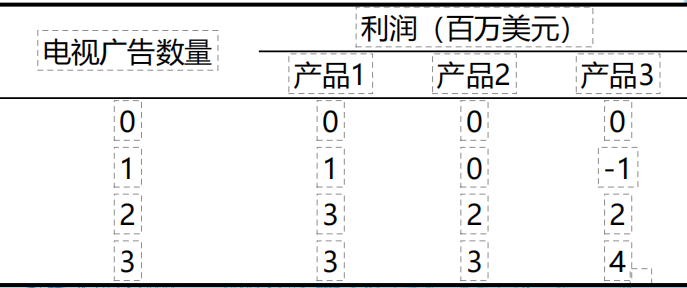
比如，某公司购买了5个广告片，对3种产品进行促销。每个广告只针对1种产品，每种产品最多可以有3个广告，最少可以不做广告。如何将这5个广告分配给3种产品呢？以下是每种产品，当有0个、1个、2个、3个广告做促销时，分别获得的利润情况。这就是一个明显的非线性情况，利润并不总是跟着广告数目的变化而持续增长/下降，而是忽上忽下。

 

 举例

【例1】给出一些离散点，怎么去判断，它的最大值呢（y轴）？ 下图是一组先验数据（历史记录、实验、估计），说明了水平和利润的一些数据情况。

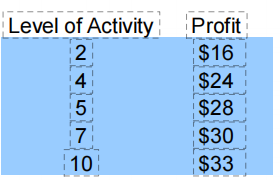
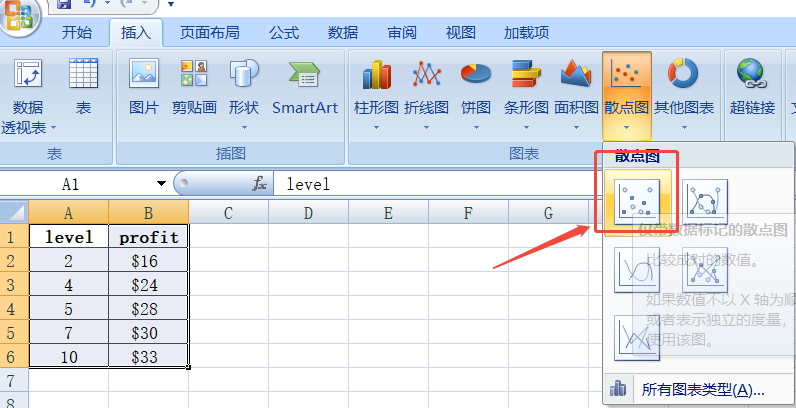
1、首先，要找到符合它规律的公式，这个公式不会保证每个点都在图像上，但它可以足够贴合这些点的出现可能。在excel中，可以先把这些离散的点，画出来，然后再选择最近似的公式曲线去拟合它。选择不同的公式，拟合的情况也不相同。

 

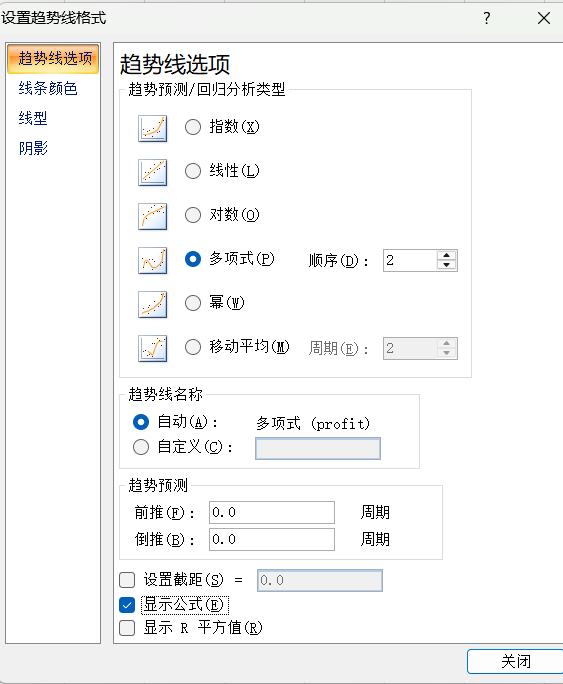
 经过多次比对，选择多项式，2次，显示公式，可以得到下图中，一条足够贴合这些点的曲线。次数越高，图形会更加拟合：

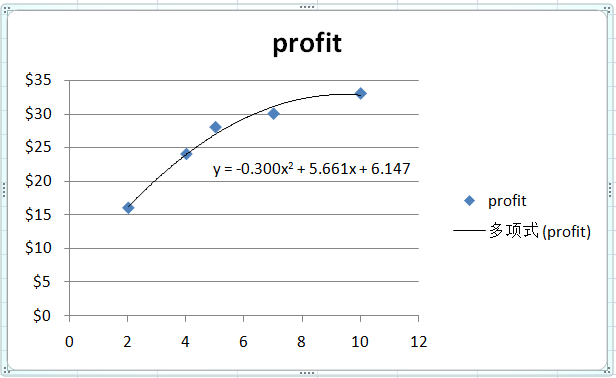
 【例2】现在来看另一种情况。此时用excel规划求解如下公式代表的最大利润，注意不要勾选线性规划。我们分别约束x的最小值，来达到模拟从不同数值出发，可能得到的最大值，发现从0开始、从3开始、从4.7开始，虽然x的最大值都是5，但是最大值并不相同，这是为什么呢？

 主要原因，是因为，这个公式表示的，是一个起伏并不规律的图形。虽然整体图像是这样的：

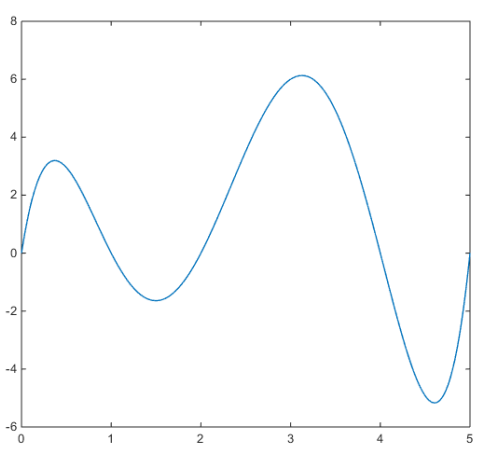
 但是从0出发，会先上升，然后就会下降。一直走一直下降，直到达到1-2中间，才有上升。此时你被起伏整懵了，到底什么时候，才能有我的最大利润？从3出发，你会发现，一直走，一直下降，根本没有上升的希望。这时你想要放弃。算了吧，增加x只会带来亏损。但如果再坚持一下，一直走，一直走，走到4到5之间，这时候其实就会上升了。但你是不是一定会坚持呢？从4.7出发，你会发现你会一直上升，你以为你只要不断努力，你就可以得到最大的利润。你觉得，这个世界真是无比美好，努力就有收获。

但，开了上帝视角的出题人，其实能够从图形中看到真正的最大利润，以及你的每一次努力是否有意义。

从不同的起点出发，你看到的世界，形成的观点，并不相同。这需要我们打起精神，更小心地进行决策。

【例3】某公司，制作一扇门的利润是375，制作一扇窗的利润是700。假设制作D个门，W个窗。营销门的成本是25D²，窗营销成本是（200/3）W²。三个工厂制作，每个工厂分别可以使用的工时如下。问，制作多少门窗，可获得最大利润。

 解答：

1、目标函数：max利润=375D+700W-25D²-（200/3）W²；

2、约束条件：

1）D≤4；

2）2W≤12；

3）3D+2W≤18；

4）D,W≥0.

3、这个决策条件，确实是线性的，但是目标函数，是非线性的。根据图像法，可以看到，最值，和线性规划不同，不会出现在节点，而是出现在一条边上：

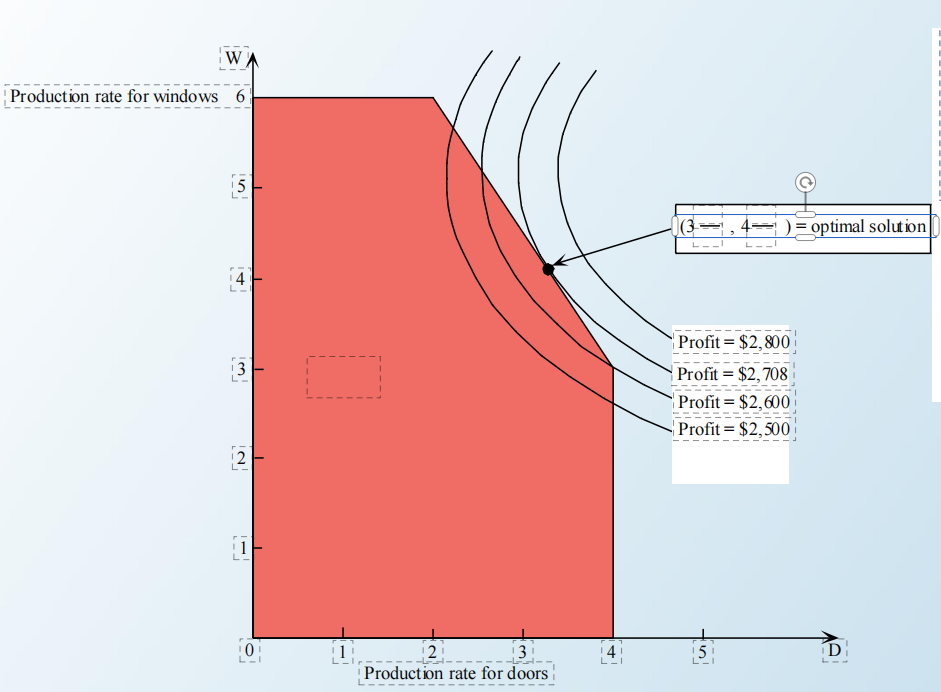
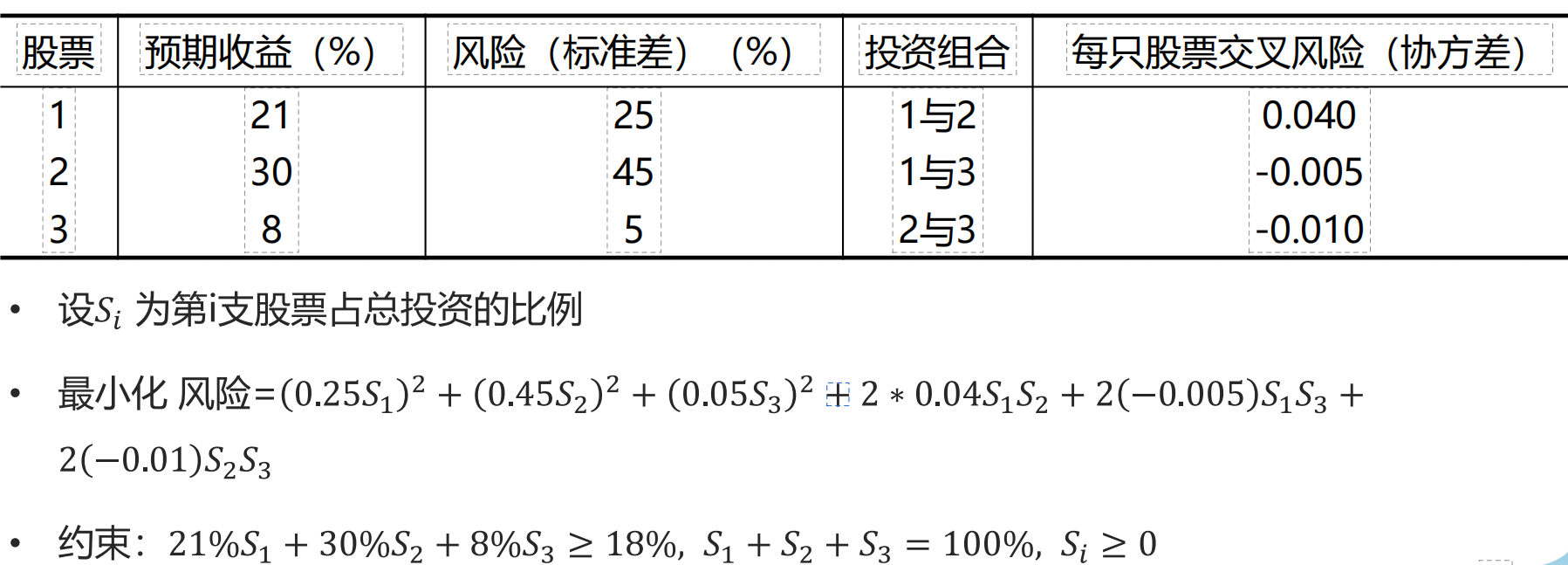
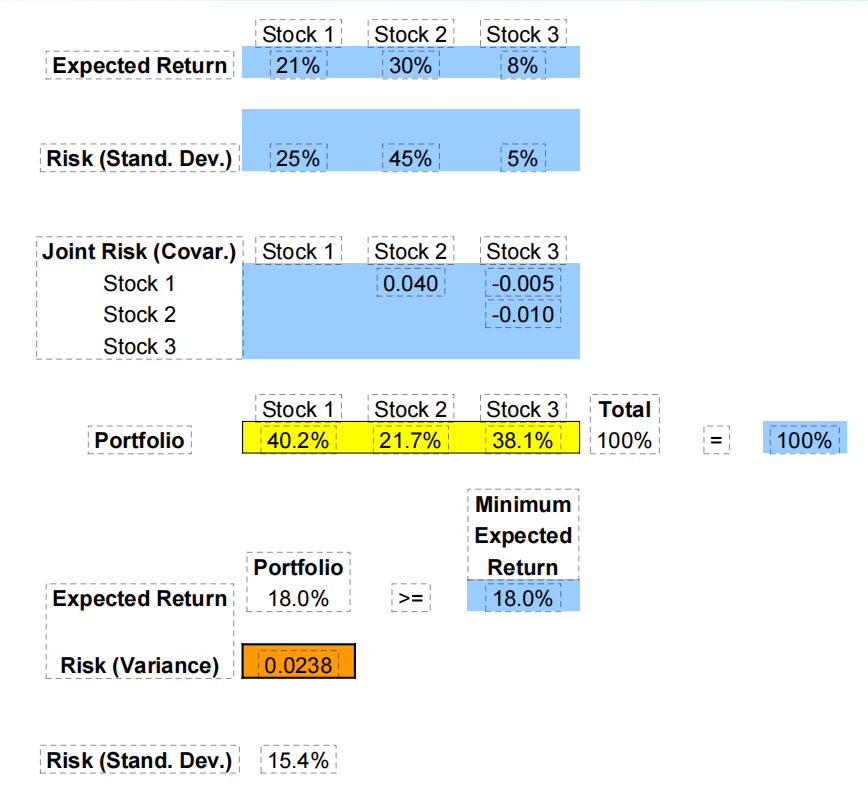
 【例4】三种证券做投资组合，数据如下表。怎么组合，可以让预期收益超过18%的情况下，风险最小呢？具体可以使用以下公式，进行非线性规划。这里我就不分步骤了

 

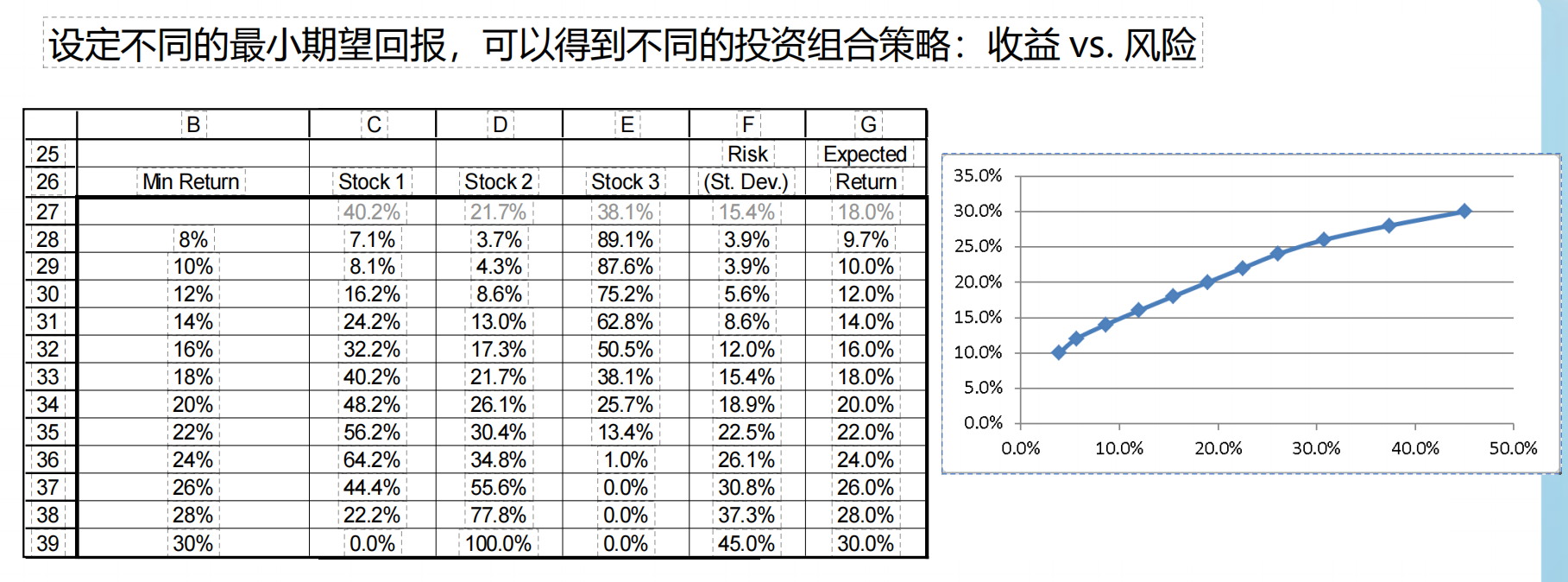
 进一步，我想知道不同的最小期望汇报，对应的风险和收益。可以用solver table得到。帮我做更多的分析和预测，做出最优决策。

 其他思路求解非线性规划

可分离规划

非线性规划的复杂度是比较高的，但是如果可以对非线性的图形，通过分段，分成一段段线性规律的图像，再用线性规划求解，是不是能使得问题变得简单一些呢？答案是，如果目标函数满足分段线性+边际收益递减，那么可以使用线性规划。将非线性转化为线性规划，主要是为了降低求解复杂度，加快求解。并且也可以得到敏感性分析报告。

【例1】某公司，从工厂1和工厂2调出一部分工人做其他事情，这时，为了最大限度利用每个工厂的机器，剩下的工人必须要加班。但加班会导致成本增加，也会降低单位利润。工厂3由于没有人力变化，不受影响。那么这种情况下，一周生产多少门窗是合适的呢？

 解题：

1、先分别看生产门、窗的图像。由于正常时间的生产获得的利润，肯定是优于加班时间生产的利润，因此，符合边际收益递减。同时，分段也符合线性规律。所以尽力先把正常时间的生产数量做满，再做加班的。比如门生产3个，利润是 正常时间生产一个门的利润*3，如果生产4个，就是正常时间生产3个，加班时间生产一个，就是300*3+200*1.

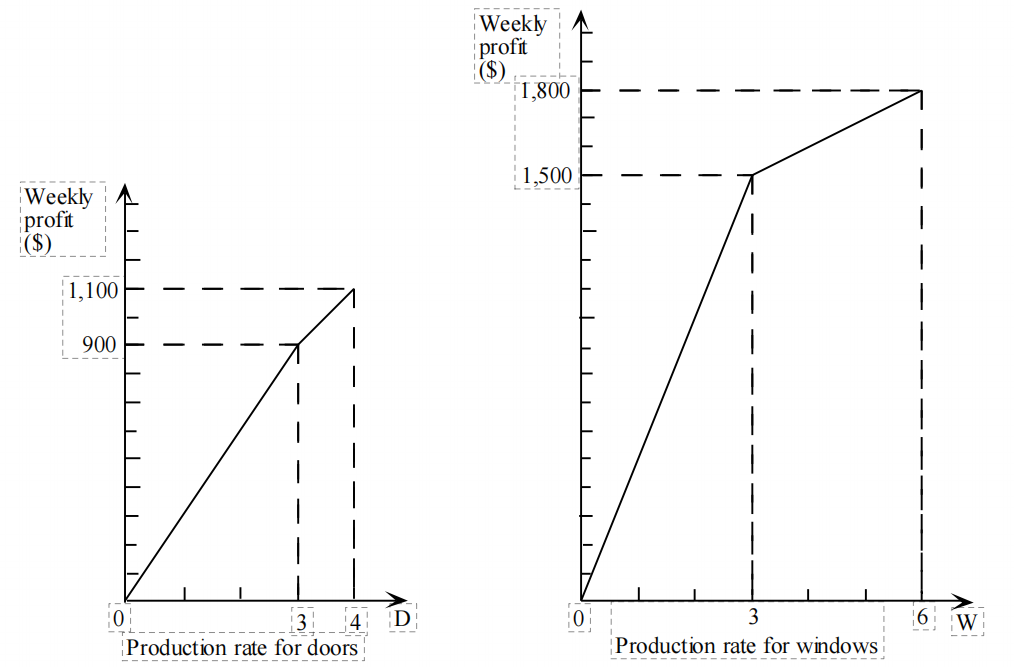
 2、分离规划条件，写出目标函数，以及约束条件；

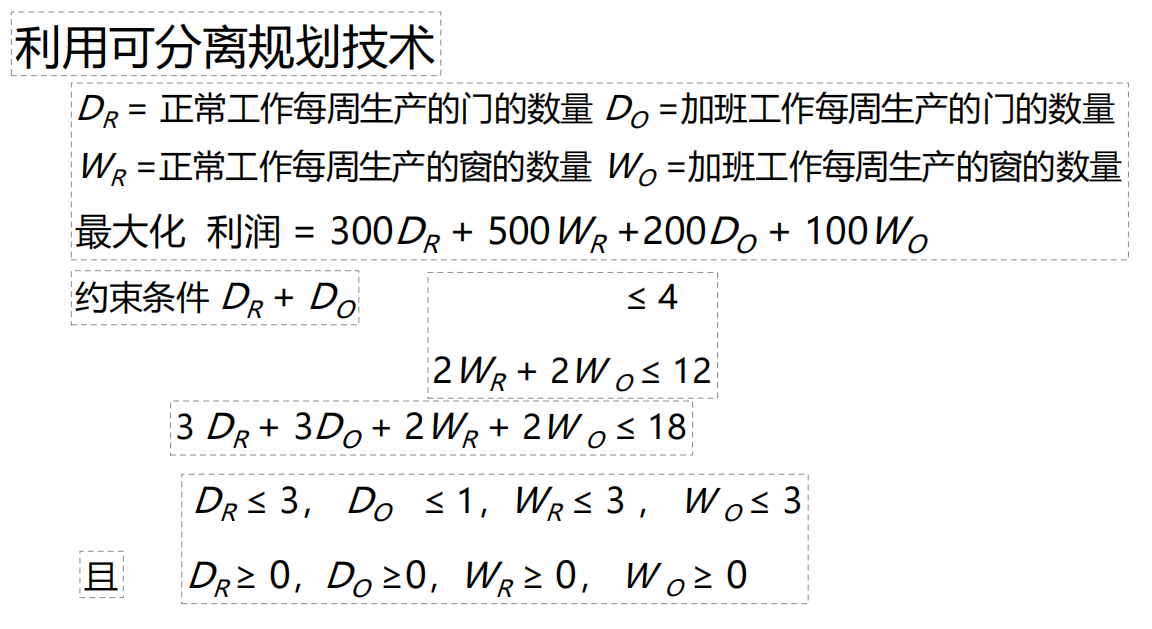
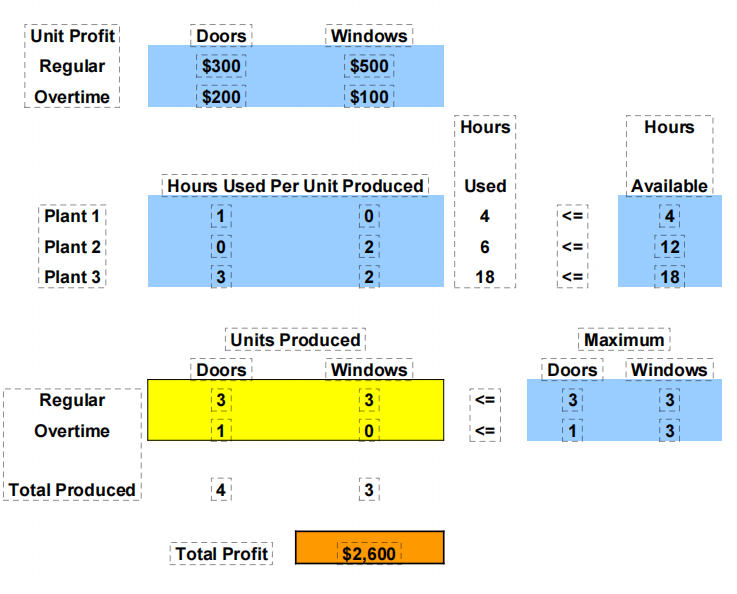
 3、计算结果。

 近似可分离

当利润函数为光滑曲线时，可以将它近似为分段的线性函数，然后再利用可分离规划近似计算。将一段曲线，转为近似的直线，就无需大量数据去做曲线拟合了。

【例1】上题，如果继续增加条件，还有营销成本，那么根据我们之前的模型，营销成本部分是二次函数，是一段曲线，我们就可以考虑把它线性化。

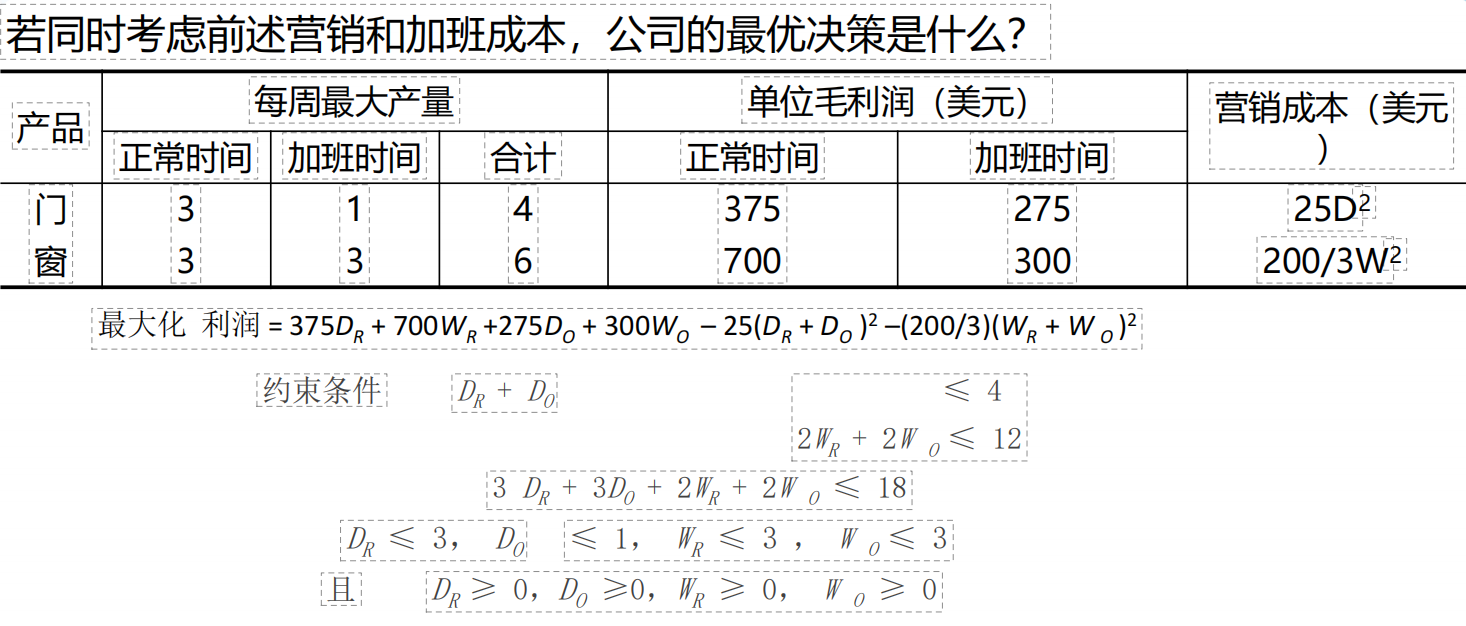
 solver table后，可以得到一组变化数据。可以看到窗户再生产4个开始，就不划算了，利润就负数了，所以就不用继续关注了：

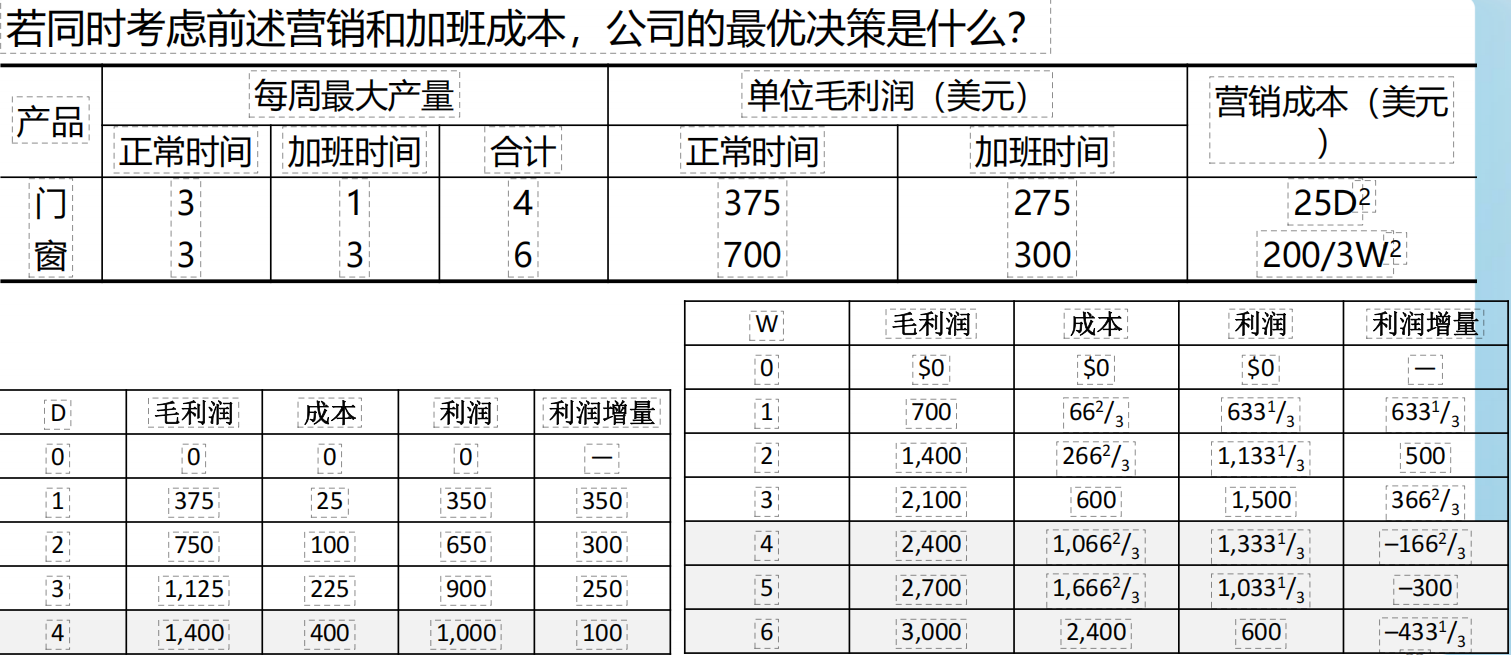
 所以，我们近似将这个目标函数，按 正常时间生产0-1个门、窗（门、窗分别最大值只能是1），正常时间生产1-2个门、窗（门、窗分别最大值只能是1），正常时间生产2-3个门、窗（门、窗分别最大值只能是1），加班生产来分开进行计算，相当于转为了分段的线性规划。最终求解如下，左边为利润增量，右边为利润。基于左边得到门窗在生产时间和加班时间的个数，再结合右边得到利润。最后减去营销成本的1000元，得到最终利润2500元：

 复杂的非线性规划问题

上面的门窗示例，主要是目标函数为非线性。如果决策活动也是非线性的，继续使用规划求解会非常困难。这时候可以使用“多初始点”进行求解。也可以考虑遗传算法。