网络优化问题

 

一、基本概念

【发点和收点】设点 v 是有向图 D （带箭头）的一个顶点：

1、发点：如果不存在以v为终点的弧，则称v是D的一个发点(源），通常称为vs；

2、收点：如果不存在以v为始点的弧，则称v是D的一个收点(汇），通常称为vt。

【容量和流量】

1、容量：网络中某条弧（vi，vj）的最大通过能力称为该弧的容量，记做 cij ；

2、流量：通过弧 （vi，vj）的某种流的实际数量称为该弧的流量，记做 fij 。

【可行流和最大流】

发点 vs流出的流量为 f ，则汇入收点vt的流量为 -f。这个f，就是可行流。如果一个网络图中，有n个发点，n个收点，那么可行流就是所有发点发出流量的和，也就是所有收点收到流量的和。

 

可行流具备以下两个特征：

1、可行性条件：对每一条弧 （vi ， vj ）∈ A ，均应有，0 ≤ fij ≤  cij。即每条弧的流量，都应该是非负的，是大于等于0，且小于这条弧的容量的；

2、平衡条件：除了发点和收点，其余点都是中间点，可以理解为中转站。流入任何一个中间点的流量必等于流出该顶点的流量，即对 vi ≠ vs , vt时：

 。

 

 

因此对于可行流 的流量 f 来说，对于每个节点，它的公式就是如下形式。发点，则无目标为自己的收流量，就是 减去0，因此 f 也就等于发点发出的所有流量，对于收点就是 -f。如果这个f有最大值，就是最大流，计算最大流的时候，可以简单只sum发点的流量。具体最大流概念下面会再进行解释 ：

 

 示例：下面的网络图，每个弧，弧旁第一个数字为容量，第二个数字为流量，即 cij， fij。这个网络图里的流，是否是可行流呢？每条弧都满足非负性和中间点的平衡条件，因而为一可行流，且可行流 f = 6（发流量为2+4）。这里有一个特殊的情况，即，可能存在某条弧完全没有启动，或者整个网络为初始状态，这时候就会有零流 fij= 0，它一定是一个可行流。因而在一个网络图中，可行流总是存在的，至少有零流。

 

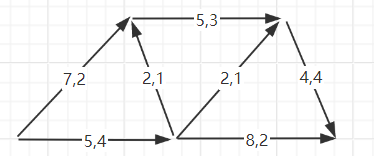
 【网络的最大流】

在一张网络中，每条弧容量不同，如果不计成本，尽力而为地传输，不同的规划，得到的可行流的流量，并不相同。找到最大的可行流，也就是找到网络的最大流，是很多实际问题需要的。这也是一个线性规划问题，可描述为：

 

二、具体问题

 【最小费用问题 （运输和指派问题，供和需都有明确的要求）】

有两个工厂生产产品，这些产品需要运到两个仓库里．工厂１生产８０个单位，工厂２生产７０个单位，仓库１需要６０个单位．仓库２需要９０个单位，工厂１和仓库１之间以及工厂２和仓库２之间有一条铁路运输轨
道（铁路上的运输量没有限制），卡车司机总共可以从工厂运输５０个单位到配送中心，然后可以从配送中心运输５０个单位到仓库。

问题：每条路线运送多少单位的产品使运输成本最小？

  【解题】

具有可行解的特征：在以上的假设下，当且仅当供应点所提供的流量总和等于需求点所需要的流量总和时，最小费用流问题有可行解；

具有整数解的特征：只要其所有的供应、需求和弧的容量都是整数值，那么任何最小费用流问题的可行解就一定有所有流量都是整数的最优解；

1、网络构成：

1） 节点涉及供应点、需求点、转运点；

2） 弧涉及容量、单位成本。

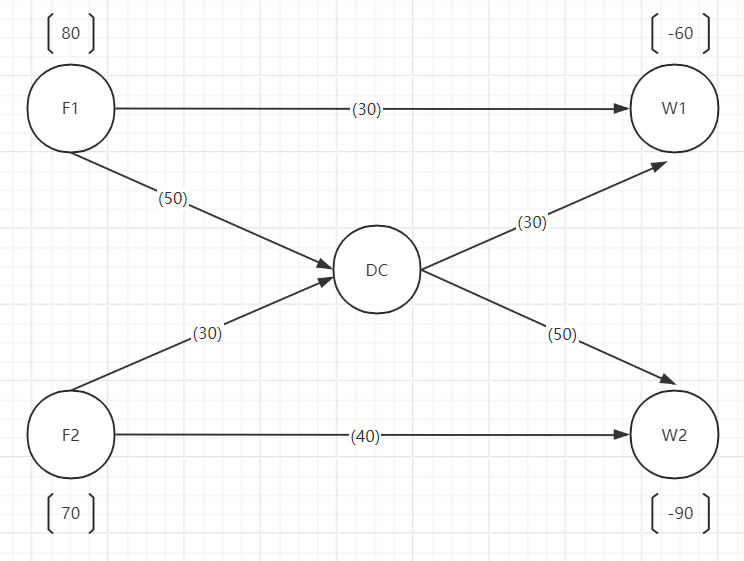
2、目标函数：成本=选定的道路*对应的单位成本；

3、约束条件：

1）每条弧的流量≤容量；

2）转运点，没有需求，所以是0。也可以理解为 中间点的 进流量 = 出流量 ；

3）开始节点的流量 = 供应量；

4）结束节点的流量 = 需求量（注意，为负数）。

3、列表，规划求解：

 

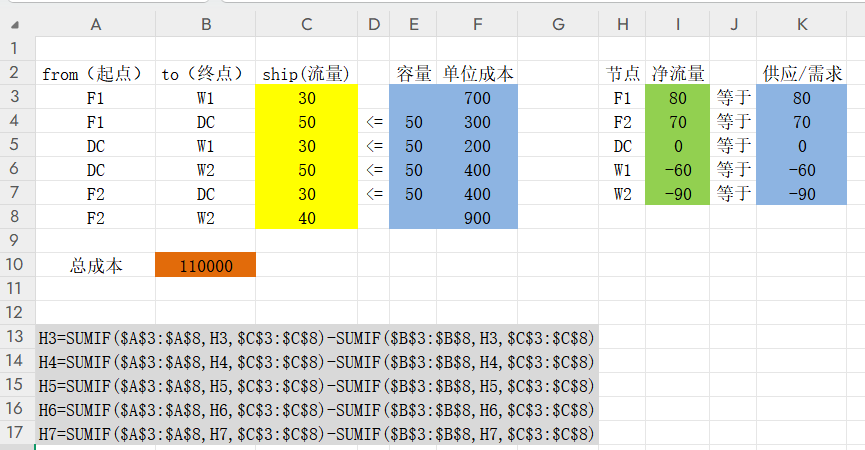
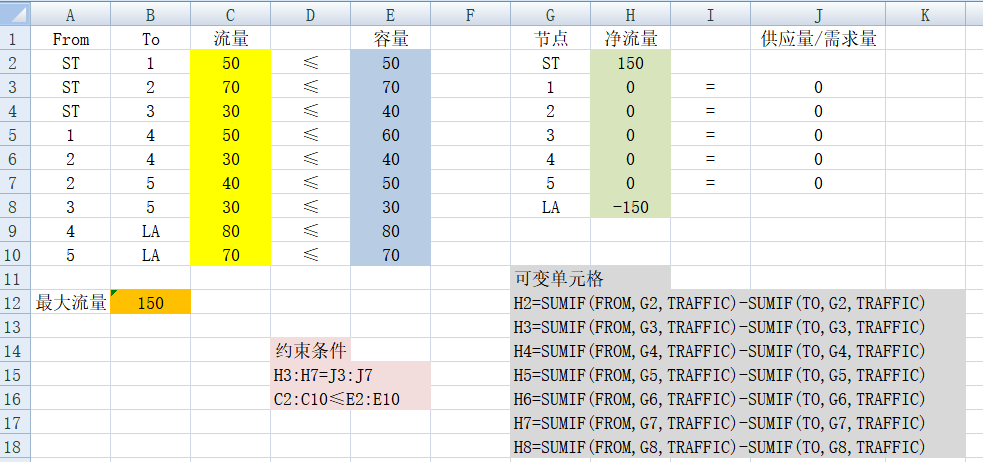
 【最大流问题（无明确的供需数目，是尽力而为的传输。起点、终点的供需不设限）】

一家汽车公司，需要制定一个方案，使得下个月从总厂运送到洛杉矶配送中心的供应件尽可能多，可以运送多少配件的限制条件就是该公司配送网络的容量。

问题：通过每条运输路线可以运送多少单位的货物，使得斯图加特工厂到洛杉矶配送中心的运输单位总量最大？

【解题】

1、网络构成：

1）节点：源、目的、转运点；

2）弧：容量。

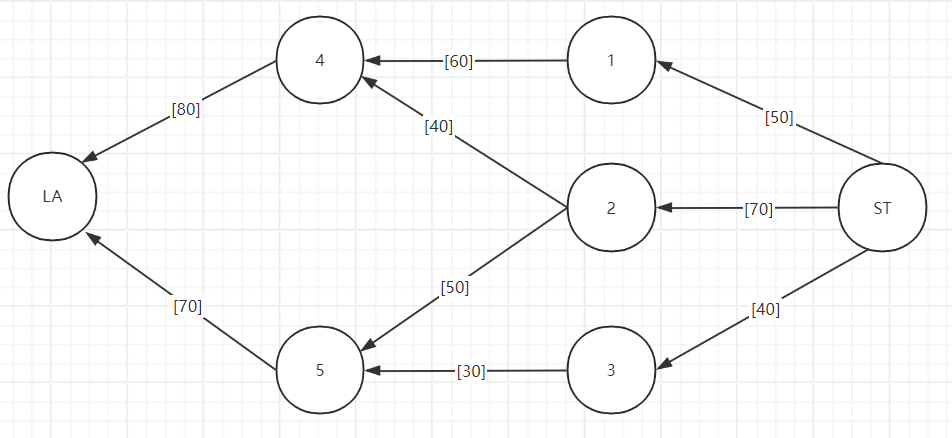
 2、目标函数：max流量=选定道路*流量；

3、约束条件：

1）每条弧的流量≤容量；

2）

a 中间点的净流量 = 0，也就是 进流量 = 出流量；

b 由于是尽力而为的供应，所以ST和LA的供应量和需求量，就不能有约束关系，就空着；

3）列表，规划求解：

 

 【最短路问题（目标是找最快、最短路径，供需至少有一方无明确要求，此时供需用1/-1表示）】

【例1】寻找网络中最短路。比如，最短的时间，最小的距离等。一个小镇的消防队，需要为附近的社区服务，从消防站到社区有很多路线。

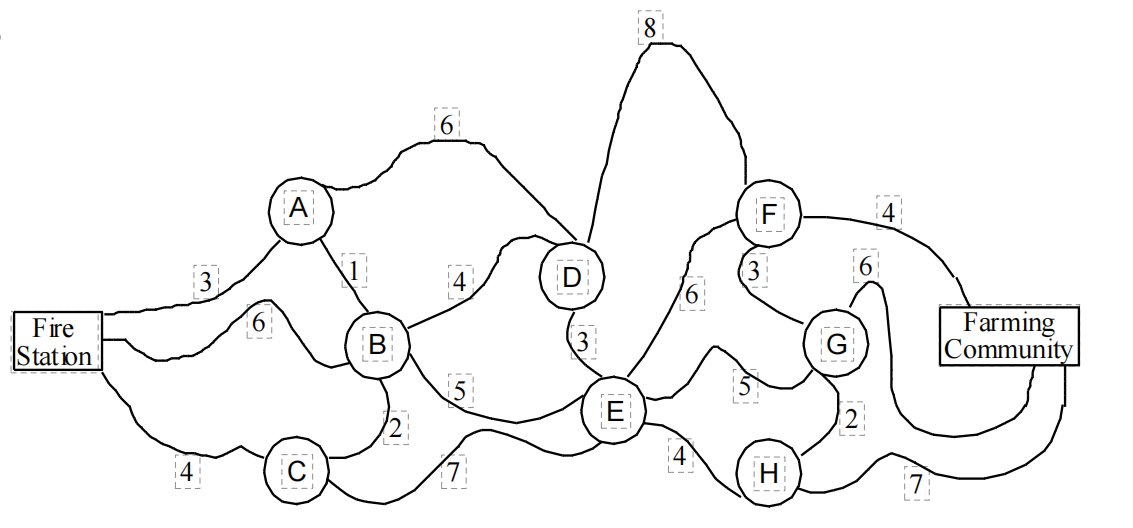
 问题：怎么走是最短路径？

【解答】

1、构建网络图：

1）节点：源、目的、中转站；

2）弧：距离。

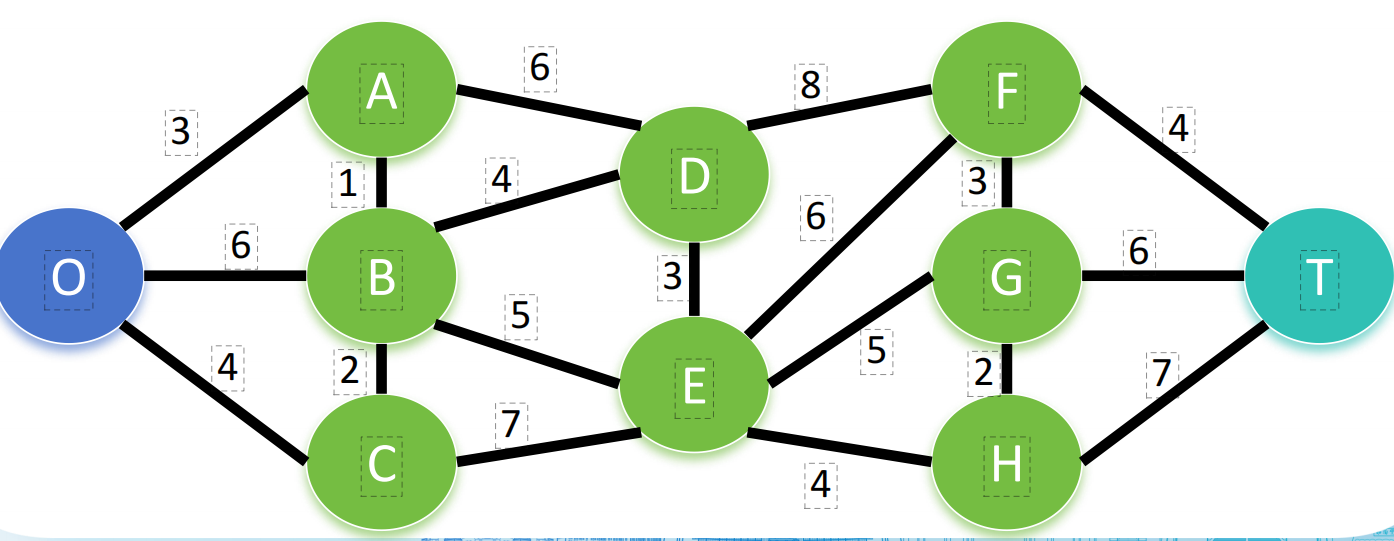
2、目标函数：min距离=选中路段（0或1，选中为1）*对应距离；

3、约束函数：

1）每个节点的流量 = 供应/需求，在最短路径的选择里，开始、结束用1和-1即可，因为不涉及真实供需；

2）选中路径只有1和0，但不需要选择为bin，因为供需决定了on route没有其他值可以出现。

4、列表，规划求解：

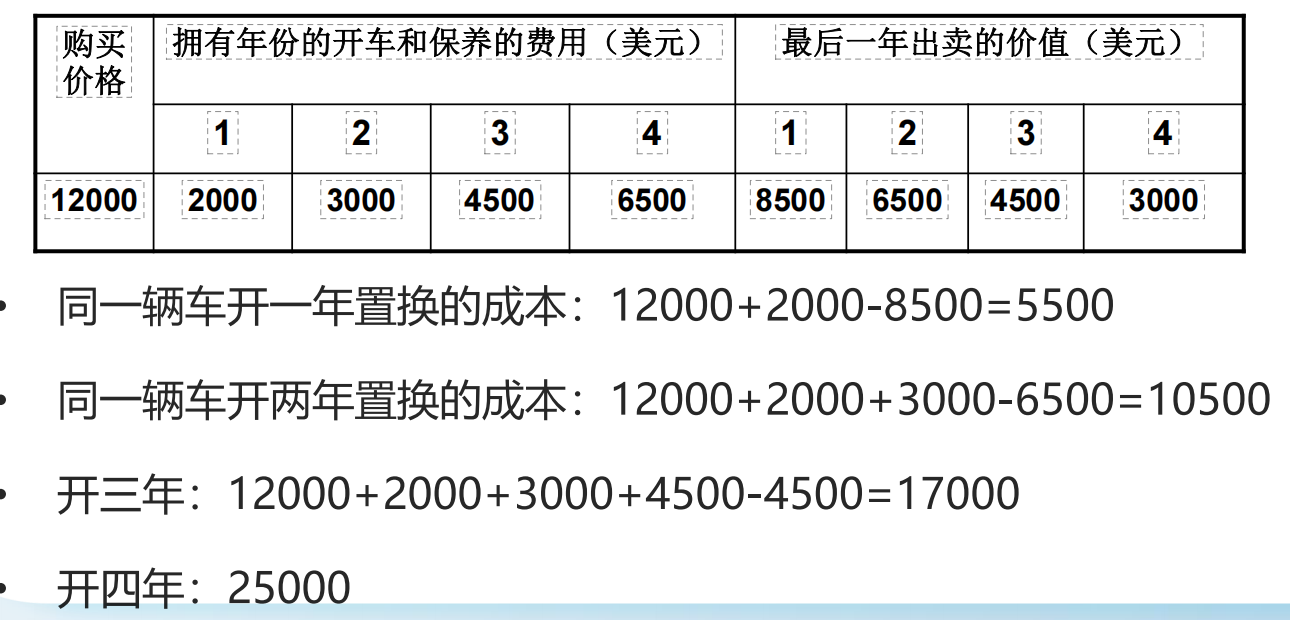
 【例2】sara父母给了她21000元，用于在大学期间买二手车，以及必要的使用、保养。购买二手车价格为12000元。使用和保养费用，根据使用年限价格不同。大学期间，她每年都可以置换新的二手车。大学4年结束后，她会卖掉车。

问题：怎么制定方案，可以使得成本最小？

【解答】

1、构建网络图：

1）节点：起始年份、中间的年份、结束的年份，所以是1,2,3,4；

2）弧：每条弧就是它这条路径的成本，所以需要先自己计算一下，第一年买了，第二年就卖了，是什么成本，这也就是节点1到节点2的弧权重，依此类推；

 

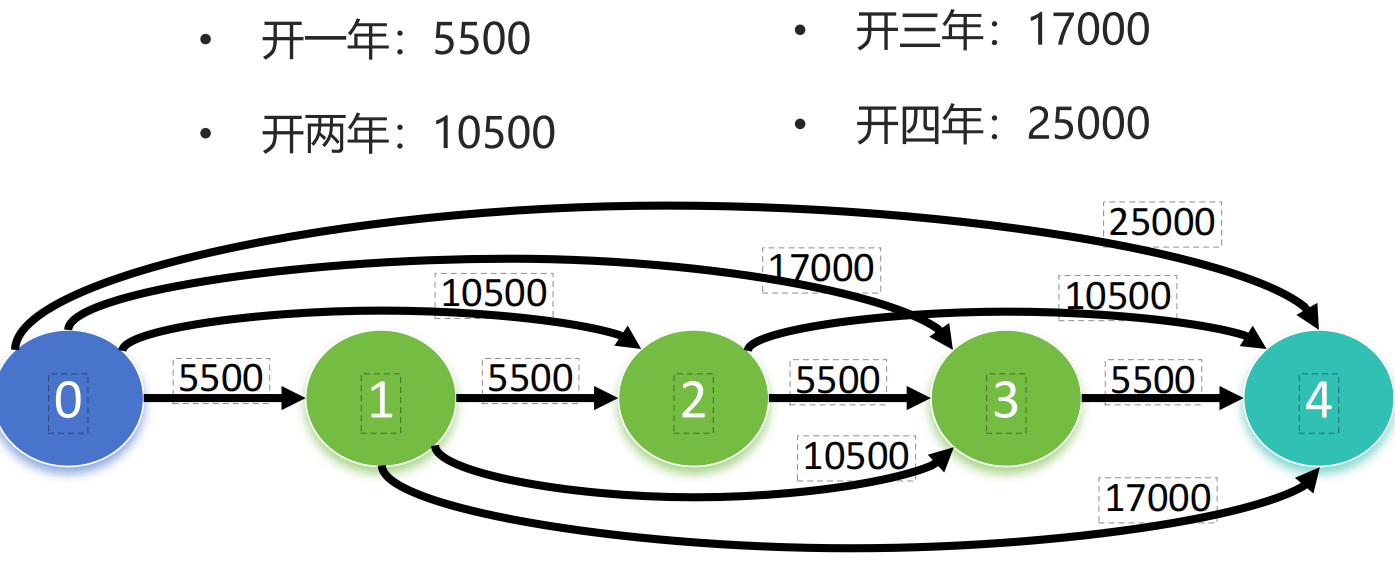
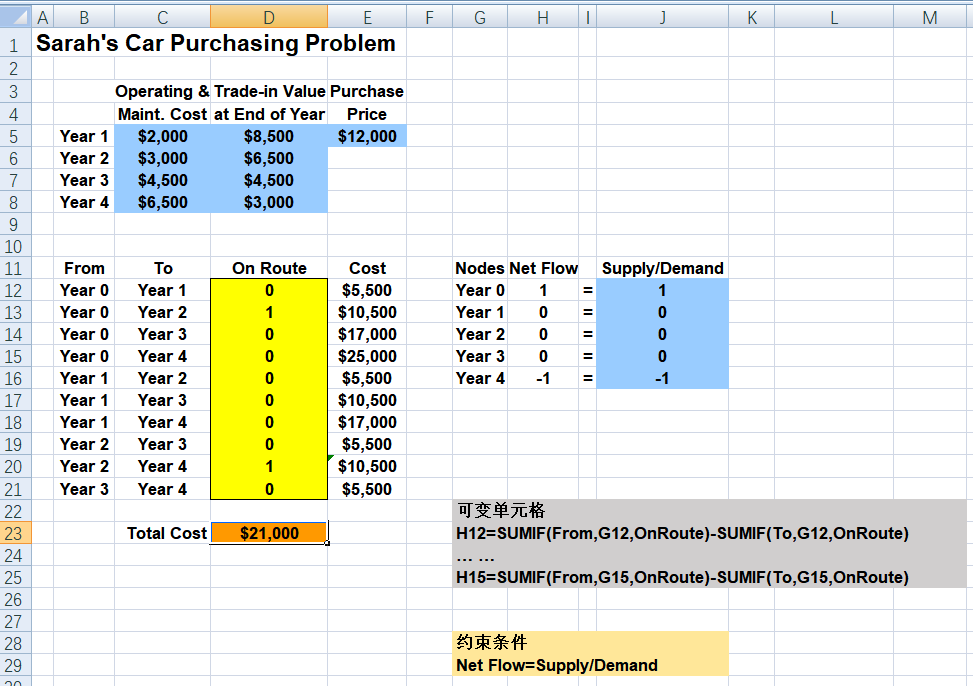
 2、目标函数：min成本=选中的路*对应的成本；

3、约束条件：

1）节点的净流量=供/需：

a 源的净流量=供=1；

b 中间的净流量=0；

c 汇的净流量=需=-1.

2）每个弧的流量小于等于容量，也就是这段弧的成本；

4、列表，规划求解：

 【例3】时间最小决策

A公司计划研制一种产品，20个月后，投放市场。整个过程分为研究、研制、设计、生产和分销。每个过程，都可以分为正常水平、优先水平、应急水平，这样可以得到不同的完成时间，当然代价是，要付出更多的成本。

问题：当前一共有3000w元，每个过程怎么决策用哪个水平，在这3000w的预算里，可以最小时间完成呢？

【解题】

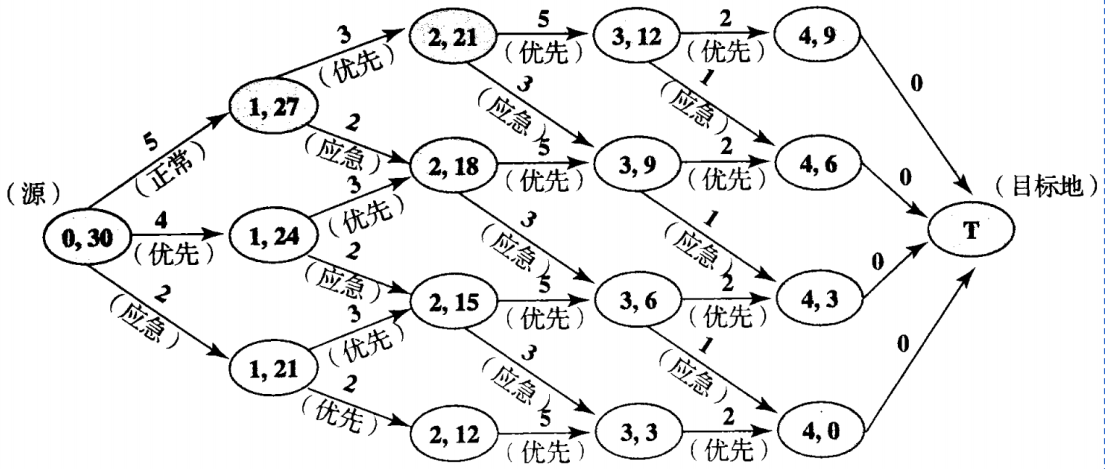
1、构建网络图：

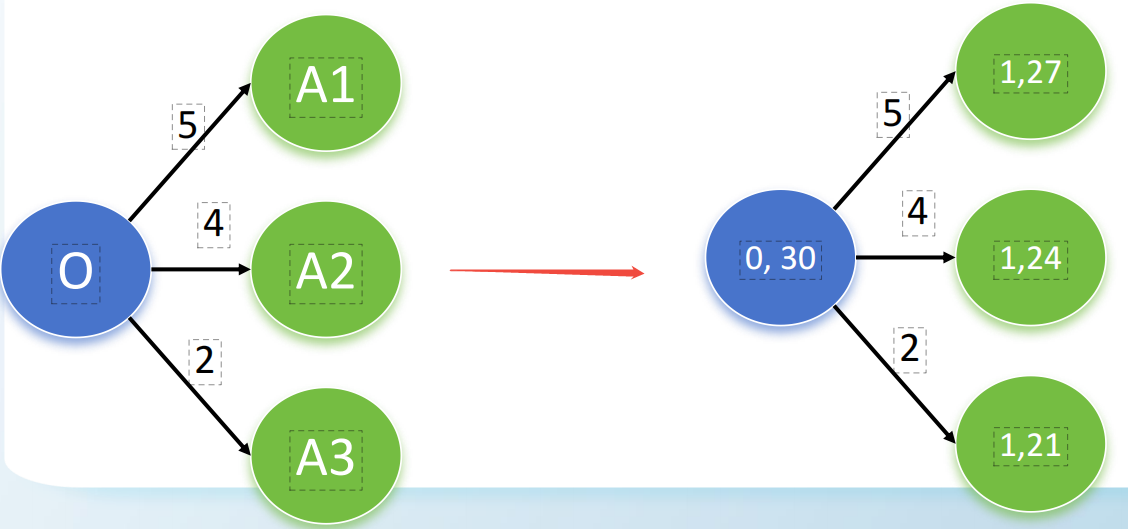
1）节点：源为开始节点，转运点为每个过程，汇为结束节点。这里注意因为每个过程有三个水平，所以需要分成3个，比如A.1,A.2,A.3；

2）弧：弧就是时间。

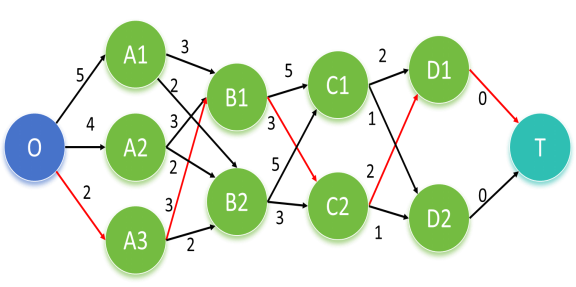
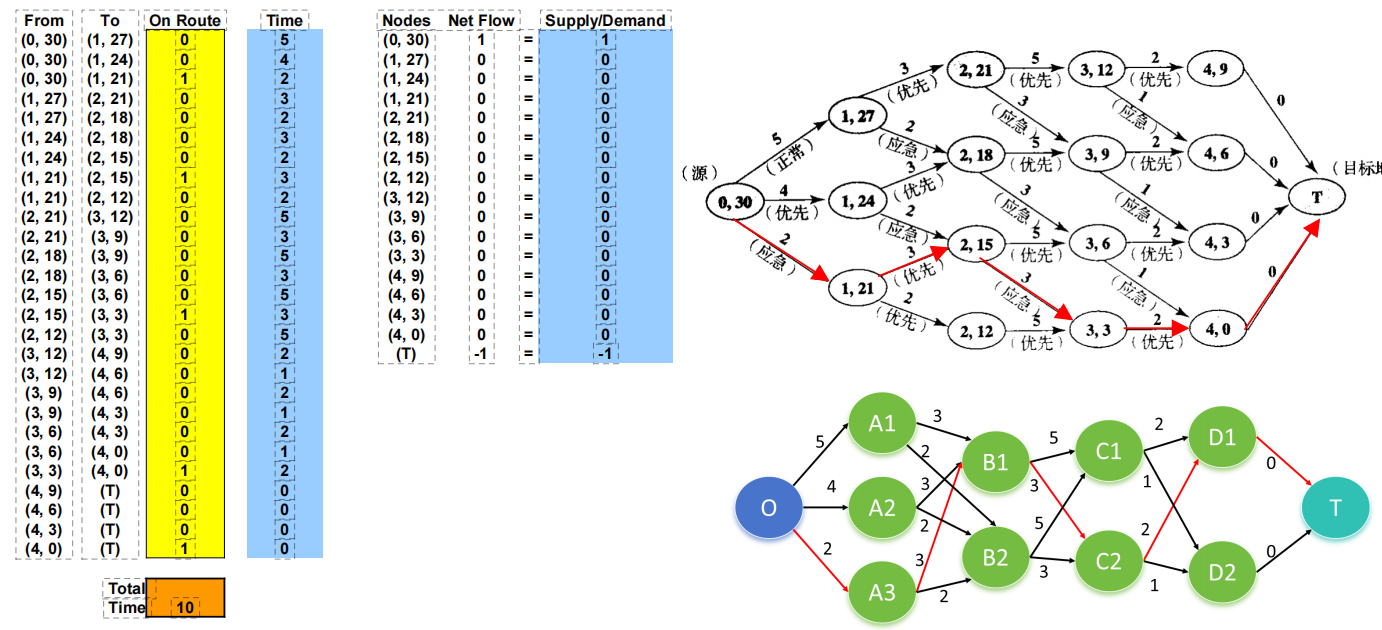
 2、目标函数：min时间=选中路径*对应时间；

3、约束条件：

1）节点净流量=供/需；

2）总成本≤30；

4、列表，规划求解：

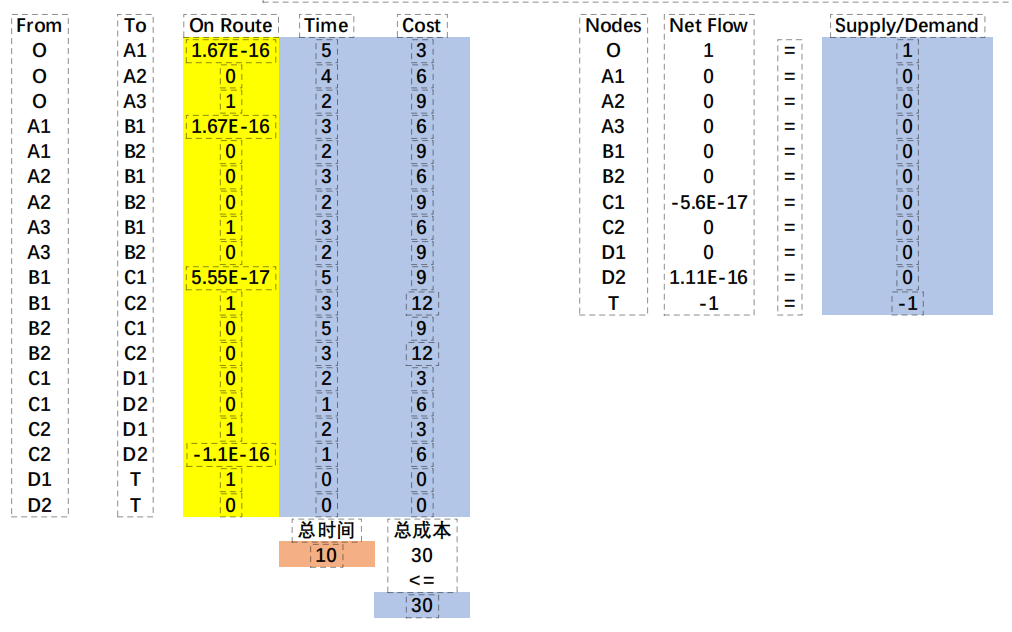
 思考：还有一种思路，是直接把成本添加到节点中计算，每个节点带着剩余成本，但这种方式我觉得稍微有点容易粗心出错，仅作为另一个思路，记录在这里：

 

 

拓展：最短路问题，数据的表现方法通常由长度矩阵（如上），还有邻接矩阵（如下）：

8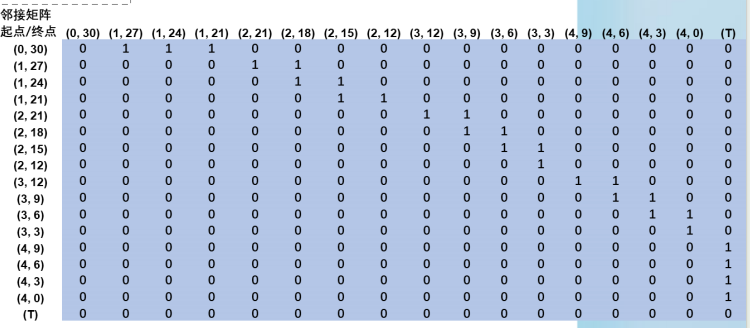

 针对更大规模的计算算法，通常有Dijkstra算法（Dijkstra算法是“贪心”策略：每次从未访问的节点中，选出当前距离起点最近的一个，然后用它去更新其它节点的距离。比如从A出发，有B和C可以选择，但是B的权重更小，就选B，然后再看从B出发，D,E的权重谁更小，就选谁，直到走到终点。）、双向搜索、A*算法（把源和汇放入一个网格内，使用曼哈顿距离方式，从起点开始，把所有路径都尝试一下，看 下一步走哪个点的曼哈顿距离+走到该点的累计成本 最小，就选哪个点，逐步走到终点。）。

关于dijkstra和A*的区别，可以简单理解为，dijkstra并不知道终点在哪儿，它只是先走好眼前的每一步，找以自己为起点，代价最小的。而A*则是有着明确的目标后，利用启发函数（就是算每个点的曼哈顿距离），找以自己为起点取走，且离终点更近的点，作为下一个点，逐步逼近目标。具体可以看下图，比如都从S出发，dijkstra会走到一个点，就尝试一下周围所有点的距离，而A*不会继续向上搜索，它会坚定地朝着目标的方向去尝试。所以实际上A*会更快。

• Dijkstra：像"水波扩散"——从起点开始，均匀地向所有方向探索，直到碰到终点。只根据 g(n)（已走距离）选择；

          

• A*：像"有目标的探路者"——它会优先朝着终点的方向探索，但不是盲目直线冲过去。根据f(n)=g(n)+h(n)（已走距离 + 预估剩余距离）选择。

      

  【最小支撑树问题】

 1、树：各个节点都是连通的，且没有圈；

 2、支撑树：一个网络里，可以覆盖所有需要的节点；

3、最小支撑树：成本最小的支撑树。

计算最小支撑树的方法，通常有两种：

1、丢边法（破圈法）：从完整的图里面（n个节点），每次选定一个圈，去掉它最贵的边，直到不再存在一个圈，得到一棵树，它会有n-1条边；

2、加边法（避圈法）：n个节点，从无边状态开始，在不成圈的前提下，一条条增加边，每次都是选择最便宜的边，直到得到一颗树（连通、无圈），它会有n-1条边。