运输与指派问题（笔记）

 

物流中，一直有一个普遍问题，就是如何用最小成本，把货物从一系列起始地，运送到一系列目的地。这个成本，有运输费，也有仓库的使用费。建模的时候，这类涉及多起始地，多目的地的，通常有3个特点：

1、决策变量一定涉及双下标（i为起始地，j为目的地）；

2、实际运送量=仓库量，实际收到量=需求量；

3、供=求

1）如果供>求，比如仓库库存多了，这时候实际送到的量应≤仓库量；

2）如果供<求，比如需求量变大了，这时候实际收到的量应≤需求量。这里注意，供不够了，不管是人力不足，还是物力不足，那么所求一定会存在不足，不会默认可以通过“加班”这些方式，来保证供=求的情况；

4、如果某条链路损坏了，则直接把这条路线的成本，设置为一个很大的数值即可，这样计算成本的时候，就不会使用这条线路。或者决策条件里，直接在约束条件设置时，手动将某条线路的实际使用量设置为0。

 

【示例1】某飞机制造公司，最后一步是生产发动机，安装到飞机的机框上。问题，每月生产多少发动机，使得制造和存储成本最小？

 

 【解答】

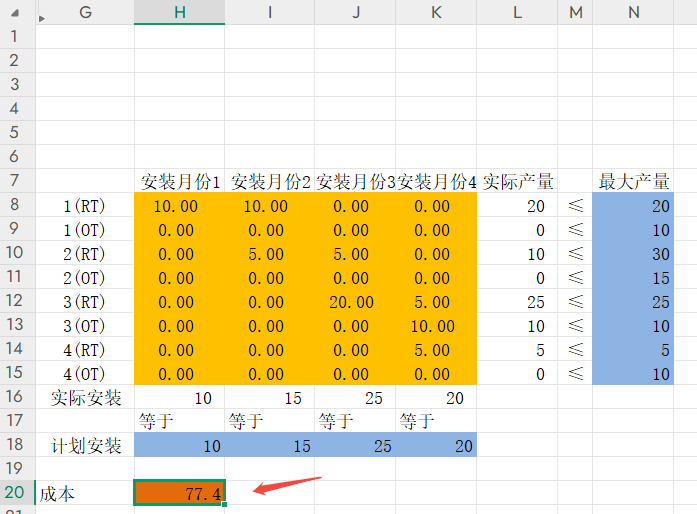
1、规范化数据。根据表格中的数据，整理合适的数据模型。比如需要区分月份、正常时间、加班时间，以及，哪个月份生产的，会涉及哪些月份的存储成本。解释：对于1（RT），就是1月份正常加班，可以在1,2,3,4都安装，所以1月份就安装，就不涉及存储，成本就是B8=B2，如果2月份安装，需要有1个月的存储费用，就是C8=B2+E2，如果3月安装，需要2个月的存储费，就是D8=B2+2*E2。依此类推；

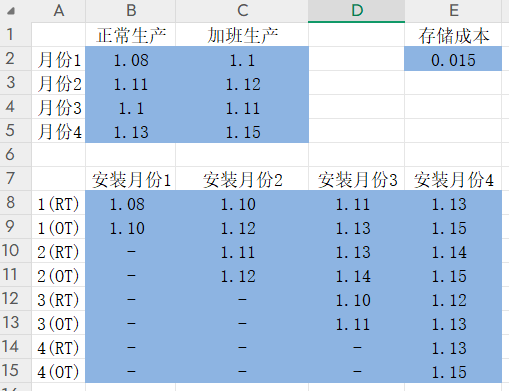
 2、目标函数，即每个月的安装的总费用，也就是加工成本+存储成本，对应相乘每个月的安装数目；

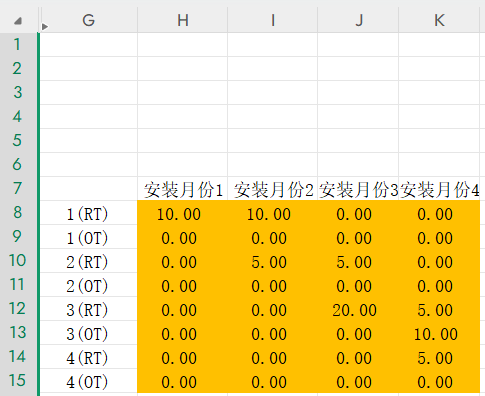
3、约束条件。：

1）每个月都有计划安装的数目。所以每个月实际安装 = 计划安装；

2）每个月不同工作方式，都有最大的产量。所以每月不同工作方式总量≤最大产量；

3）2月份生产的，1月份不会安装，因此，2月份生产的，对应1月份的RT,OT都要手动置为0，3月份生产的，1,2要置为0,4月份生产的，1,2,3要置为0；

4）所有数值非负；

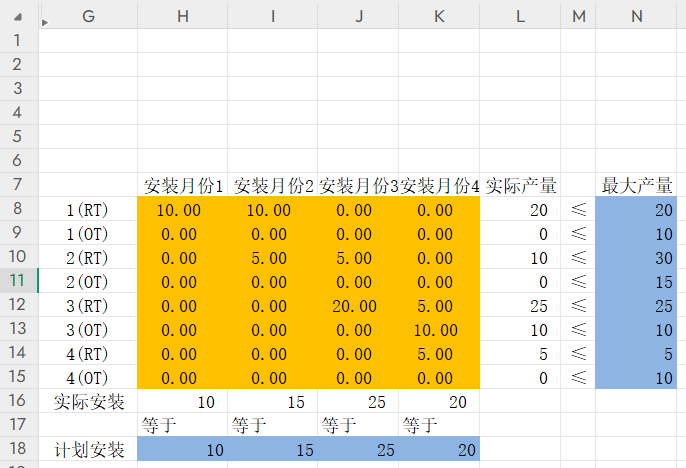
 4、规划最优解：

 

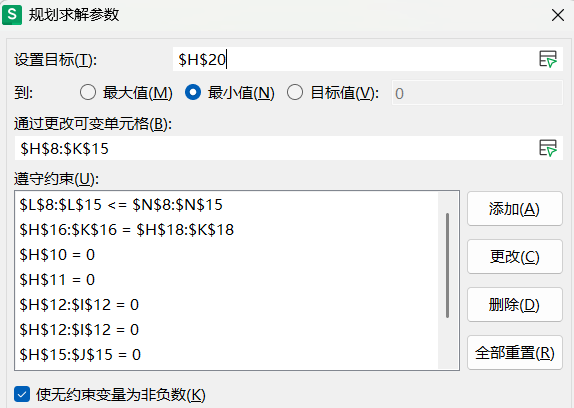
 结果：

 

【示例2】要给一家公司的4名职员安排工作，每个人处理不同工作的时间数据和每小时工资情况如下（不单独贴了，直接参考蓝色整理后的数据），请问怎么分配工作，可能花费最小的成本？

【解答】

1、整理原始数据：

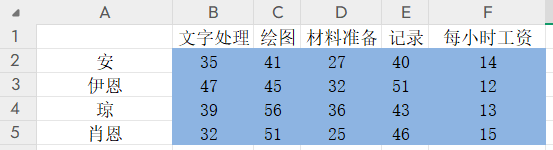
2、目标函数。最小成本=每个人最终获得的工作*对应工作花费的时间*工资。

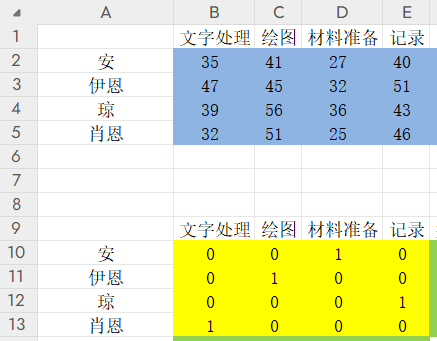
为了计算方便，可以把“每个人最终获得的工作*对应工作花费的时间”，单独列出来，他们分别等于=SUMPRODUCT(B2:E2,B10:E10)，依次类推：

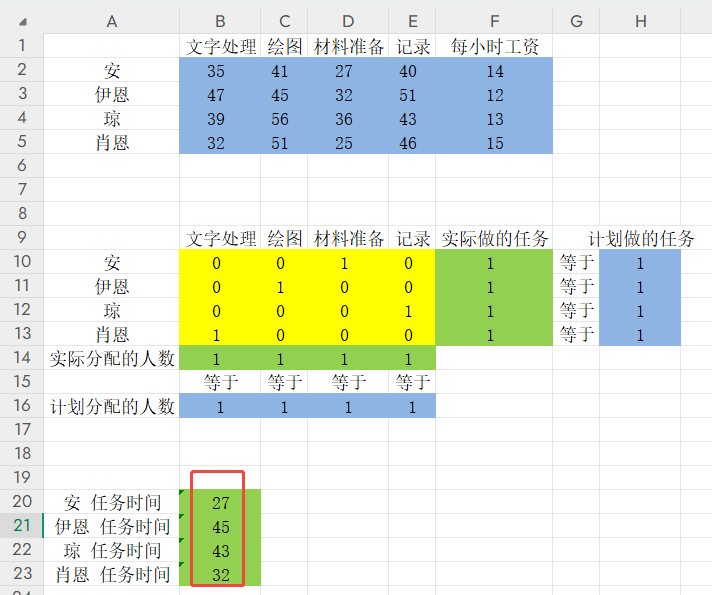
  3、约束函数。每个人干一个，每个工作都得有人干：

1）每人实际做的任务量=计划做的任务量（也就是1）；

2）每项任务实际分配的人=计划分配的人（也就是1）；

3）全部非负；

4、规划求解：

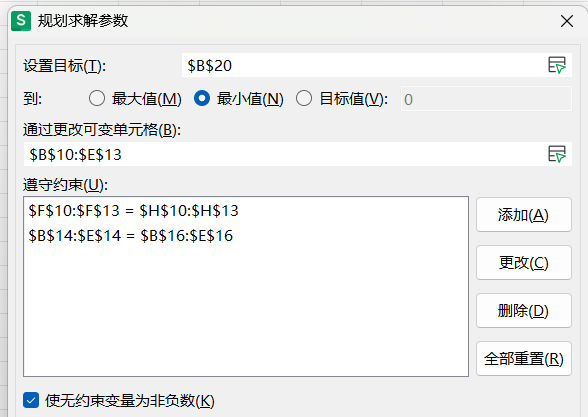
 结果：

 

 【示例3】上题做一个变种。其中，琼无法完成绘图工作。规划求解有两种思路：1）让琼做这项工作的时间成本，直接写到最大，比如900，远大于大家的平均工作时间，如下图；2）手动将琼决策变量（黄色）中绘图这个值，在约束条件中，置为0。

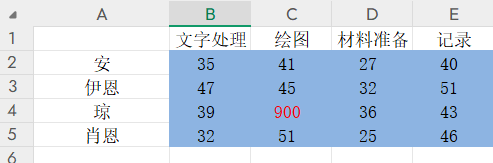
 其余计算思路和上题一致，不再赘述，结果如下。由于琼本来就不会被分配这项工作，所以成本无变化：

 

 

在运输规划类问题中，还有一类特别的，就是整数规划，它有几个特点：

1）线性规划，但有整数约束；

2）涉及特定某些值，或者限定某些值的问题。比如N选1或N选2、选了你，就得选我、最多或者最少选几个；

3）整数规划，无法进行敏感性分析。

 

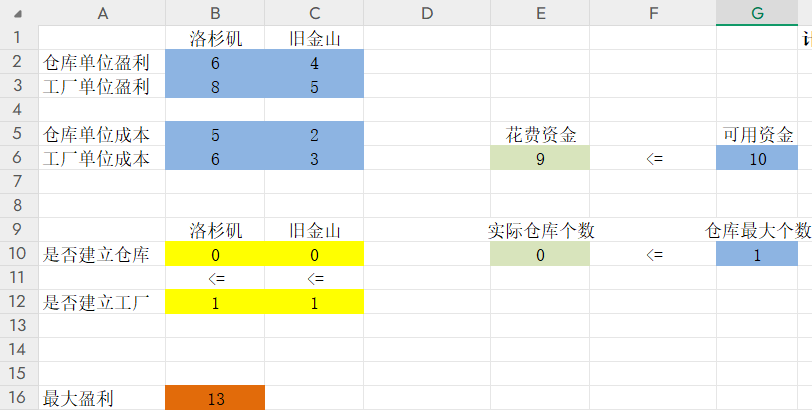
【示例1】在洛杉矶和旧金山建立工厂和仓库的盈利、成本如下。总可用资金为10，两地可建立的仓库个数，最大为1。每个地方只有建立工厂，才有可能建立仓库。请问要保证盈利最大，两地是否需要建立工厂和仓库？

 

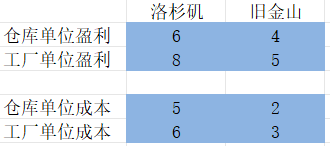
  【解答】

1、目标函数：最大盈利=盈利-成本，也就是sumproduct(个数，盈利)-sumproduct(个数，成本)。所以要想盈利最大，盈利固定的情况下，成本就要最小；

2、约束条件：

1）每地仓库个数≤每地工厂个数；

2）总花费（即sumproduct(个数，成本)）≤10；

3）仓库个数（即sum(两地仓库个数)）≤1；

4）是否建立仓库、是否建立工厂，均为二进制；

5）所有数据非负；

3、规划求解：

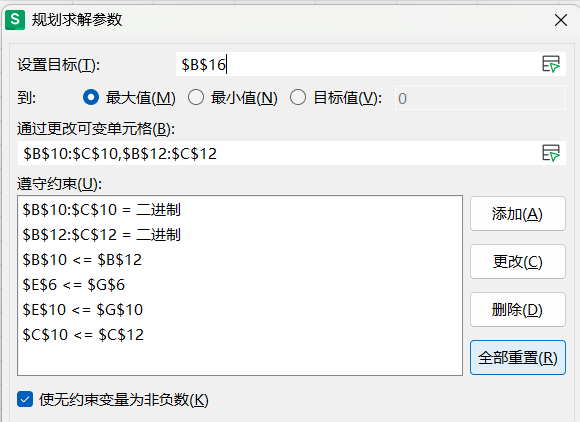
  答案

 

 

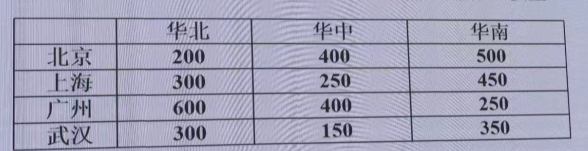
【示例2】某公司考虑在北京、上海、广州、武汉建立库房，负责华北、华中、华南三个地区的发运，每个库房每个月可以处理1000件货物。在北京设立库房，成本是4.5w，上海是5w，广州是7w，武汉是4w。每个地区的月平均需求量为：华北600件，华中700件，华南800件。发货的费用见下表。公司希望在满足地区需要的前提下，是平均月成本最小。且满足三个条件：1）如果在上海设立库房，则武汉也必须设立库房；2）最多设立3个库房；3）武汉、广州不能同时设立库房。建立一个模型，并计算。

 【解答】

1、目标函数：最小成本=发货（即sumproduct（各地发货的钱*各地发货件数））+库房；

2、约束函数：

1）北京、上海、广州、武汉是否建立库房的值，为二进制；

2）上海是否建立库房的值≤武汉是否建立库房的值；

3）所有是否建立库房的值 总和 ≤3；

4）武汉是否建立库房的值+广州是否建立库房的值 ≤1；

5）每地每月供货量的公式，需要和是否建立仓库有关。即：sumproduct(每地发给不同区域的发货量*每地发给不同区域的费用)+1000（1-该地是否建立仓库），也就是只有建立仓库，这个地方才涉及是否小于可供货量的比较。注意，这个值只能写1000，如果写10000，那已经不符合≤1000的要求了，写999之类的，由于不建立仓库计算为999+sumproduct，没有达到最大值1000，这样是否设立就有可能为小数。具体以北京为例：

如果北京建立仓库，就是1，那么每月北京供货量就是：sumproduct(（200,400,500）相乘相加（北京发给华北、华中、华南的发货量）+1000（1-1）=sumproduct(（200,400,500）相乘相加（北京发给华北、华中、华南的发货量）；

如果北京不建立就是sumproduct(（200,400,500）相乘相加（北京发给华北、华中、华南的发货量）+1000。因为我们在计算最小成本，这样一来这一项成本就很大了，一定不要了 ；

6）每地区每月发货量等于每地区每月需求量；

3、规划求解：

 

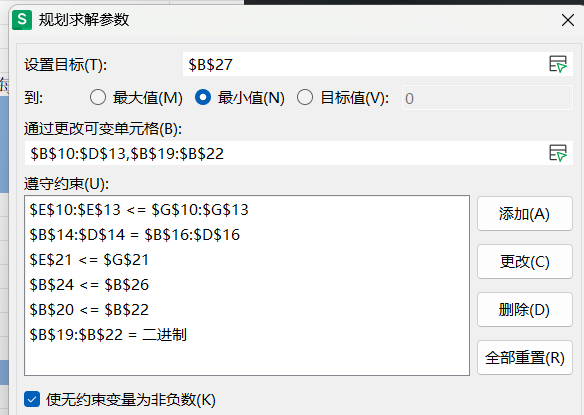
答案