敏感性分析（笔记）

 

什么是敏感性分析？

数学模型只是实际问题的一个粗略的抽象，最优解也只是针对某一特定的数学模型。管理者要对未来做各种假设，在这些假设下，测试可能产生的结果，通过对各种结果深入分析来指导决策。通常，在取得最初版本模型的最优解之后，进行分析才能取得对问题深入的认识，这种分析称为 what-if分析，或 敏感性分析（Sensitivity Analysis）。

 

比如，线性规划中，一开始的例子，选择最优数目的大积木和小积木，制作出椅子和桌子，并获得最大利润。如果此时，单台桌子的利润提高了，那之前的最优数目，还是最优么？如果又增加了一个大积木，这时，总利润，会增加么？怎么分析这样的问题，是科学、合理的，这就是敏感性分析的意义。

 

使用solver table自动规划求解 

当我想调整目标函数系数，或者R.H.Side（约束条件右边的值，也就是可用资源等），然后观察对最优解的影响，看最优解的变化。当然可以手动修改表格，重新点击“规划求解”来得到答案。但是如果我想看一定规律的变化，然后得到每个系数变化后，最优解的变化，手动一个个生成最优解就太麻烦了，而且还需要手动整理数据。这时候，就可以使用solver table帮我们自动根据系数的变化，生成最优解的表格。

 

例1 使用solver table自动计算最优解（仅变化1个数据，看对最优解和目标函数的影响）

某公司生产门窗，单位获利，生产时间的数据如下，计算出门窗的最优组合为2门6窗，此时，可获得最大利润3600元。那么门单位利润的变化，会对最优解和最大利润有怎样的影响呢？

首先，先尝试通过手动修改，并生成最优解来观察、理解一下这个变化：

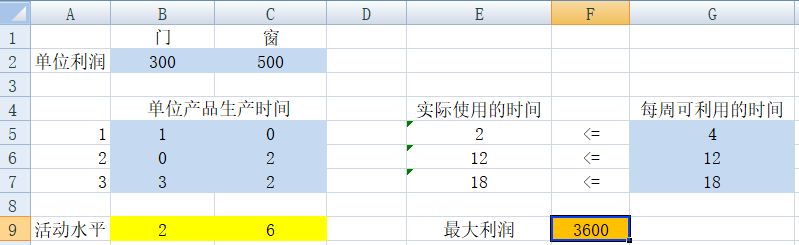
当门的单位利润降到200，那么最优解和最大利润是否变化呢？通过直接修改表格数据，得到如下结果，最优解不变，还是2门6窗，但是最大利润会降低到3400元。

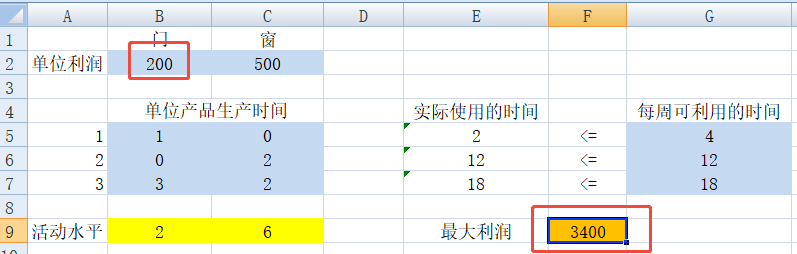
继续调整，门的单位利润升高到500，那么最优解和最大利润是否变化呢？通过直接修改表格数据，得到如下结果，最优解不变，还是2门6窗，但是最大利润会升高到4000元。

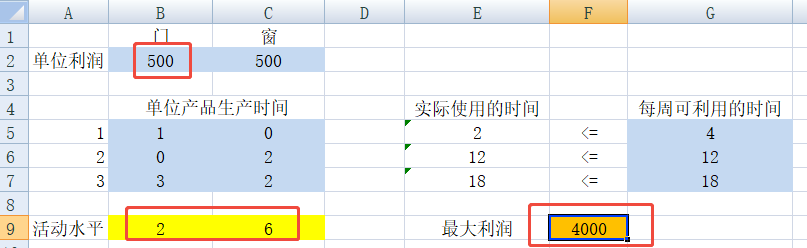
 如果，门的单位利润升高到1000，那么最优解和最大利润是否变化呢？通过直接修改表格数据，得到如下结果，最优解变化为4门3窗，最大利润会升高到5500元。

 

现在，通过使用solver table，可以自动得到一个变化的规律表格：

1）建立一个表格，第一行数据，把需要solver table帮你计算的数值，都配好等式模型。如，你要计算门窗数目和利润变化，C13=B9,D13=C9,E13=F9； 

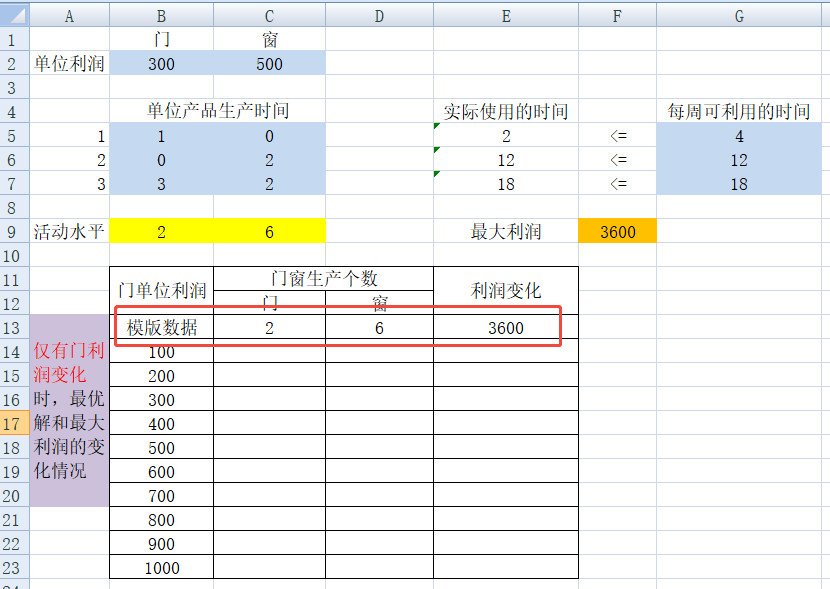
  2）选中要生成的目标区域，点击“加载项-solver table”，列那里，选中B2，点确定。自动规划求解，每种门利润的情况下，最优解和最大利润的变化情况。可以看到门单价没有超过800时，最优解不变，利润有变化，超过800，最优解开始变化。

 

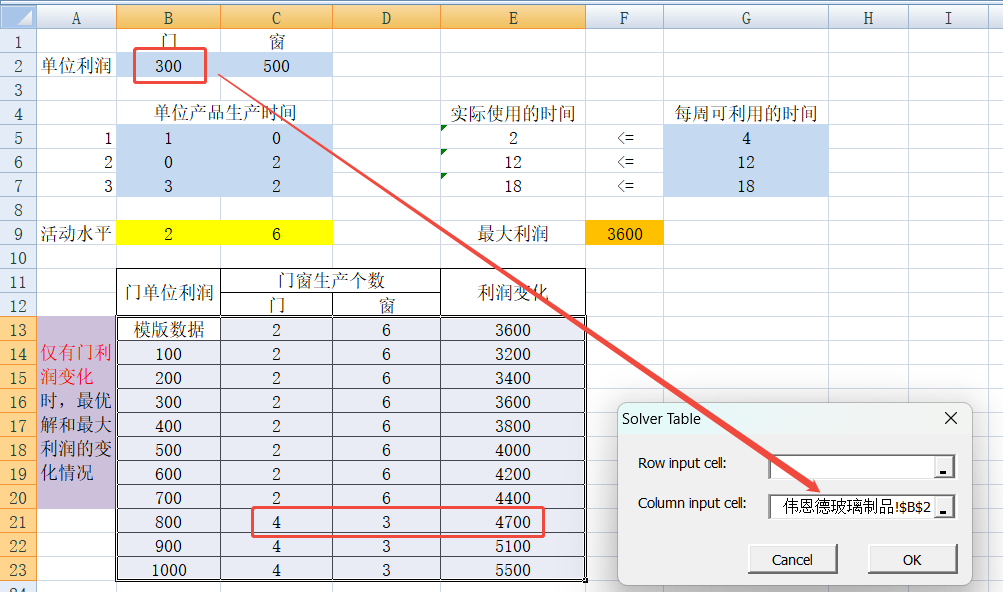
例2 使用solver table自动计算最优解（变化2个数据，看对目标函数的影响）

配置时注意，横排写窗的变化100->500，列写门的变化300->500，左上角要配置一次你需要帮你计算的数值，也就是总利润 C27=F9，就是3600。然后solver table 的row选窗单位利润的单元格，column选门单位利润的单元格，点ok即可。所有对应组合的利润，会生成在交叉的格子中。比如100窗+300门=1500利润。

 结果为：

 例3 使用solver table自动计算最优解（变化2个数据，看对最优解的影响）

这个题和上个题的区别在于，我需要在二维表格中，求解一个组合解，即包含门、窗两个结果的解。

首先，规划求解，在选项配置时，精度要调整为0.1，不要太小，否则小数点太多；

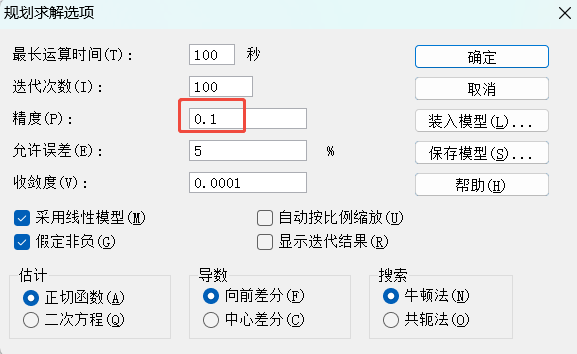
然后，配置上和上面不同的地方是，模版数据不能简单地输入“=F9”，我们想得到的是一组表格的结果，比如门窗数量组合为（2,6），这对应的是B9和C9。写法上应为：="("&B9&","&C9&")"

 答案为：

 

怎么查看敏感性分析报告

 1、敏感性分析报告--递减成本、目标函数系数部分

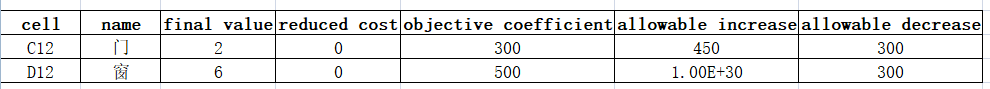
 以上是我们获得的一份，关于上述门窗情况的敏感性分析报告，包含递减成本和目标函数系数的部分，解读如下：

1）每行解读了门窗相关变化值，final value是最优解，最后三列是 当前门窗的单位利润（目标函数的系数）、目标函数系数可增加的最大区间、目标函数系数可减少的最大区间，即300-300（0）--300+450（750），在这个范围内变化，不会影响最优解；

2）敏感性分析报告，可以在无需重新求解的情况下，判断模型参数的变化，是否造成了最优解的改变。当数据庞大时，这会有很大的帮助；

3）reduced cost，一个东西，如果想获得利润，需要增加/删减的量。这个题里面都是0，代表门窗已经都是最优，没有必要再增减了。并且给出一个范围，在这个范围里，增加门窗，reduced都不会变化。假如窗的当前个数是0，reduced是-50，意味着，它至少要增加50的利润，或者降低50的成本，它才有生产的必要；

4）使用百分百法则，可判断，当多个系数变化时，最优解的变化。如果计算为≤1，则最优解不变，如＞1，则最优解会变化。如下：

 4.1）门、窗利润如果分别变成450和400，则450-300/450 + 500-400/300 < 1。根据百分百法则，最优解不变；

 4.2）门、窗利润如果分别变成600和300，则 600-300/450 + 500-300/300 > 1。根据百分百法则，最优解会变化。

注意：

1、百分百法则就是要判定，多个系数变化，是否会引起总体最优解的变化，上面第二种情况就证明了，即使单独都在最优区间，也会影响最优解；

2、百分百法则是一种变化可能的推断。上述第二种情况，其实作图会看到，在（2,6）这个点依然会达到最优解，并没有变。

 

 2、敏感性分析报告--影子价格部分

影子价格，简单描述就是，某个约束条件变化了，利润或成本会上升多少或者下降多少，这个差值，就是影子价格。

1）如果，影子价格为0，代表，当前约束条件，小于终值，这时候你只要在允许的范围内增加/减少约束值大小，都不会对利润/成本有影响，也就是，影子价格有效（虽然这个价格，就是0）。如果超过了，那么就不是这个影子价格了，也就是，影子价格无效；

2）如果，影子价格不为0，代表，当前约束条件，已经就是终值了，你增加/减少约束条件，都会影响利润/成本，影响的值就是影子价格。并且，这是在允许的范围内，增加/减少约束值，才是这个影子价格，也就是，影子价格有效。超过了这个允许范围，那就不是这个价格了，也就是，影子价格无效了。

这一部分的敏感性分析中，主要看影子价格。解读如下：

1）Final value是最终计算的工时结果，shadow price是调整约束条件后，对总目标函数的影响，constraint R.H.Side就是右边的约束条件，也就是可用工时，最后两列就是允许增加和减少的区间；

2）当约束条件在allowable区间变化时，最优的目标函数值会增加/减少多少。如果影子价格是正的，就表明右边约束条件的增加，会增加目标函数的值；如果影子价格是负的，就表明右边的增加，会降低目标函数的值。如果影子价格是0，代表当前某个条件远没达到上限，约束条件继续增加也不会影响影子价格，但通常下限是会有要求的，为当前约束值-终值，也就是这是buff区间。比如这个表格中，工厂2使用的工时，当从12增加1，到13时，最大利润会增加150，如果从12减少1，到11时，会降低150。如果这个150本来就是负数，比如-150，那么12增加1小时，利润会降低150，就是和正数反着来。工厂1的终值是2，但约束条件是4，代表约束条件最多可以再下降4-2这个buff，然后影子价格就会失效了，就是不再是0，而是对利润，成本有影响了。上限是无穷，是因为2本来就小于4，这时候把4继续调高，自然不会影响工厂1的利润，成本。

 

这和我们通过solver table观察到的计算结果一样，如下图。注意计算时，可通过solver table得到门窗、总利润的变化，但灰色影子价格需要手动计算，也就是利润的差值（方法：在工时5的影子价格单元格，使用公式：下面格子-上面格子，然后手动拖动到工时10为止即可）。根据结果可以看到，和敏感性分析符合；

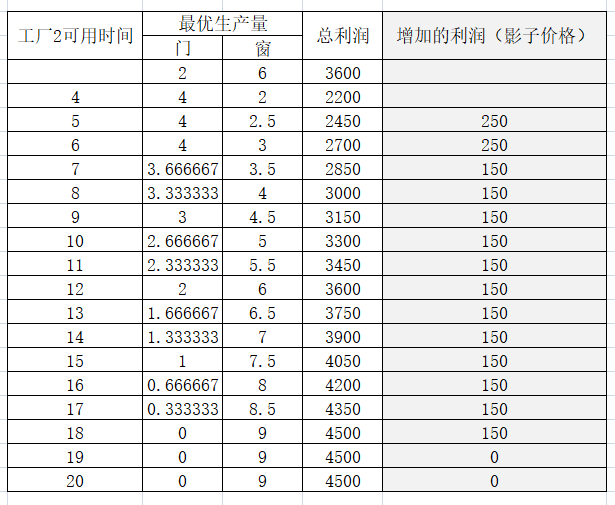
也可用用百分百法则来验证这一次约束条件的变化，影子价格是否有效。百分百法则会更灵活一些，比如同时变化两个系数，把工厂3 1个工时挪给工厂2 用，计算方式为 13-12/6 + 18-17/6 ＜ 1 ，小于1，说明这个变化下，影子价格有效。

 

 扩展：为进一步理解影子价格，继续解读下表。某公司有个排班计划，5个班，在不同时间段工作，每次工作都需要覆盖连续的4个小时，具体排班时间和敏感性分析报告如下。思考一个问题，哪个时间段，约束值在允许范围的变化，不会对成本有任何影响呢？

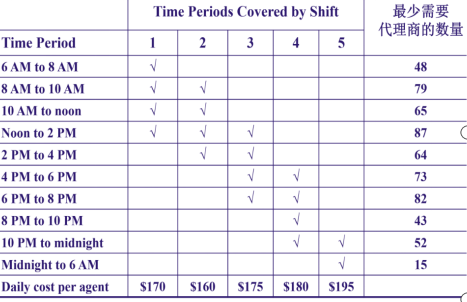
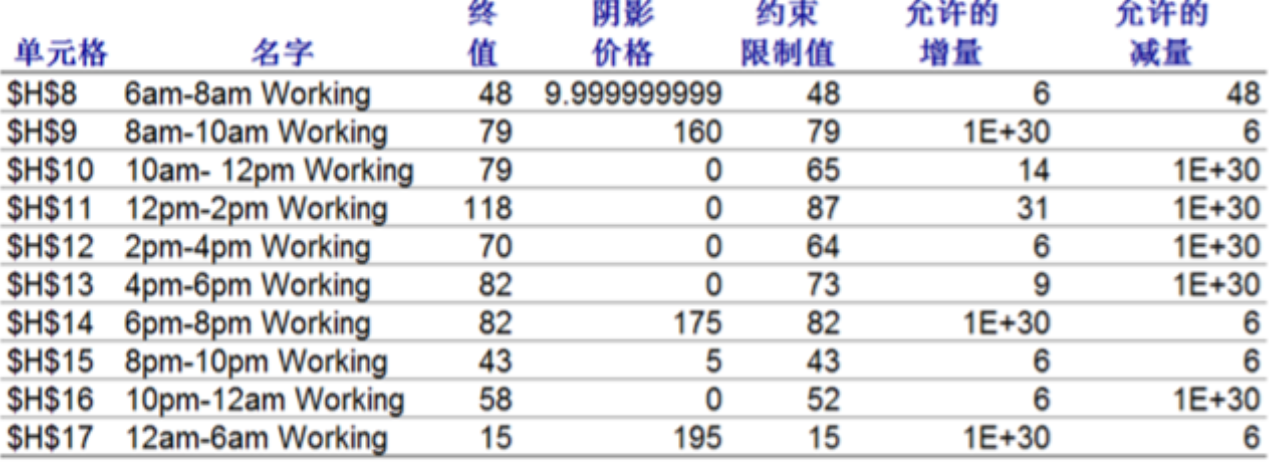
 思考的方式，就是看哪个时间段里，影子价格为0.因此就是10-12,12-2,2-4,4-6,10pm-12am。

 

整体小结：

1、what-if敏感性分析，是求得最优解以后，再进一步考虑系数变化影响、约束限制值变化影响时去使用的；

2、敏感性分析递减成本部分，是基于目标函数系数的变化，判断对最优解的影响；而影子价格部分，是判断约束条件的变化，对目标函数值的影响；

3、以下两种方法都可以计算某些参数的变化，对最优解、目标函数值的影响：

3.1）solver table可以根据系数变化，自动求得所有的最优解、目标函数具体的值。最大可以基于2种系数的变化，求得对应变化的最优解、目标函数具体的值；

3.2）百分百法则，可以根据系数变化，判断最优解、目标函数值是否会变化，但不会得到一个具体的值。可以计算N种系数的变化，对最优解、目标函数值的影响。