线性规划（二 具体应用）

 

线性规划，主要解决资源分配问题、成本收益平衡问题、网络配送问题、混合问题。

 

【资源分配问题示例】资源分配问题，目的是，使用有限的资源，获得最大的利润，约束条件是，使用的资源小于等于可用的资源。

示例1：

【问题】某公司为A产品，制定了促销活动。主要方式有三个：

1、星期六上午儿童节目的电视广告；

2、食品与家庭导向的杂志广告；

3、主要报纸星期天增刊上的广告。

有三种资源会限制做这些事：

1、广告预算（4000000元，即400w）；

2、计划预算（1000000元，即100w）；

3、可获得的电视广告时段是5个。

 

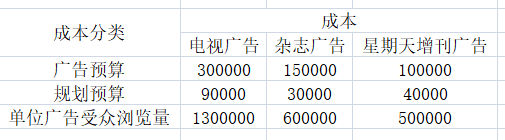
 问，怎么确定每个广告活动的使用效果，即最大的受众量，以此来制定最优的广告组合去促销。

【求解】

1、假设，电视投放了x个广告时段，杂志投放了y个广告数目，增刊投了z个广告数目。则目标函数是max（最大受众量）=max(1300x+600y+500z)；

2、约束条件：

1）300x+150y+100z≤4000；

2）90x+30y+40z≤1000；

3）x≤5；

4）x,y,z ≥0.

 3、excel 2007制作表格，求最优解：

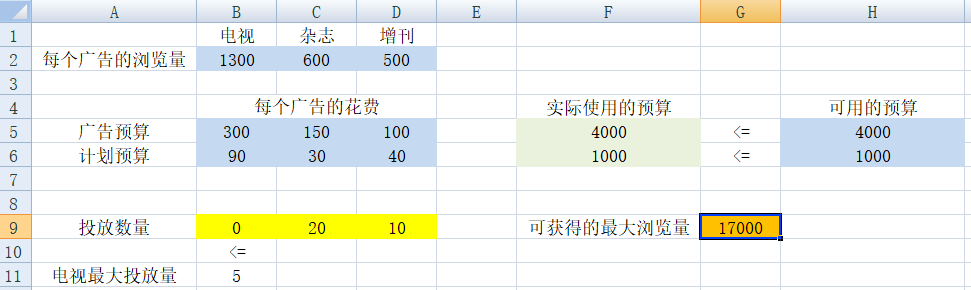
1）蓝色为原始数据，黄色为决策变量，绿色为根据决策变量获得的输出值，橙色为最终计算出的目标值：

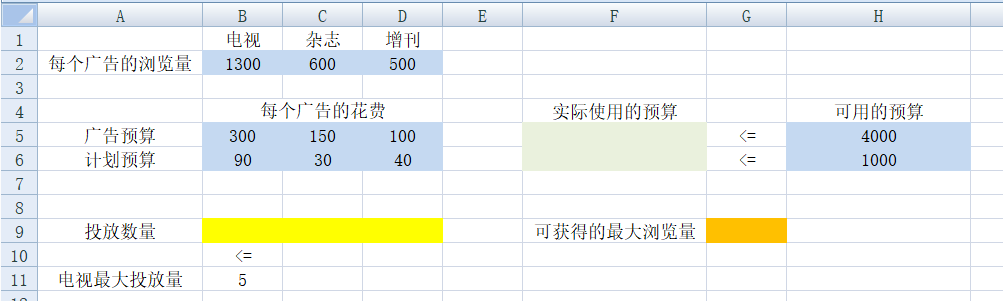
 2）设置等式模式：

• F5=SUMPRODUCT(B5:D5,$B$9:$D$9)
• F6=SUMPRODUCT(B6:D6,$B$9:$D$9)
• G9=SUMPRODUCT(B2:D2,B9:D9)

3）计算最优解：

 

 

 

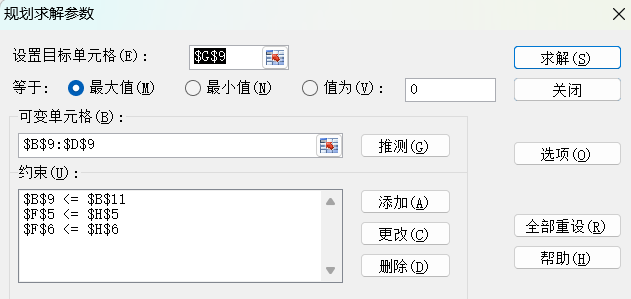
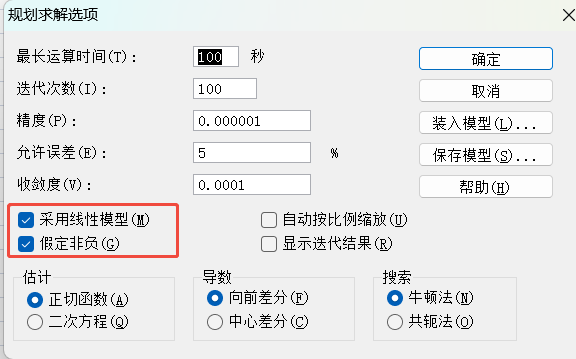
示例2：

某公司需要在四个不同的时期对三个项目投资。当前先预付定金，并在1,2,3年后，分别追加投资。主要投资这三部分：

1、高层办公楼；

2、宾馆；

3、购物中心。

每年可供投资的金额如下（注意：前一期没用完的话，就可以继续在下一期使用）：

1、现在：2500w；

2、1年后：2000w；

3、2年后：2000w；

4、3年后：1500w。

 

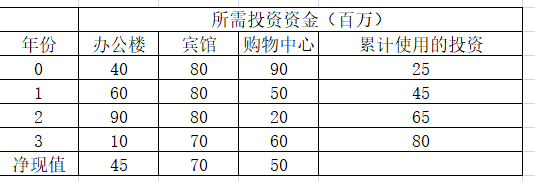
 请问，该公司在各个项目的投资占比怎么规划，才能获得最大的净现值（净现值是指一个项目预期实现的值与实施该项计划的现金支出的值的差额，简单说就是 挣的钱-投入的钱 ）？

注意：这个题目的阅读理解，有个地方要注意，就是每个项目，根据所占比例，获得了对应的资金，但是这个资金，是不够完整达到这个项目所需的所有资金。比如当前这一年的办公楼需要40百万，宾馆80百万，购物中心90百万，但这一年，我只有25百万的预算，这25百万，假设按照20%，30%，50%分别给了办公楼，宾馆，购物中心，那么每个项目的投资钱数，就是40*20%，80*30%，90*50%。当然，得到的净现值，也不会是完整的45+70+50，而是45*20%+70*30%+50*50%。我觉得这可能和课本的翻译有关系。

【求解】

1、设办公楼项目的投资比例是x，宾馆比例是y，购物中心比例是z。则目标函数为max（净现值）=max（45x+70y+50z）；

2、约束条件，这里有个地方要特别注意，就是投资的话，上一年没用完，那么下一年就可以拿来继续用，所以：

1）当前：40x+80y+90z≤25；

2）1年后：（60x+80y+90z）+（40x+80y+50z）≤ 45，即前一年+今年一共的投资不超过到这一年为止，累计可投的总投资45。这里一定要注意，这个45其实已经包含了第0年的25，所以不能计算为45+25；

3）2年后：（90x+80y+20z）+（60x+80y+90z）+（40x+80y+90z）≤ 65；

4）3年后：（10x+70y+60z）+（90x+80y+20z）+（60x+80y+90z）+（40x+80y+90z）≤ 80

以上全部化简后：

1）当前：40x+80y+90z ≤25；

2）1年后：100x+160y+140z <=45；

3）2年后：190x+240y+160z ≤ 65；

4）3年后：200x+310y+220z）≤ 80；

5）x,y,z≥0.

3、excel求最优解。

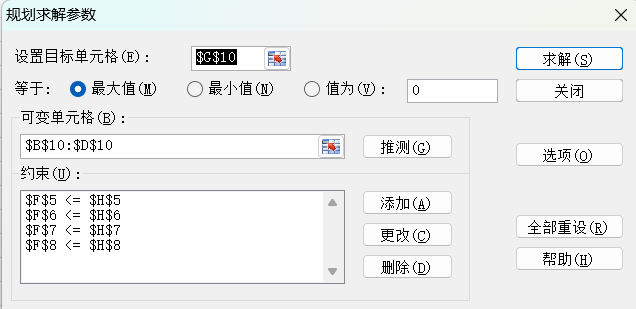
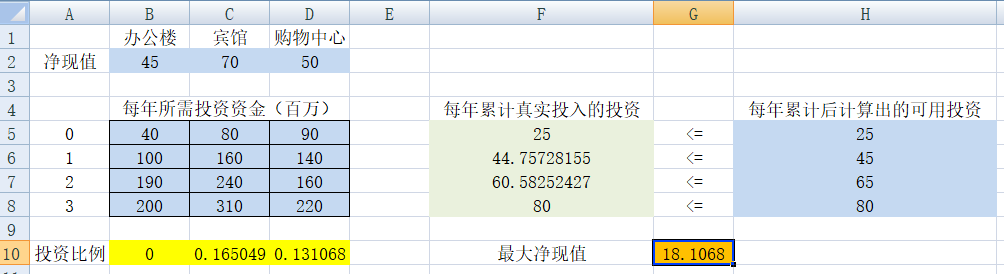
1）输入原始数据和约束条件；

2）对输出值配置等式模式；

• F5=SUMPRODUCT(B5:D5,$B$10:$D$10)
• F6=SUMPRODUCT(B6:D6,$B$10:$D$10)
• F7=SUMPRODUCT(B7:D7,$B$10:$D$10)
• F8=SUMPRODUCT(B8:D8,$B$10:$D$10)
• G10=SUMPRODUCT(B2:D2,B10:D10)

3）规划求解，得到最大净现值。

 

 

资源分配问题总结：

• 资源分配问题，步骤主要如下：

1、确定决策方法，即找到一个度量它某种活动水平的绩效指标，也就是目标函数；

2、明确你有什么资源，每种资源可用的限制是什么，这就是约束条件；

3、根据决策变量输出 中间结果1（绿色表格），进而得到 最终结果（橙色表格）。

• 表格模型，通常都是计算最大利润或者最小成本，约束条件都为≤，因为使用资源不能超过可用资源：

•  通常的难点，都是找到衡量某个水平的决策条件，需要拆解和构造。

 

【网络配送问题示例】目的是，要用最小的成本完成配送，约束形式为 提供的数量=需要的数量。

示例1：

【问题】某公司在2个工厂生产车床。公司现在收到3个顾客的下月订单，要购买车床。

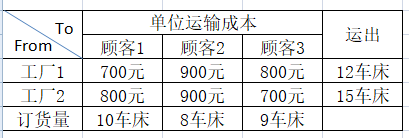
  问，在符合上述供应量的前提下，每个工厂，给每个顾客，运送多少台车床，成本最小？

【求解】

1、双下标问题。设工厂1给顾客1要送X11，工厂1给顾客2要送X12，工厂2给顾客1要送X21，依此类推。则目标函数为，min（总成本）=min（700*X11+900*X12+800*X13+800*X21+900*X22+700*X23）；

2、约束条件：

1）X11+X12+X13=12；

2）X21+X22+X23=15；

3）X11+X21=10；

4）X12+X22=8；

5）X13+X23=9；

6）Xij≥0，i=1,2，j=1,2,3.

3、制作表格，求最优解。

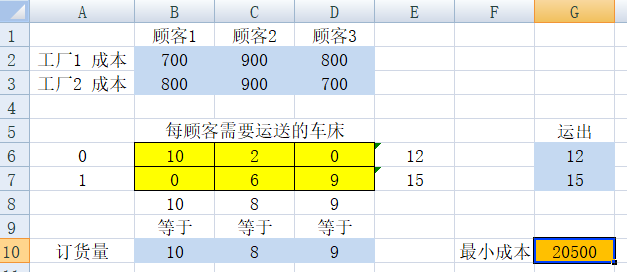
1）蓝色为原始数据，黄色为决策单元，橙色为目标值；

2）等式模型：

• B8=SUM(B6:B7)
• C8=SUM(C6:C7)
• D8=SUM(D6:D7)
• E6=SUM(B6:D6)
• E7=SUM(B7:D7)

3)规划求解。

 

 

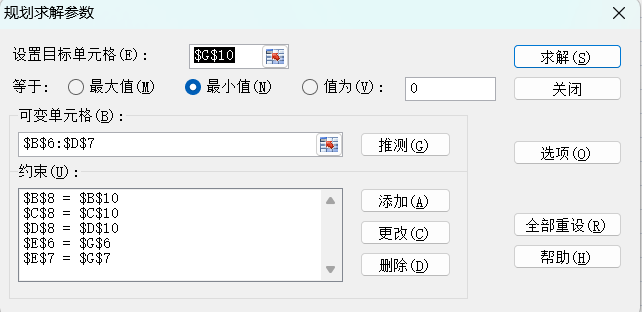
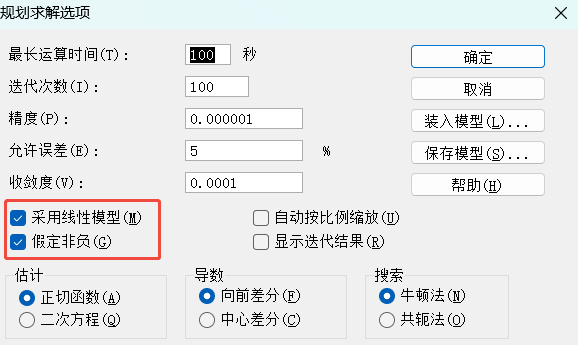
【混合问题示例】资源问题，是小于等于现有资源；收益问题，是大于等于成本或者需要的收益；配送问题，是供货要等于需求量。混合问题，就是结合这三类的情况，以下为具体示例。

示例1：

【问题】某公司经营一个回收中心，从事4种废料的回收，并将回收物处理成可销售的产品（有A，B，C三种产品）。

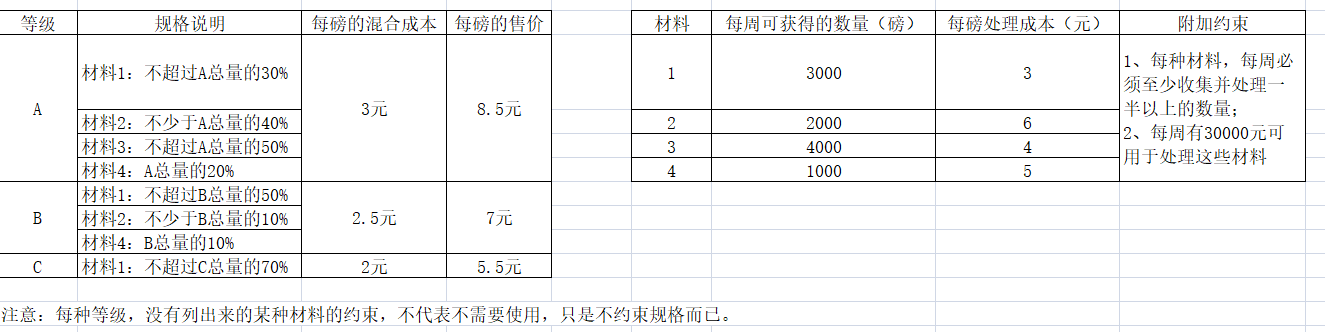
 问，怎么分配材料到不同产品中，获得最大利润？

【求解】

1、决策变量为，每种等级需要的材料。如A需要的材料1重量为A1，材料2为A2，依此类推，得到目标函数max(售价-成本)，即max [(A1+A2+A3+A4)*8.5+(B1+B2+B3+B4)*7+(C1+C2+C3+C4)*5.5-(A1+A2+A3+A4)*3-(B1+B2+B3+B4)*2.5-(C1+C2+C3+C4)*2]，化简后为max [(A1+A2+A3+A4)*5.5+(B1+B2+B3+B4)*4.5+(C1+C2+C3+C4)*3.5]；

2、约束条件为：

• 混合比例的约束

1）A1≤(A1+A2+A3+A4)*30%；

2）A2≥(A1+A2+A3+A4)*40%；

3）A3≤(A1+A2+A3+A4)*50%；

4）A4=(A1+A2+A3+A4)*20%；

5）B1≤(B1+B2+B3+B4)*50%；

6）B2≥(B1+B2+B3+B4)*10%；

7）B4=1000*10%；

8）C1≤(C1+C2+C3+C4)*70%；

• 获得材料及处理的约束

1）3000*50%≤A1+B1+C1≤3000；

2）2000*50%≤A2+B2+C2≤2000；

3）4000*50%≤A3+B3+C3≤4000；

4）1000*50%≤A4+B4+C4≤1000；

5）(A1+B1+C1)*3+(A2+B2+C2)*6+(A3+B3+C3)*4+(A4+B4+C4)*5=30000（这里注意为等号，就是必须要用了这么多钱，不是≤）；

• 所有决策变量做非负性约束

1）Ai，Bi，Ci≥0，i=1,2,3,4.

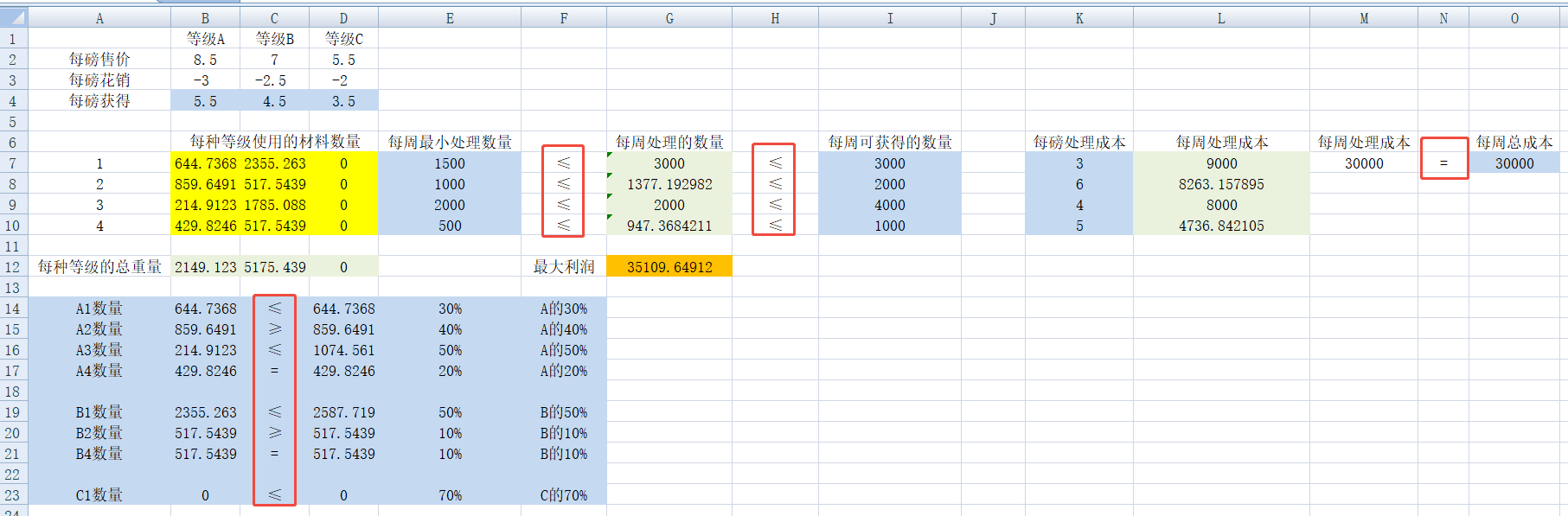
3、制表格，求最优解。红色为约束条件，绿色为输出单元格，黄色为决策变量，橙色为目标格。