线性规划(一)(笔记)
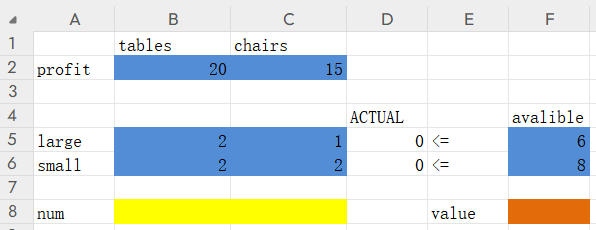
2)定义等式模型:
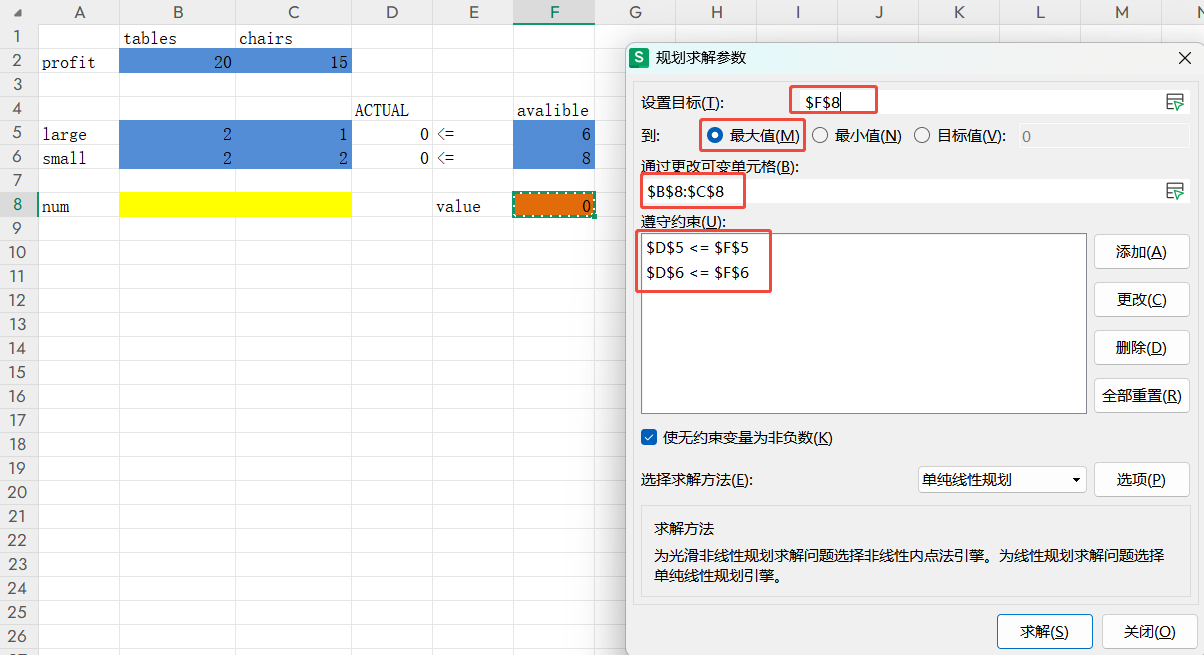
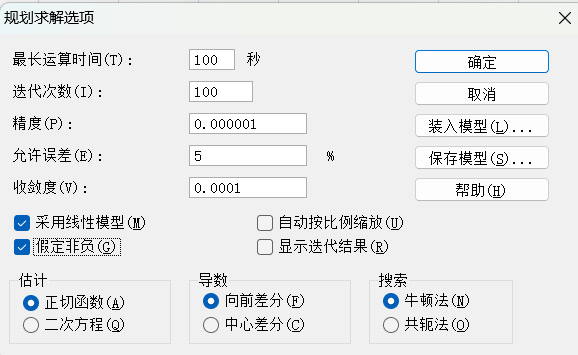
接下来,如果是excel,需要继续点击左边的选项,勾选“采用线性模型”和“假定非负”,来达到x,y≥0的约束。然后点确定,点求解。WPS注意就在当前页,勾选“使无约束变量为非负数”,然后点求解。答案如下,即,最优解为,做2个桌子,2个椅子,可获得最大利润70元:
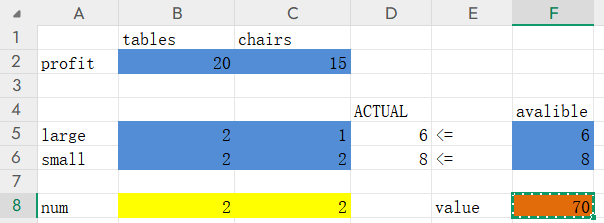
规划最优解示例2:
【问题】
某公司开发两种商品,8英尺的铝框玻璃门和4英尺*6英尺的双把木门窗。公司有三个工厂:
1、工厂1 生产铝框和五金件
2、工厂2 生产木窗
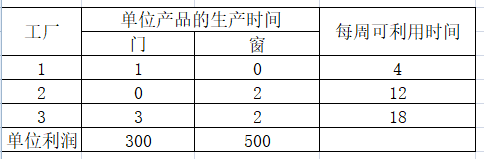
【求解】
1、设门可以制作x个,窗可以制作y个。则目标函数:max(利润)=max(300x+500y);
2、约束条件:
1)工厂1生产的时间=1*x+0*y≤4;
2)工厂2生产的时间=0*x+2*y≤12;
3)工厂3生产的时间=3*x+2*y≤18;
4)x,y≥0
3、这时候,直接将上述三个函数与坐标轴围成一个可行域,然后计算角点的值,即可得到最优解。但我们想用一下excel 2007来练习,下面使用excel 2007来求最优解:
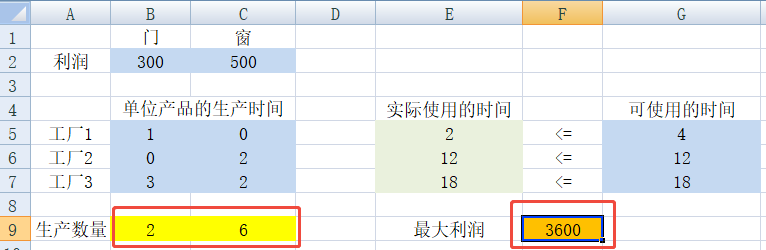
1)根据上述数据,建立一个电子表格。蓝色是原始数据,黄色是决策变量,绿色为根据决策变量输出的内容,橙色是要输出的目标函数:
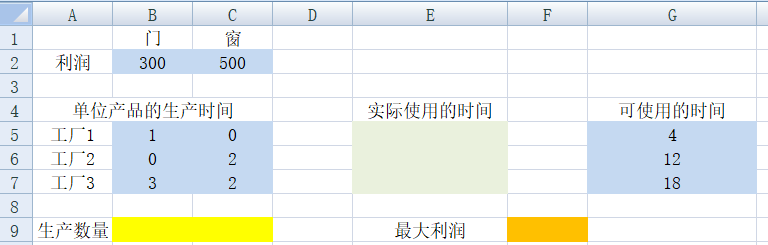
2)为要输出的单元格,定义等式模型:
- E5=SUMPRODUCT(B5:C5,$B$9:$C$9)
- E6=SUMPRODUCT(B6:C6,$B$9:$C$9)
- E7=SUMPRODUCT(B7:C7,$B$9:$C$9)
- F9=SUMPRODUCT(B2:C2,B9:C9)
3)定义约束条件:
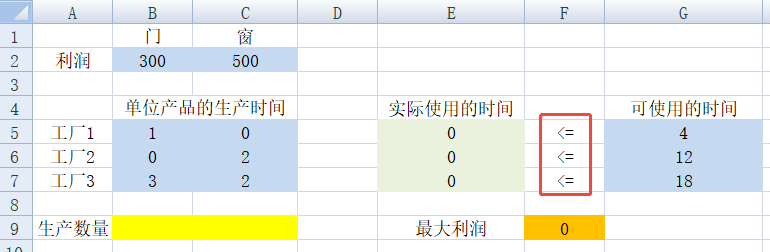
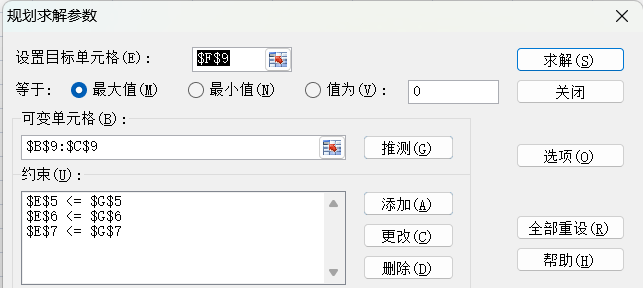
4)计算最优解。鼠标放在目标单元格 F9 上,然后点击“数据--规划求解”,按如下操作:
点击选项,勾选“采用线性模型”和“假定非负”。
点击“求解”,得到最优解,计算完成。
规划最优解示例3:
【问题】某公司决定主要针对三个产品(去污剂、液体洗涤剂、洗衣粉)进行广告宣传,目标是增加它们的销售额。管理部门对每个产品的目标为:
1、去污剂至少增加3%的市场份额;
2、液体洗涤剂至少增加18%的市场份额;
3、洗衣粉至少增加4%的市场份额。
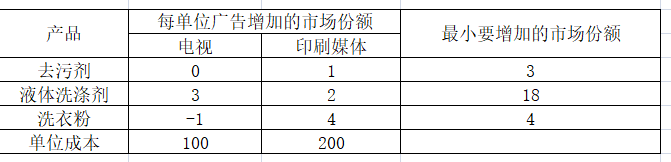
在最低的成本下,达到上述目标,要怎么进行广告投放?
【求解】
1、设电视投放x,印刷媒体投放y。则目标函数为min(成本)=min(100x+200y);
2、约束函数:
1)0*x+1*y≥3;
2)3*x+2*y≥18;
3)(-1)*x+4*y≥4;
4)x,y≥0.
3、利用表格求最优解,即最小成本。
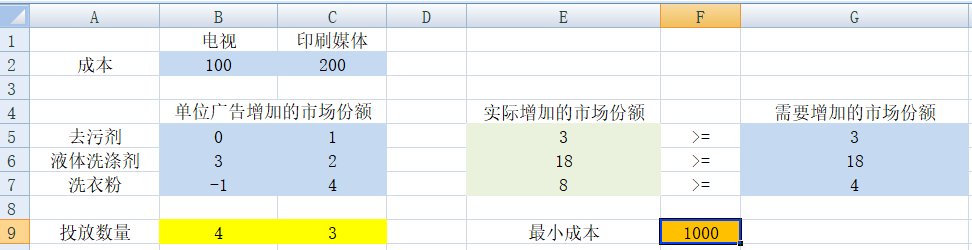
1)根据原始数据建立基础表格。蓝色是原始数据,黄色是决策变量,绿色为根据决策变量输出的内容,橙色是目标函数:

2)添加约束条件:
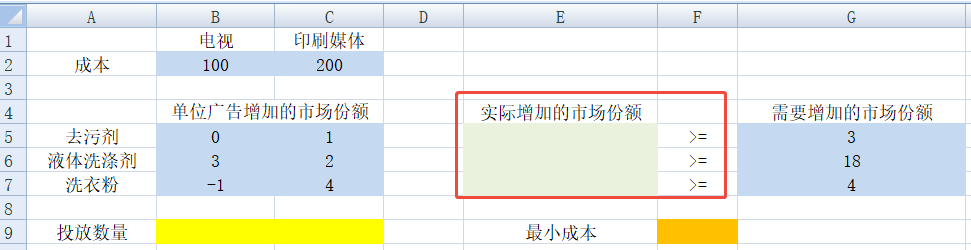
3)为输出单元格,添加等式模型:
- E5=SUMPRODUCT(B5:C5,$B$9:$C$9)
- E6=SUMPRODUCT(B6:C6,$B$9:$C$9)
- E7=SUMPRODUCT(B7:C7,$B$9:$C$9)
- F9=SUMPRODUCT(B2:C2,B9:C9)
4)利用规划求解的宏,计算最优解:
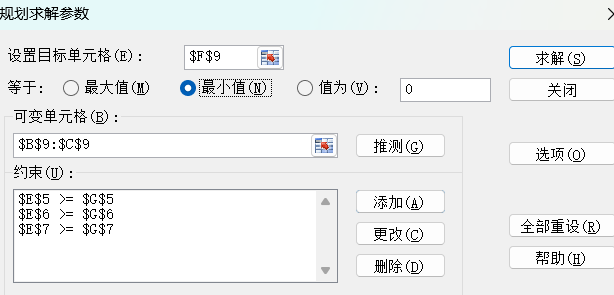
点击“选项”,勾选红框内容。
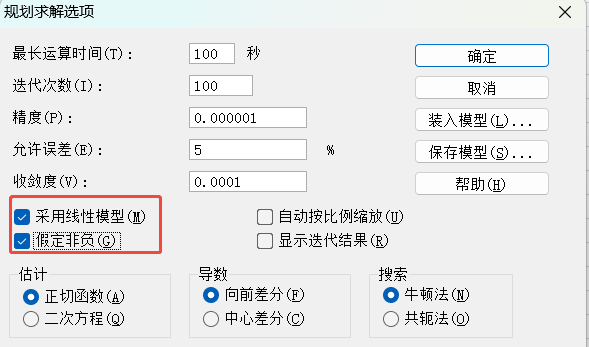
点击“求解”,得到最优解,即最小成本。
规划最优解示例4:
【问题】从甲、乙两地调货,分别供应给A、B、C、D四个物资。具体数据如下。
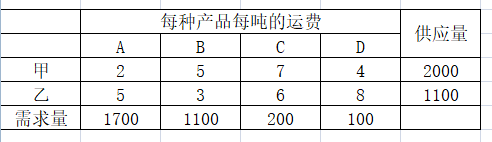
假定运费和运量成正比,试确定总运费最小的调拨方案。
【求解】
1、设甲最终运送的A的吨数为X甲A,设甲最终运送的B的吨数为X甲B,依此类推。但是这种下标不太方便,X甲A就设置为X11,X甲B就设置为X12,以此类推,表格如下:
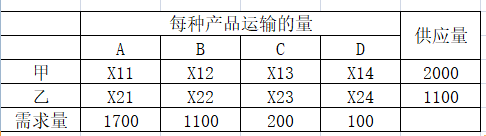
因此,目标函数为:min(运费)=min(2*X11+5*X12+7*X13+4*X14+5*X21+3*X22+6*X23+8*X24);
2、约束函数全部为等式。因为这是供求关系,我要多少,你拿多少给我就行了,不要多,不能少:
1)X11+X12+X13+X14=2000;
2)X21+X22+X23+X24=1100;
3)X11+X21=1700;
4)X12+X22=1100;
5)X13+X23=200;
6)X14+X24=100;
4)Xij≥0,i=1,2,j=1,2,3,4
3、这道题主要是为了学习双下标的建模,不继续计算了。
本文来自博客园,作者:1234roro 当你迷惘的时候,开始学习吧!当你目标清晰的时候,开始学习吧!转载请注明原文链接:https://www.cnblogs.com/1234roro/p/19093438



 浙公网安备 33010602011771号
浙公网安备 33010602011771号