TJ - 「ZJOI2011」道馆之战
「ZJOI2011」道馆之战
难度:2500
\(1s,256MB\)
一,题目:
题目大意:
给你一颗\(n\)个节点的树,每个节点有\(A,B\)两个区域,每个区域可以为障碍物/冰块,只能在冰块上行走,每次行走你可以走到相邻节点的同个区域,或当前节点的另一个区域(前提是这个区域可以走),现在有\(m\)个操作和询问,操作是修改一个节点的两个区域,询问是问你从\(u\)往\(v\)走的路径上,最多经过多少块冰块(不一定要到达\(v\))。
数据范围:
测试点\(1\)~\(6\):\(n≤1000,m≤10000\)
测试点\(7\)~\(15\):\(n≤30000,m≤80000\)
测试点\(16\)~\(20\):\(n≤50000,m≤100000\)
读入格式:
第一行为\(n\)和\(m\)。
第\(2\)行到第\(n\)行,每行包含两个正整数\(x\)和\(y\),表示一条边。
接下来\(n\)行,每行包含两个字符。房间的两个区域,第一个字符为\(A\)区域,第二个字符为\(B\)区域。(“.”是薄冰块,“#”是障碍物)
最后的\(m\)行,每行一个操作:
\(C\) \(u\) \(s\):将房间\(u\)里的两个区域修改为\(s\)。
\(Q\) \(u\) \(v\):从\(u\),往\(v\)走的路径上,最多经过的冰块数。
样例输入:
5 3
1 2
2 3
2 4
1 5
.#
..
#.
.#
..
Q 5 3
C 1 ##
Q 4 5
样例输出:
6
3
二,solution:
首先,这题一眼就是树剖,但是,与一般的题目不同的是,一个节点被分为了两个房间,那么树剖后线段树怎么搞呢?
那么分类讨论就可以了嘛。
我们钦定一个房间编号为\(0\),另一个为\(1\)。用\(1\)表示冰块,\(0\)表示障碍物。
我们树剖后,对于线段树,我们维护这些信息:
\(lans[2]\),表示从这个区间的最左边的节点的\(0/1\)号房间往右走,最多经过的冰块个数(不一定要到达最右边节点,旦不能超过)。
\(rans[2]\),表示从这个区间的最右边的节点的\(0/1\)号房间往右走,最多经过的冰块个数(不一定要到达最左边节点,旦不能超过)。
\(dis[2][2]\)表示从这个区间的最左边的节点的\(0/1\)号房间走到这个区间的最右边的节点的\(0/1\)号房间的最长经过的冰块个数,不能到达的话就为\(-INF\)
首先,新建一个节点的时候好办,直接分类讨论即可:
void make(node &k,int x){//新建一个节点:
//赋初始值
memset(k.lans,0,sizeof(k.lans));
memset(k.rans,0,sizeof(k.rans));
memset(k.dis,-0x3f,sizeof(k.dis));
k.l=k.r=x;//表示这个区间的范围
x=rev[x];
if(a[x][0]==0&&a[x][1]==0) return;//左右房间都是障碍物
else if(a[x][0]==0&&a[x][1]==1){//左房间:障碍物;右房间:冰块
k.lans[1]=k.rans[1]=1;
k.dis[1][1]=1;
}
else if(a[x][0]==1&&a[x][1]==1){//左右房间都是冰块
k.lans[1]=k.rans[1]=k.lans[0]=k.rans[0]=2;
k.dis[0][0]=k.dis[1][1]=1;
k.dis[0][1]=k.dis[1][0]=2;
}
else{//左房间:冰块;右房间:障碍物
k.lans[0]=k.rans[0]=1;
k.dis[0][0]=1;
}
}
合并两个区间要麻烦一点,对于\(lans,rans\)还是类似分类讨论,\(dis\)则利用\(floyd\)的思想(其实还是枚举):
node add(node L,node R){//合并L,R子树
node ans;
//赋初始值
memset(ans.lans,0,sizeof(ans.lans));
memset(ans.rans,0,sizeof(ans.rans));
memset(ans.dis,-0x3f,sizeof(ans.dis));
ans.l=L.l,ans.r=R.r;
for(int i=0;i<=1;i++){
for(int j=0;j<=1;j++){
ans.lans[i]=max(ans.lans[i],max(L.lans[i],L.dis[i][j]+R.lans[j]));
ans.rans[i]=max(ans.rans[i],max(R.rans[i],R.dis[j][i]+L.rans[j]));
for(int k=0;k<=1;k++) ans.dis[i][j]=max(ans.dis[i][j],L.dis[i][k]+R.dis[k][j]);
}
}
return ans;
}
对于修改操作,我们每次直接线段树单点修改,和建树时一样,调用一下\(make\)函数即可。
但是,对于查询操作,就比较恶心的。
首先,这道题是规定了方向的,是从\(u\)往\(v\)走,路径应该这样:

我们查询的时候分类讨论,设\(ans1,ans2\)分别表示从\(u,v\)往\(lca(u,v)\)走的路径上的答案,如下图:
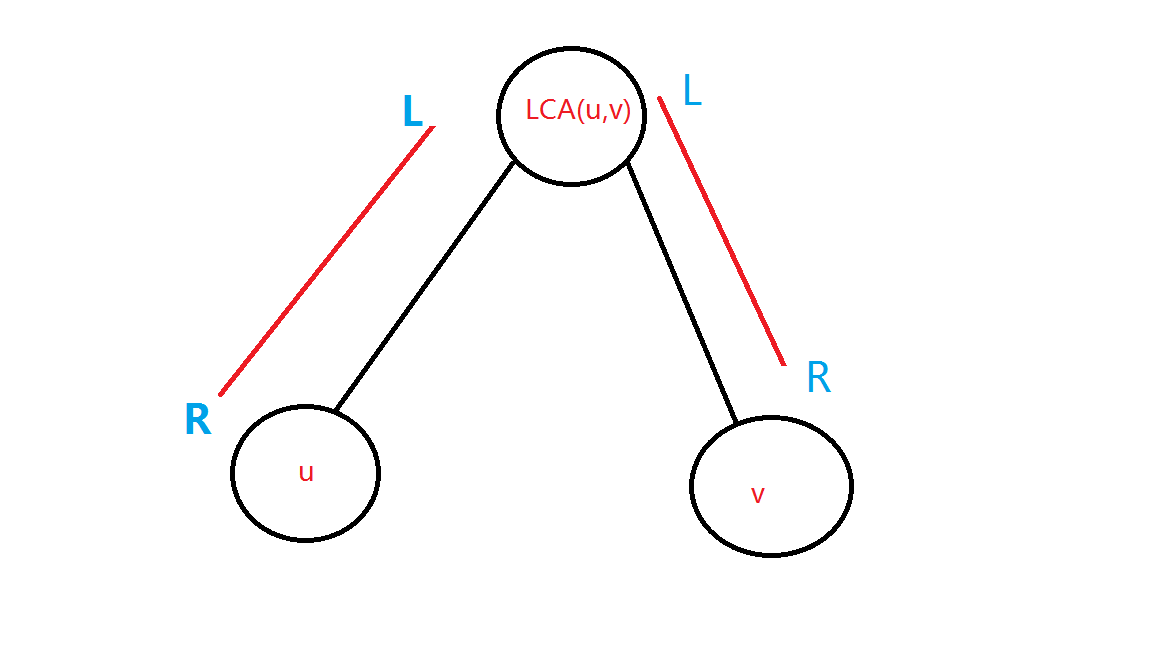
所以,我们需要把\(ans1\)的一些东西翻转一下(\(dis[1][1],dis[0][0]\)没有变化,不用翻转):
swap(ans1.lans[0],ans1.rans[0]);
swap(ans1.lans[1],ans1.rans[1]);
swap(ans1.dis[1][0],ans1.dis[0][1]);
然后把\(ans1,ans2\)合并到\(ans1\),答案就是\(\max\{ans1.lans[0],ans1.lans[1]\}\)
查询的代码:
int solve_2(){//路径查询
int x,y,fx,fy;
scanf("%d%d",&x,&y);
node ans1,ans2;
clean(ans1);clean(ans2);
fx=top[x],fy=top[y];
while(fx!=fy){
if(deep[fx]>deep[fy]){
ans1=add(ask(1,id[fx],id[x]),ans1);
x=fa[fx];fx=top[x];
}
else{
ans2=add(ask(1,id[fy],id[y]),ans2);
y=fa[fy];fy=top[y];
}
}
if(deep[x]>deep[y]){
ans1=add(ask(1,id[y],id[x]),ans1);
}
else{
ans2=add(ask(1,id[x],id[y]),ans2);
}
swap(ans1.lans[0],ans1.rans[0]);
swap(ans1.lans[1],ans1.rans[1]);
swap(ans1.dis[1][0],ans1.dis[0][1]);
ans1=add(ans1,ans2);
return max(ans1.lans[0],ans1.lans[1]);
}
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=50005,INF=0x3f3f3f3f;
int n,m;
//树剖:
vector<int> G[N];
int son[N],siz[N],fa[N],deep[N];
int id[N],rev[N],top[N],dfn;
void dfs1(int x,int dad){
siz[x]=1,fa[x]=dad,deep[x]=deep[dad]+1;
for(auto y : G[x]){
if(y==dad) continue;
dfs1(y,x);
if(siz[son[x]]<siz[y]) son[x]=y;
siz[x]+=siz[y];
}
}
void dfs2(int x){
id[x]=++dfn;rev[dfn]=x;
if(son[x]){
top[son[x]]=top[x];
dfs2(son[x]);
}
for(auto y : G[x]){
if(id[y]) continue;
top[y]=y;
dfs2(y);
}
}
int a[N][2];
struct node{
int l,r;
int lans[2],rans[2],dis[2][2];
}tree[N*4];
void clean(node &x){
memset(x.lans,0,sizeof(x.lans));
memset(x.rans,0,sizeof(x.rans));
memset(x.dis,0,sizeof(x.dis));
}
node add(node L,node R){//合并L,R子树
node ans;
memset(ans.lans,0,sizeof(ans.lans));
memset(ans.rans,0,sizeof(ans.rans));
memset(ans.dis,-0x3f,sizeof(ans.dis));
ans.l=L.l,ans.r=R.r;
for(int i=0;i<=1;i++){
for(int j=0;j<=1;j++){
ans.lans[i]=max(ans.lans[i],max(L.lans[i],L.dis[i][j]+R.lans[j]));
ans.rans[i]=max(ans.rans[i],max(R.rans[i],R.dis[j][i]+L.rans[j]));
for(int k=0;k<=1;k++) ans.dis[i][j]=max(ans.dis[i][j],L.dis[i][k]+R.dis[k][j]);
}
}
return ans;
}
void make(node &k,int x){//新建一个节点:
memset(k.lans,0,sizeof(k.lans));
memset(k.rans,0,sizeof(k.rans));
memset(k.dis,-0x3f,sizeof(k.dis));
k.l=k.r=x;
x=rev[x];
if(a[x][0]==0&&a[x][1]==0) return;
else if(a[x][0]==0&&a[x][1]==1){
k.lans[1]=k.rans[1]=1;
k.dis[1][1]=1;
}
else if(a[x][0]==1&&a[x][1]==1){
k.lans[1]=k.rans[1]=k.lans[0]=k.rans[0]=2;
k.dis[0][0]=k.dis[1][1]=1;
k.dis[0][1]=k.dis[1][0]=2;
}
else{
k.lans[0]=k.rans[0]=1;
k.dis[0][0]=1;
}
}
//线段树模板:
void build(int k,int l,int r){
if(l==r){
make(tree[k],l);
tree[k].l=l,tree[k].r=r;
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);build(k<<1|1,mid+1,r);
tree[k]=add(tree[k<<1],tree[k<<1|1]);
}
void change(int k,int x){
if(tree[k].l==tree[k].r&&tree[k].l==x){
make(tree[k],x);
return;
}
if(x<=tree[k<<1].r) change(k<<1,x);
else change(k<<1|1,x);
tree[k]=add(tree[k<<1],tree[k<<1|1]);
}
node ask(int k,int x,int y){
if(x<=tree[k].l&&tree[k].r<=y) return tree[k];
if(y<=tree[k<<1].r) return ask(k<<1,x,y);
if(x>=tree[k<<1|1].l) return ask(k<<1|1,x,y);
return add(ask(k<<1,x,y),ask(k<<1|1,x,y));
}
void solve_1(){//单点修改
int x;char ch1,ch2;
cin>>x>>ch1>>ch2;
a[x][0]=(ch1=='.');
a[x][1]=(ch2=='.');
change(1,id[x]);
}
int solve_2(){//路径查询
int x,y,fx,fy;
scanf("%d%d",&x,&y);
node ans1,ans2;
//ans1表示从x<-lca(x,y),ans2表示y<-lca(x,y),一开始他们都为0
clean(ans1);clean(ans2);
fx=top[x],fy=top[y];
//由于有方向上的区别,需要分类讨论:
while(fx!=fy){
if(deep[fx]>deep[fy]){
ans1=add(ask(1,id[fx],id[x]),ans1);
x=fa[fx];fx=top[x];
}
else{
ans2=add(ask(1,id[fy],id[y]),ans2);
y=fa[fy];fy=top[y];
}
}
if(deep[x]>deep[y]){
ans1=add(ask(1,id[y],id[x]),ans1);
}
else{
ans2=add(ask(1,id[x],id[y]),ans2);
}
//交换,使得ans1表示x->lca(x,y)
swap(ans1.lans[0],ans1.rans[0]);
swap(ans1.lans[1],ans1.rans[1]);
swap(ans1.dis[1][0],ans1.dis[0][1]);
ans1=add(ans1,ans2);//合并
return max(ans1.lans[0],ans1.lans[1]);
}
int main(){
scanf("%d%d",&n,&m);
int x,y;
for(int i=1;i<n;i++){
scanf("%d%d",&x,&y);
G[x].push_back(y);
G[y].push_back(x);
}
//树剖:
dfs1(1,0);
top[1]=1;
dfs2(1);
char ch1,ch2;
for(int i=1;i<=n;i++){
cin>>ch1>>ch2;
a[i][0]=(ch1=='.');
a[i][1]=(ch2=='.');
}
//建立线段树:
build(1,1,n);
char opt;
while(m--){
cin>>opt;
if(opt=='C') solve_1();
else printf("%d\n",solve_2());
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号